Ecuación de una hipérbola a partir de su excentricidad y de un foco
Para determinar la ecuación de una hipérbola con centro en el origen, conociendo su excentricidad y las coordenadas de uno de sus focos, se procede del siguiente modo:
- Si el foco se encuentra sobre el eje x, la ecuación de la hipérbola es: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ y la excentricidad se define como $ e = \frac{c}{a} $.
- Si el foco está ubicado sobre el eje y, la ecuación correspondiente es: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$ y la excentricidad se expresa como $ e = \frac{c}{b} $.
La relación que vincula los semiejes con la distancia del centro a los focos viene dada por la fórmula: $$ c^2 = a^2 + b^2 $$
Resolviendo este sistema de ecuaciones, se obtienen los valores de los semiejes $ a $ y $ b $, necesarios para escribir la ecuación de la hipérbola.
Ejemplo práctico
Supongamos una hipérbola con centro en el origen, foco en $ F(3, 0) $ y excentricidad $ e = \frac{3}{2} $.
Dado que el foco se encuentra sobre el eje x, la ecuación adopta la forma:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
En este caso, la excentricidad está definida por:
$$ e = \frac{c}{a} $$
Podemos plantear el siguiente sistema:
$$ \begin{cases} e = \frac{c}{a} \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \end{cases} $$
Como $ e = \frac{3}{2} $ y el foco es $ F(c, 0) = (3, 0) $, tenemos $ c = 3 $. Sustituyendo:
$$ \begin{cases} \frac{3}{2} = \frac{3}{a} \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \end{cases} $$
De la primera ecuación se deduce directamente:
$$ a = 2 $$
Por lo tanto, el vértice real sobre el eje x se encuentra en $ A(a, 0) = (2, 0) $.
Conocido $ a $, podemos determinar $ b $ aplicando la relación fundamental:
$$ c^2 = a^2 + b^2 $$
Con $ c = 3 $ y $ a = 2 $:
$$ 9 = 4 + b^2 $$
$$ b^2 = 5 $$
$$ b = \sqrt{5} $$
Ahora sustituimos los valores obtenidos en la ecuación estándar de la hipérbola:
$$ \frac{x^2}{4} - \frac{y^2}{5} = 1 $$
Esta es la ecuación de la hipérbola centrada en el origen, con foco en $ F(3, 0) $ y excentricidad $ e = \frac{3}{2} $.
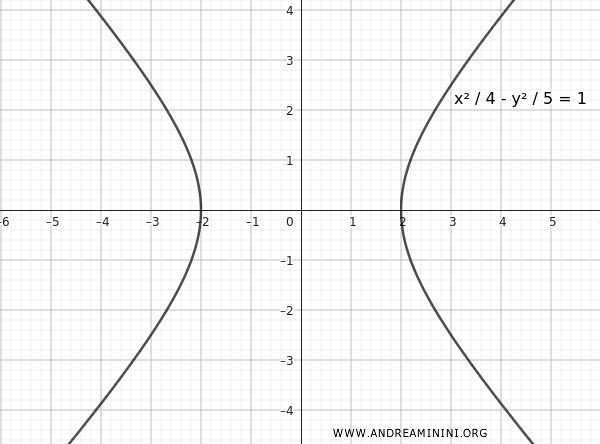
Así se obtiene la ecuación buscada.