Rectas tangentes a una hipérbola

Para determinar las rectas tangentes a una hipérbola que pasan por un punto $ P(x₀, y₀) $, se plantea un sistema formado por la ecuación de la hipérbola y la de la familia de rectas que pasan por el punto $ P $.

$$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \\ \\ y - y_0 = m(x - x_0) \end{cases} $$

Este sistema nos permite obtener una ecuación cuadrática en la variable $ y $.

Para encontrar las rectas tangentes, imponemos la condición de tangencia $ \Delta = 0 $ sobre dicha ecuación cuadrática y resolvemos respecto a la pendiente $ m $.

Si la ecuación tiene dos soluciones reales distintas $ m_1 \ne m_2 $, existen dos tangentes a la hipérbola que pasan por el punto $ P(x_0, y_0) $, lo que implica que el punto se encuentra fuera de la hipérbola.
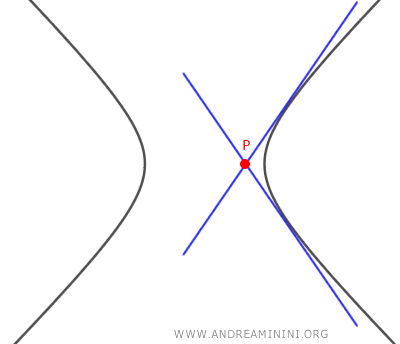
Si la ecuación tiene una única solución real $ m_1 = m_2 $, hay una sola tangente que pasa por el punto $ P(x_0, y_0) $, lo cual significa que dicho punto pertenece a la hipérbola.
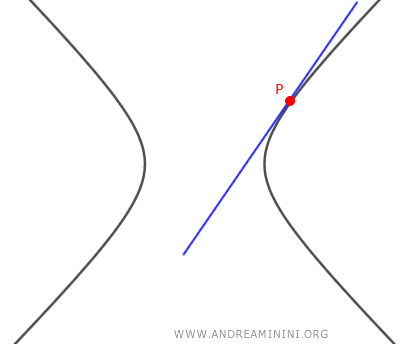
Si no existen soluciones reales, entonces no hay ninguna tangente a la hipérbola que pase por el punto $ P(x_0, y_0) $.

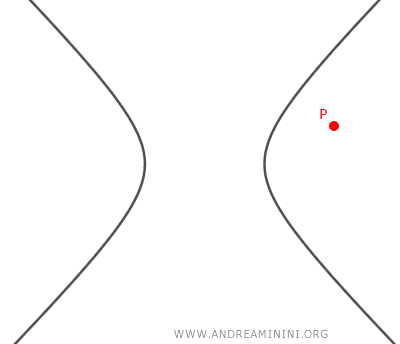
Ejemplo práctico

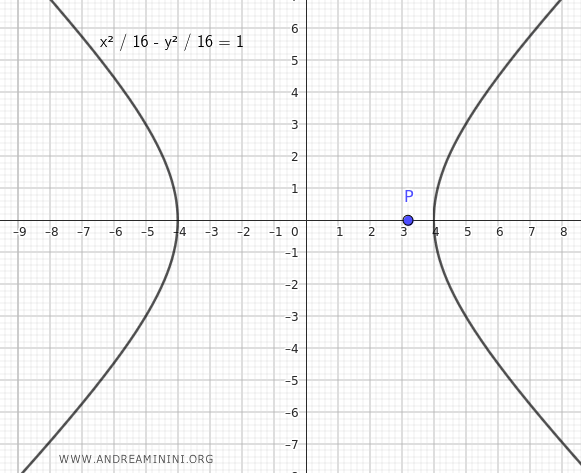
Consideremos la hipérbola:

$$ \frac{x^2}{16} - \frac{y^2}{16} = 1 $$

Queremos determinar las rectas tangentes que pasan por el punto $ P\left( \frac{16}{5}, 0 \right) $.

Ejemplo

Planteamos el sistema formado por la ecuación de la hipérbola y la de la familia de rectas que pasan por $ P\left( \frac{16}{5}, 0 \right) $:

$$ \begin{cases} \frac{x^2}{16} - \frac{y^2}{16} = 1 \\ \\ y - y_0 = m(x - x_0) \end{cases} $$

Donde $ x_0 = \frac{16}{5} $ y $ y_0 = 0 $:

$$ \begin{cases} \frac{x^2}{16} - \frac{y^2}{16} = 1 \\ \\ y = mx - \frac{16m}{5} \end{cases} $$

Sustituimos la expresión de $ y $ en la ecuación de la hipérbola:

$$ y^2 = x^2 - 16 $$

$$ y = mx - \frac{16m}{5} $$

Igualamos ambas expresiones de $ y $:

$$ \sqrt{x^2 - 16} = mx - \frac{16m}{5} $$

Elevamos al cuadrado ambos miembros:

$$ x^2 - 16 = m^2x^2 - \frac{32m^2x}{5} + \frac{256m^2}{25} $$

Reordenamos los términos para obtener una ecuación cuadrática en $ x $:

$$ x^2(1 - m^2) + x \cdot \frac{32m^2}{5} - 16 - \frac{256m^2}{25} = 0 $$

Aplicamos la condición de tangencia:

$$ \Delta = b^2 - 4ac = 0 $$

Con $ a = 1 - m^2 $, $ b = \frac{32m^2}{5} $ y $ c = -16 - \frac{256m^2}{25} $, se obtiene:

$$ \left( \frac{32m^2}{5} \right)^2 - 4(1 - m^2)\left(-16 - \frac{256m^2}{25} \right) = 0 $$

$$ \frac{1024m^4}{25} + 64 + \frac{1024m^2}{25} - 64m^2 = 0 $$

$$ \frac{1024m^2 - 1600m^2}{25} + 64 = 0 $$

$$ -\frac{576m^2}{25} = -64 $$

$$ m^2 = \frac{64 \cdot 25}{576} = \frac{1600}{576} = \frac{25}{9} $$

$$ m = \pm \frac{5}{3} $$

Conocidas las pendientes, las sustituimos en la ecuación de la recta:

$$ y = mx - \frac{16m}{5} $$

Para $ m = \frac{5}{3} $:
$$ y = \frac{5}{3}x - \frac{80}{15} = \frac{5}{3}x - \frac{16}{3} $$
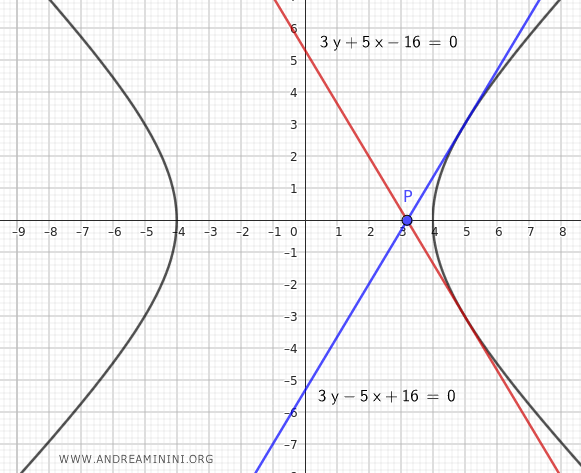
$$ 3y - 5x + 16 = 0 $$
Para $ m = -\frac{5}{3} $:
$$ y = -\frac{5}{3}x + \frac{80}{15} = -\frac{5}{3}x + \frac{16}{3} $$
$$ 3y + 5x - 16 = 0 $$

A continuación, se muestra el gráfico de las rectas tangentes a la hipérbola que pasan por el punto $ P\left( \frac{16}{5}, 0 \right) $:

Gráfico

Y así sucesivamente.