Ecuación de una hipérbola dados un vértice y un foco
Para determinar la ecuación de una hipérbola centrada en el origen, a partir de las coordenadas de un vértice y de un foco, basta con seguir los siguientes pasos:
- Si el foco \((c, 0)\) y el vértice \((a, 0)\) se encuentran sobre el eje \(x\), la ecuación es:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ En cambio, si el foco \((0, c)\) y el vértice \((0, b)\) están sobre el eje \(y\), la ecuación correspondiente es:
$$ \frac{y^2}{a^2} - \frac{x^2}{b^2} = 1 $$ - Calcula \(b\) a partir de la relación entre los parámetros \(a\), \(b\) y \(c\): $$ c^2 = a^2 + b^2 $$
Una vez conocidas las longitudes de los semiejes \(a\) (transverso) y \(b\) (conjugado), ya se puede escribir la ecuación de la hipérbola.
Ejemplo
Considera una hipérbola centrada en el origen \( O(0,0) \), con un foco en \(F(5, 0)\) y un vértice en \(A(3, 0)\).
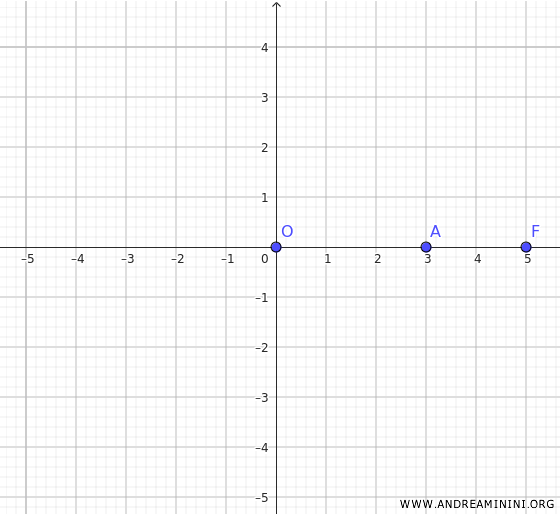
Como los focos se encuentran sobre el eje \(x\), la ecuación de la hipérbola es:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
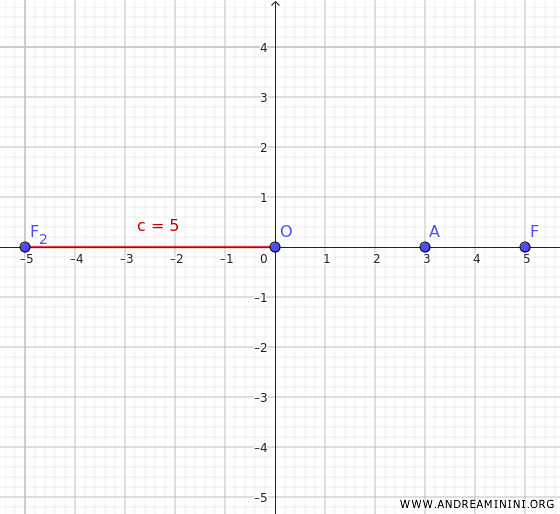
La hipérbola es simétrica respecto a su centro y a los ejes coordenados. Por tanto, si uno de los focos está en \(F(5, 0)\), el otro debe encontrarse en \(F_2(-5, 0)\).
En ambos casos, la distancia entre el centro y un foco es \( c = 5 \).
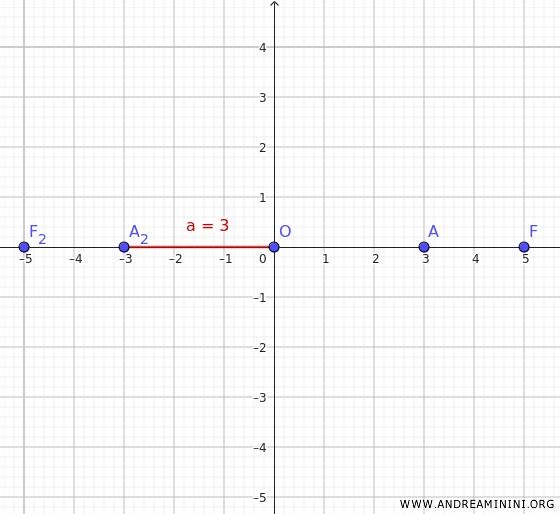
De forma análoga, si uno de los vértices está en \(A(3, 0)\), el otro se sitúa en \(A_2(-3, 0)\).
La distancia del centro a cada vértice es, por tanto, \( a = 3 \).
A continuación, usamos la relación fundamental para calcular el valor de \( b \), asociado al semieje conjugado:
$$ c^2 = a^2 + b^2 $$
$$ 5^2 = 3^2 + b^2 $$
$$ 25 = 9 + b^2 $$
$$ b^2 = 25 - 9 $$
$$ b^2 = 16 $$
$$ \sqrt{b^2} = \sqrt{16} $$
$$ b = \pm 4 $$
Como \(b\) representa una longitud, se considera únicamente el valor positivo:
$$ b = 4 $$
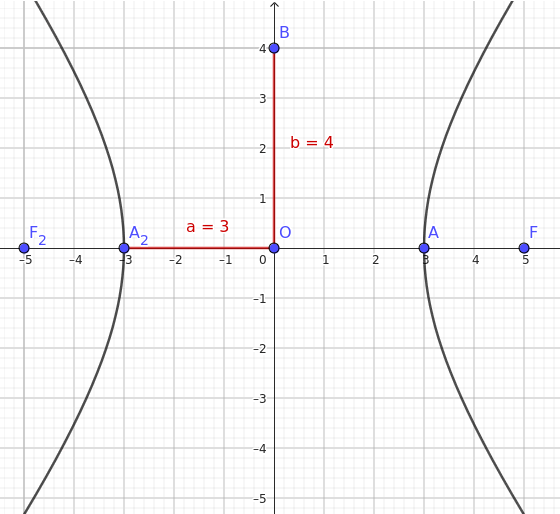
Con los valores \( a = 3 \) y \( b = 4 \), ya podemos escribir la ecuación de la hipérbola:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
Sustituyendo los valores numéricos:
$$ \frac{x^2}{3^2} - \frac{y^2}{4^2} = 1 $$
$$ \frac{x^2}{9} - \frac{y^2}{16} = 1 $$
En conclusión, la ecuación de la hipérbola centrada en el origen, con un foco en \((5, 0)\) y un vértice en \((3, 0)\), es:
\( \frac{x^2}{9} - \frac{y^2}{16} = 1 \).
Y así sucesivamente.