Ecuación de una hipérbola a partir de un asíntota y un punto
Para determinar la ecuación de una hipérbola con centro en el origen, conociendo la ecuación de uno de sus asíntotas $ y = \frac{b}{a} x $ y las coordenadas de un punto $ P(x_0;y_0) $ que pertenece a la curva, se procede del siguiente modo:
En primer lugar, es necesario identificar el eje transverso - es decir, el eje sobre el que se encuentran los focos - para poder elegir la forma canónica adecuada de la ecuación de la hipérbola:
- Si el eje transverso es el eje x, la ecuación será: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
- Si el eje transverso es el eje y, la ecuación será: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
A continuación, se plantea un sistema de ecuaciones combinando la forma canónica de la hipérbola con la ecuación del asíntota:
$$ \begin{cases} y = \pm \frac{b}{a} x \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \end{cases} $$
Luego, se sustituyen $ x $ e $ y $ por las coordenadas del punto conocido $ P(x_0;y_0) $ en la ecuación de la hipérbola:
$$ \begin{cases} y = \pm \frac{b}{a} x \\ \\ \frac{x_0^2}{a^2} - \frac{y_0^2}{b^2} = \pm 1 \end{cases} $$
Al resolver este sistema, se obtienen los valores de los semiejes $ a $ y $ b $, lo que permite escribir la ecuación completa de la hipérbola.
Un ejemplo práctico
Vamos a determinar la ecuación de una hipérbola con centro en el origen, focos sobre el eje x, que pasa por el punto $ P\left( - \frac{5}{2}, -1 \right) $ y tiene como asíntota la recta $ y = \frac{2}{\sqrt{5}} x $.
Dado que los focos se encuentran sobre el eje x, la ecuación tendrá la forma:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
Sustituimos las coordenadas del punto $ P\left( - \frac{5}{2}, -1 \right) $ en dicha expresión:
$$ \frac{\left( - \frac{5}{2} \right)^2}{a^2} - \frac{(-1)^2}{b^2} = 1 $$
$$ \frac{\frac{25}{4}}{a^2} - \frac{1}{b^2} = 1 $$
$$ \frac{25}{4a^2} - \frac{1}{b^2} = 1 $$
Ahora, planteamos un sistema utilizando esta ecuación junto con la del asíntota:
$$ \begin{cases} y = \frac{2}{\sqrt{5}} x \\ \\ \frac{25}{4a^2} - \frac{1}{b^2} = 1 \end{cases} $$
Recordando que el asíntota tiene la forma $ y = \frac{b}{a} x $, igualamos los coeficientes de $ x $:
$$ \begin{cases} \frac{b}{a} = \frac{2}{\sqrt{5}} \\ \\ \frac{25}{4a^2} - \frac{1}{b^2} = 1 \end{cases} $$
De la primera ecuación despejamos $ b $:
$$ \begin{cases} b = \frac{2}{\sqrt{5}} a \\ \\ \frac{25}{4a^2} - \frac{1}{b^2} = 1 \end{cases} $$
Sustituimos esta expresión de $ b $ en la segunda ecuación:
$$ \frac{25}{4a^2} - \frac{1}{\left( \frac{2}{\sqrt{5}} a \right)^2} = 1 $$
Calculamos el cuadrado del denominador:
$$ \frac{25}{4a^2} - \frac{1}{\frac{4a^2}{5}} = 1 $$
$$ \frac{25}{4a^2} - \frac{5}{4a^2} = 1 $$
$$ \frac{25 - 5}{4a^2} = 1 $$
$$ \frac{20}{4a^2} = 1 $$
$$ \frac{5}{a^2} = 1 $$
De aquí se obtiene:
$$ a^2 = 5 $$
$$ a = \sqrt{5} $$
Volvemos a la expresión $ b = \frac{2}{\sqrt{5}} a $ para calcular $ b $:
$$ b = \frac{2}{\sqrt{5}} \cdot \sqrt{5} = 2 $$
Conocidos los valores $ a = \sqrt{5} $ y $ b = 2 $, ya podemos escribir la ecuación de la hipérbola:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{(\sqrt{5})^2} - \frac{y^2}{2^2} = 1 $$
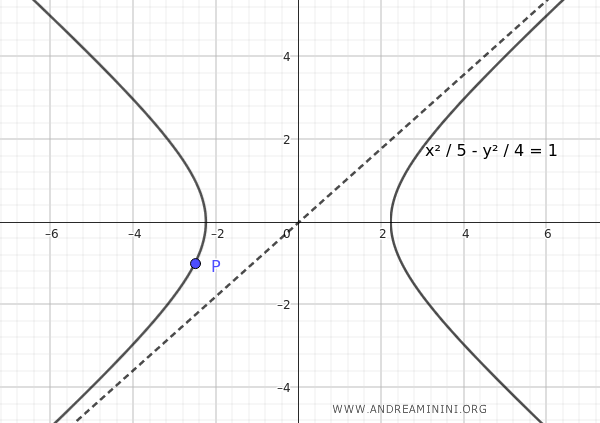
$$ \frac{x^2}{5} - \frac{y^2}{4} = 1 $$
Esta es, por tanto, la ecuación de la hipérbola con centro en el origen, eje focal sobre el eje x, que pasa por el punto $ P\left( - \frac{5}{2}, -1 \right) $ y cuya asíntota es $ y = \frac{2}{\sqrt{5}} x $.
Y así continúa el procedimiento.