Hipérbola
Una hipérbola es una curva plana definida como el lugar geométrico de los puntos P cuya diferencia absoluta de distancias a dos puntos fijos, F1 y F2, llamados focos, permanece constante (2a). $$ | \overline{PF}_1 - \overline{PF}_2 | = 2a $$ donde 2a representa la distancia entre los dos vértices de la hipérbola.
La hipérbola es una curva abierta compuesta por dos ramas que se extienden indefinidamente siguiendo la dirección de dos rectas oblicuas denominadas asíntotas.
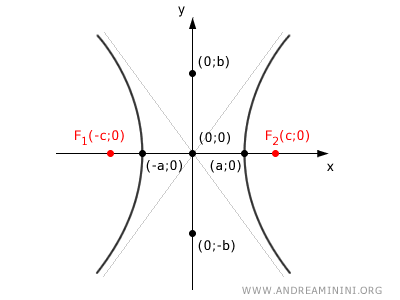
Los vértices de la hipérbola, situados en (-a;0) y (a;0), están separados por una distancia de 2a.
La distancia entre cada vértice y el centro de la hipérbola es igual a "a".
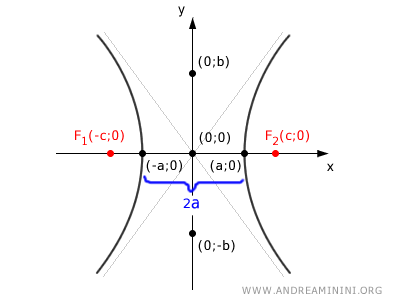
Si se consideran dos puntos cualesquiera P1 y P2 sobre la hipérbola, la diferencia absoluta entre sus distancias a los focos será siempre la misma.
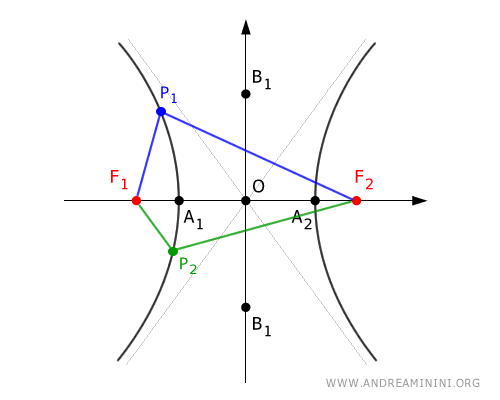
Dicho de otro modo, cualquier par de puntos sobre la hipérbola cumple con la siguiente relación:
$$ | \overline{P_1F_1} - \overline{P_1F_2} | = | \overline{P_2F_1} - \overline{P_2F_2} | $$
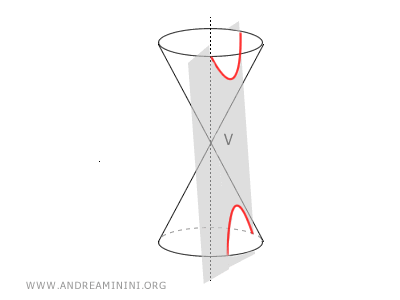
Nota: La hipérbola es una sección cónica, ya que se puede obtener al intersectar un cono circular con un plano cuyo ángulo de inclinación es menor que el ángulo de apertura del cono.
Características
Una hipérbola es el conjunto de puntos del plano cuya diferencia de distancias respecto a dos puntos fijos, F1 y F2, llamados focos, se mantiene constante.
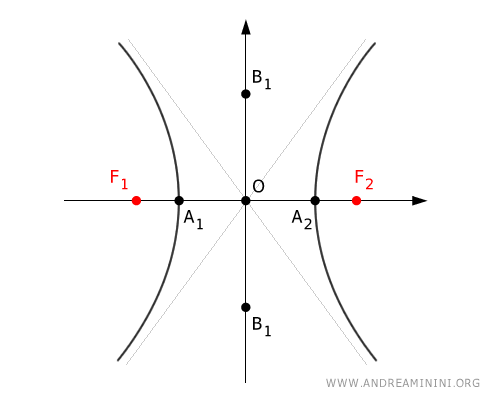
La recta que une los focos F1 y F2 se denomina eje principal (o eje transverso).
Los puntos de intersección A1 y A2 entre la hipérbola y el eje principal se denominan vértices reales.
Nota: En algunos textos, el término "eje transverso" se emplea también para referirse al segmento que une los vértices reales A1 y A2, cuya longitud es siempre 2a. $$ \overline{A_1A_2} = 2a $$ En ese caso, se llama semieje transverso a la distancia "a" entre un vértice y el centro O de la hipérbola. $$ \overline{OA_1} = \overline{OA_2} = a $$
El segmento F1F2 se conoce como eje secundario (o eje conjugado).
Los puntos B1 y B2, situados sobre dicho eje, se denominan vértices imaginarios, ya que no pertenecen a la curva, pero permiten determinar la pendiente de las asíntotas.
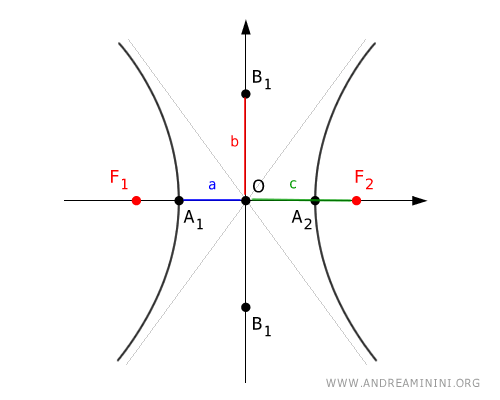
El punto O, intersección de los ejes principal y secundario, se denomina centro de la hipérbola.
Este punto O es el punto medio del segmento \overline{F_1F_2} que une los focos.
En el esquema, las letras "a", "b" y "c" representan, respectivamente, las distancias desde el centro O hasta los vértices reales, los vértices imaginarios y los focos.
Las asíntotas son rectas oblicuas que pasan por el centro O de la hipérbola y que se aproximan a sus ramas en el infinito.
La distancia entre los focos $ F_1 $ y $ F_2 $ se denomina distancia focal.
$$ 2c = \overline{F_1F_2} $$
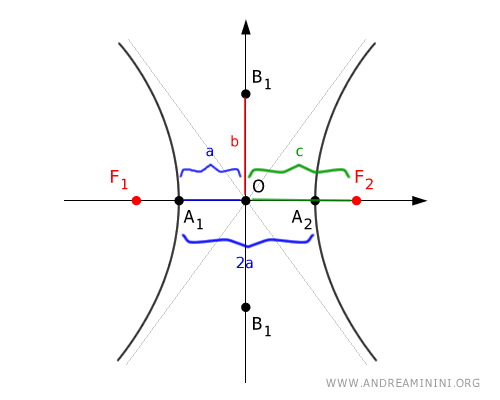
Para cualquier punto $ P $ sobre la hipérbola, la diferencia absoluta entre las distancias $ | \overline{PF}_1 - \overline{PF}_2 | $ es constante e igual a $ 2a $
$$ | \overline{PF}_1 - \overline{PF}_2 | = 2a $$
Los puntos $ P $, $ F_1 $ y $ F_2 $ determinan un triángulo $ PF_1F_2 $, cuyo lado más largo es siempre $ \overline{F_1F_2} = 2c $.
La diferencia entre los otros dos lados del triángulo es $ | \overline{PF}_1 - \overline{PF}_2 | = 2a $
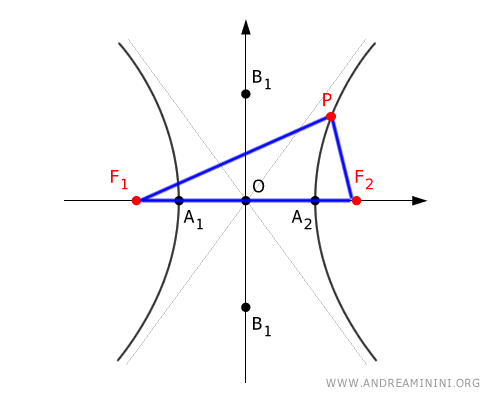
De acuerdo con el teorema de la desigualdad triangular, en cualquier triángulo, un lado es siempre mayor que la diferencia de los otros dos, por lo que 2c > 2a
$$ 2c > 2a $$
de donde se deduce que
$$ c > a $$
Por tanto, en toda hipérbola, la distancia $ c $ desde un foco hasta el centro $ O $ es mayor que la distancia entre un vértice y el centro.
Ecuación Canónica de la Hipérbola
Para representar una hipérbola, se utiliza habitualmente un sistema de coordenadas cartesianas donde:
- el centro de la hipérbola coincide con el origen O(0;0)
- el eje principal de la hipérbola, que une los focos F1 y F2, se alinea con el eje x o con el eje y.
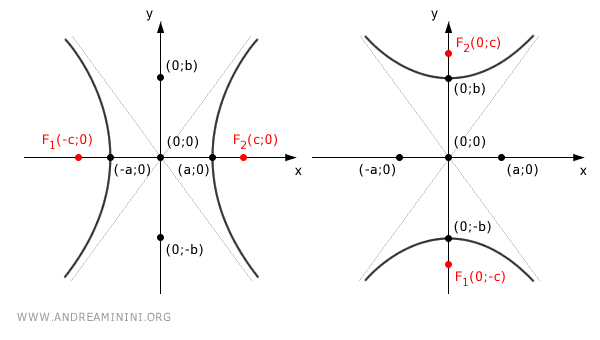
Esta configuración permite emplear la ecuación canónica de la hipérbola.
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 $$
Donde "a" y "b" representan las semidistancias entre los vértices.
- Si el eje principal es el eje x, la constante de la ecuación canónica es +1 $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
- Si el eje principal es el eje y, dicha constante es -1 $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
En resumen, si los focos F1 y F2 están sobre el eje x, la constante es +1; si están sobre el eje y, es -1.
También puede utilizarse la forma explícita de la ecuación de la hipérbola.
$$ y = \pm \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}-1 ) } \ \ \ \ \text{focos sobre el eje x}$$
$$ y = \pm \sqrt{ b^2 \cdot ( \frac{x^2}{a^2}+1 ) } \ \ \ \ \text{focos sobre el eje y}$$
Según el eje elegido, las coordenadas de los focos de la hipérbola son:
- Si el eje principal es el eje x: $$ F_1(-c;0 ) $$ $$ F_2(c;0 ) $$
- Si el eje principal es el eje y: $$ F_1(0;-c ) $$ $$ F_2(0;c ) $$
Donde "c" es la distancia desde los focos hasta el centro.
$$ c = \sqrt{a^2+b^2} $$
Nota: Si el eje principal es el eje x, siempre se cumple que c > a. En cambio, si el eje principal es el eje y, se cumple que c > b.
Las asíntotas de la hipérbola están dadas por las siguientes ecuaciones:
$$ y = \pm \frac{b}{a} x $$
En este caso simplificado, las asíntotas siempre pasan por el origen O(0;0) y por los puntos (a;b) y (a;-b).
Finalmente, la excentricidad (e) de la hipérbola se define como el cociente entre la distancia de los focos (c) y la de los vértices reales (a) al centro.
$$ e = \frac{c}{a} $$
A mayor valor de "e", más abiertas están las ramas de la curva.
Nota: A diferencia de la elipse, la excentricidad de una hipérbola es siempre mayor que 1, es decir, e > 1, porque la distancia de los focos al centro siempre supera la de los vértices.
Toda hipérbola posee dos focos y dos rectas directrices, simétricas y perpendiculares al eje transverso.
Si el eje transverso coincide con el eje x, las rectas directrices son:
$$ x = \pm \frac{a^2}{c} $$
Si el eje transverso es el eje y, las rectas directrices se expresan como:
$$ y = \pm \frac{b^2}{c} $$
En general, como en toda sección cónica, para un punto dado $ P(x;y) $ sobre la hipérbola, el cociente entre la distancia $ \overline{PF} $ al foco y la distancia $ \overline{PH} $ a la directriz es constante e igual a la excentricidad (e).
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
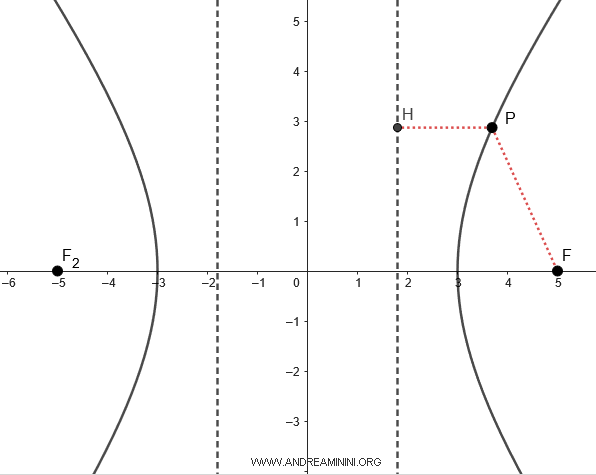
Un Ejemplo Práctico
Analicemos una hipérbola cuyos focos se encuentran sobre el eje x, con centro en el origen del sistema cartesiano O(0;0), y con parámetros a=3 y b=4.
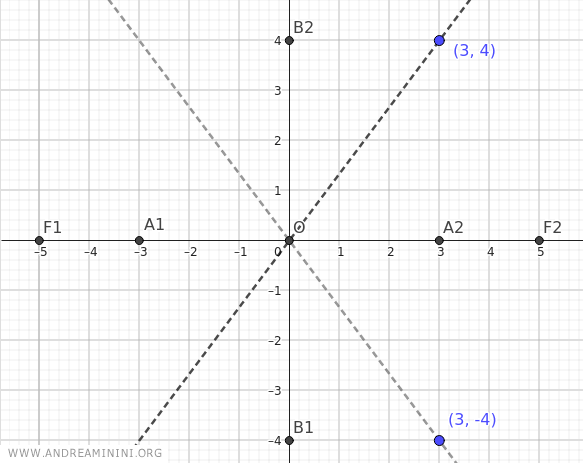
Comenzamos identificando los puntos (a;b)=(3;4) y (a;-b)=(3;-4).
Luego trazamos las rectas que pasan por el centro de la hipérbola y por los puntos (3;4) y (3;-4).
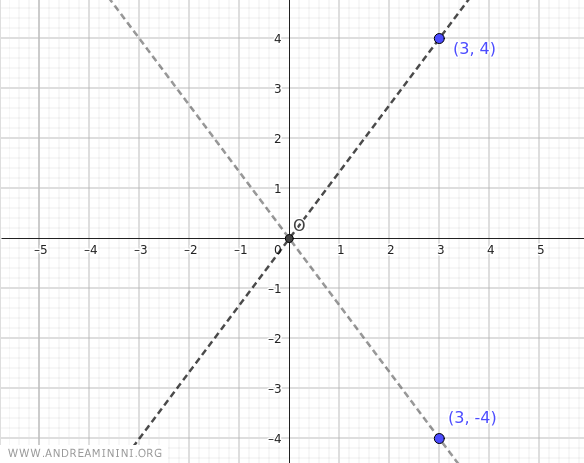
Así se obtienen las asíntotas de la hipérbola.
Otra forma de determinar las asíntotas consiste en utilizar su ecuación explícita:
$$ y = \pm \frac{b}{a} \cdot x $$
Sustituyendo a=3 y b=4, se tiene:
$$ y = \pm \frac{4}{3} \cdot x $$
Una vez trazadas las asíntotas, determinamos los vértices de la hipérbola.
En este caso, al estar los focos sobre el eje x, los vértices reales se ubican en A1(-a;0) y A2(a;0), mientras que los vértices imaginarios se encuentran en B1(0;-b) y B2(0;b).
Con a=3 y b=4, obtenemos: A1(-3;0), A2(3;0), B1(0;-4) y B2(0;4).
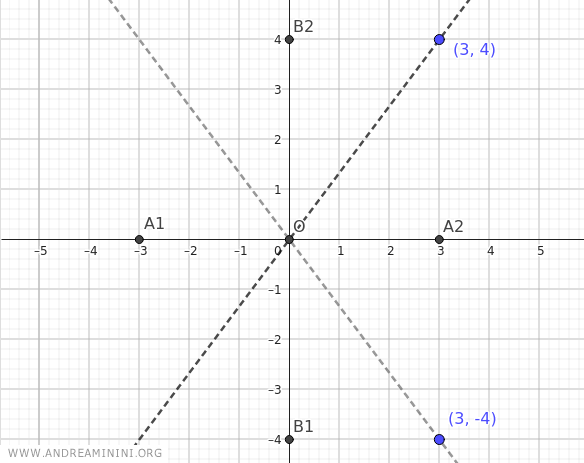
A continuación, calculamos las coordenadas (x;y) de los focos de la hipérbola.
Los focos se sitúan a una distancia "c" del centro, y esta se obtiene mediante la fórmula:
$$ c = \sqrt{a^2+b^2} $$
Sustituyendo los valores:
$$ c = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5 $$
Como el eje principal es el eje x, los focos están en F1(-5;0) y F2(5;0).
Ahora buscamos otros puntos de la hipérbola a partir de su ecuación canónica:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$
En este caso, el término constante es +1, ya que los focos están sobre el eje x.
Despejamos y en función de x:
$$ - \frac{y^2}{b^2} = 1 - \frac{x^2}{a^2} $$
$$ - y^2 = b^2 \cdot \left(1 - \frac{x^2}{a^2}\right) $$
Multiplicamos por -1:
$$ y^2 = b^2 \cdot \left(\frac{x^2}{a^2} - 1\right) $$
Extraemos la raíz cuadrada:
$$ y = \pm \sqrt{b^2 \cdot \left(\frac{x^2}{a^2} - 1\right)} $$
Reemplazamos a=3 y b=4:
$$ y = \pm \sqrt{16 \cdot \left(\frac{x^2}{9} - 1\right)} $$
Así obtenemos el valor de y para cualquier x perteneciente al dominio de la hipérbola: (-∞,-3]∪[3,∞).
| x | y |
|---|---|
| -5 | ±5.33 |
| -4 | ±3.53 |
| -3 | 0 |
| 3 | 0 |
| 4 | ±3.53 |
| 5 | ±5.33 |
Con estos puntos ya es posible esbozar la forma general de la hipérbola.
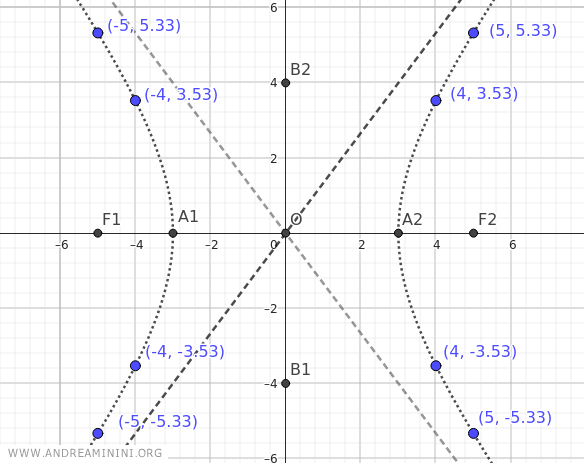
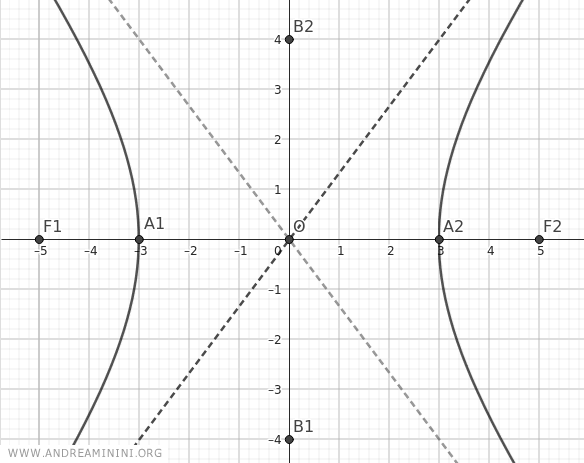
Para una representación más precisa, se pueden calcular más coordenadas.
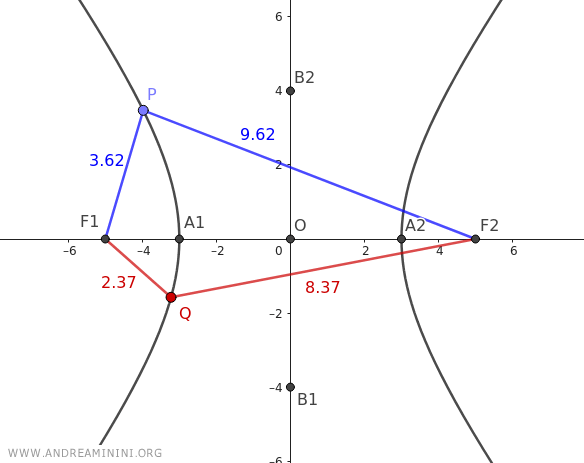
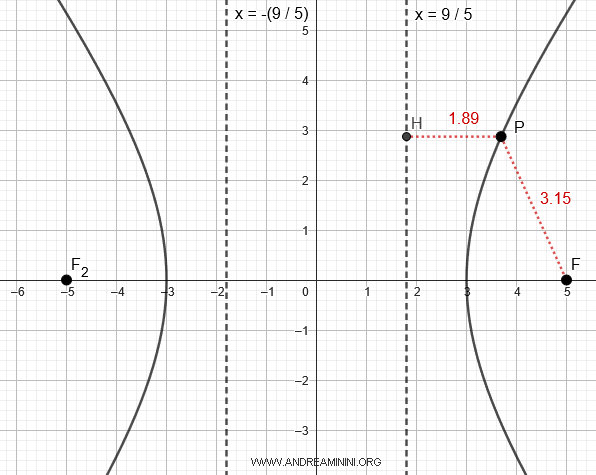
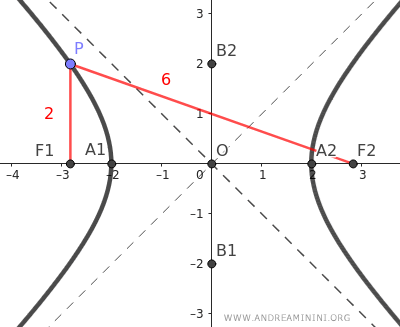
Nota: Como se explicó antes, una hipérbola es el lugar geométrico donde cada punto mantiene constante la diferencia absoluta de distancias a los focos. Podemos comprobarlo con dos puntos P y Q sobre la curva. El punto P (azul) está a 3.62 de F1 y a 9.62 de F2, por lo que la diferencia es |9.62 - 3.62| = 6. El punto Q (rojo) está a 2.37 de F1 y a 8.37 de F2, así que también se cumple |8.37 - 2.37| = 6. Esta propiedad se verifica en cualquier punto de la hipérbola.
En este ejemplo, el eje transverso coincide con el eje x, por lo que las rectas directrices vienen dadas por:
$$ x = \pm \frac{a^2}{c} = \pm \frac{9}{5} $$
La razón entre la distancia $ \overline{PF} $ desde un punto $ P(x;y) $ al foco $ F(c,0) $ y la distancia $ \overline{PH} $ desde ese mismo punto a la directriz es constante y corresponde a la excentricidad (e) de la hipérbola.
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
Por ejemplo, para el punto $ P $, se tiene $ \overline{PF} = 3.15 $ y $ \overline{PH} = 1.89 $.
$$ e = \frac{3.15}{1.89} = 1.67 $$
Este valor $ e = 1.67 $ se mantiene constante para cualquier otro punto de la curva.
Nota: Otra forma de obtener la excentricidad de una hipérbola es mediante la fórmula $$ e = \frac{c}{a} $$. En este caso, con $ c = 5 $ y $ a = 3 $, se obtiene: $$ e = \frac{5}{3} = 1.67 $$. El resultado es el mismo.
Ejemplo 2
En este ejemplo, analizamos una hipérbola cuyos focos se encuentran sobre el eje y y cuyo centro está en el origen del sistema cartesiano, O(0;0), utilizando los mismos valores de a = 3 y b = 4 que en el ejemplo anterior.
Las asíntotas son las rectas que pasan por el origen y por los puntos (a;b) y (a;-b), es decir, (3;4) y (3;-4).
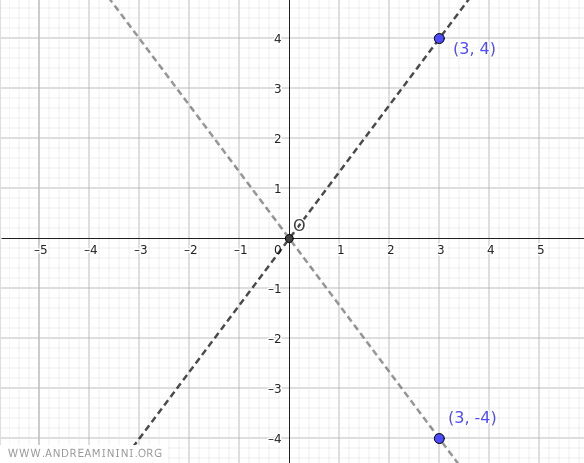
Como puede observarse, las asíntotas son idénticas a las del caso anterior.
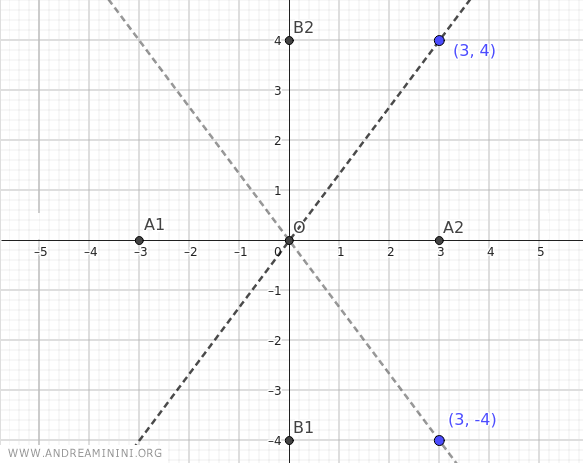
Los vértices de la hipérbola también se mantienen, aunque en este caso los vértices reales son B1(0;-b) y B2(0;b), mientras que los vértices imaginarios corresponden a A1(-a;0) y A2(a;0).
En otras palabras, en esta configuración, la curva de la hipérbola pasa por los puntos B1 y B2.
Dado que a = 3 y b = 4, los vértices reales se ubican en B1(0;-4) y B2(0;4), mientras que los imaginarios están en A1(-3;0) y A2(3;0).
Los focos de la hipérbola siempre se encuentran a una distancia “c” del centro de la curva.
La fórmula para calcular dicha distancia es:
$$ c = \sqrt{a^2 + b^2} $$
Sustituyendo a = 3 y b = 4:
$$ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 $$
En este caso, el eje principal es el eje y.
Por lo tanto, las coordenadas de los focos son distintas a las del ejemplo anterior. Se encuentran en F1(0;-c) y F2(0;c), con c = 5:
$$ F_1(0;-5) $$
$$ F_2(0;5) $$
Colocamos los focos F1(0;-5) y F2(0;5) en el plano cartesiano.
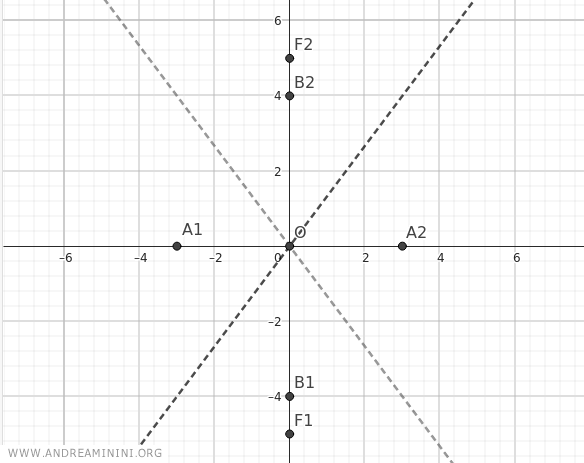
Ahora calculamos distintos puntos de la curva utilizando la ecuación canónica de la hipérbola:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
En este caso, el término constante es -1 porque los focos se encuentran sobre el eje y.
Despejamos y en función de x:
$$ y = \sqrt{b^2 \cdot \left( \frac{x^2}{a^2} + 1 \right)} $$
Sustituyendo a = 3 y b = 4:
$$ y = \sqrt{4^2 \cdot \left( \frac{x^2}{3^2} + 1 \right)} $$
$$ y = \sqrt{16 \cdot \left( \frac{x^2}{9} + 1 \right)} $$
Con esta expresión, podemos obtener las coordenadas (x;y) para distintos valores de x dentro del dominio real: (-∞, +∞).
| x | y |
|---|---|
| -2 | ±4.81 |
| -1 | ±4.22 |
| 0 | 0 |
| 1 | ±4.22 |
| 2 | ±4.81 |
| 3 | ±5.66 |
Estos primeros puntos permiten trazar con bastante precisión la forma de la hipérbola.
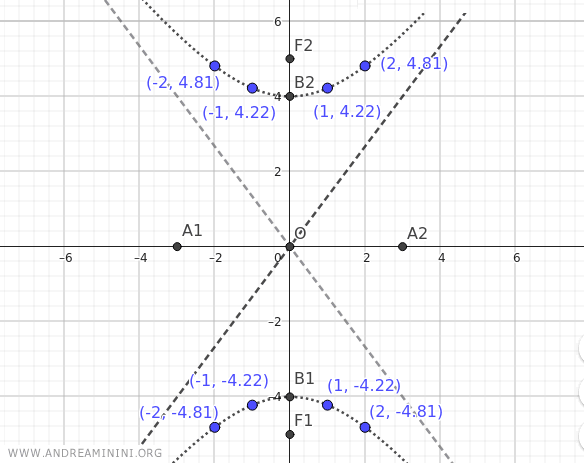
El resultado final es una hipérbola cuyos focos se encuentran sobre el eje y.
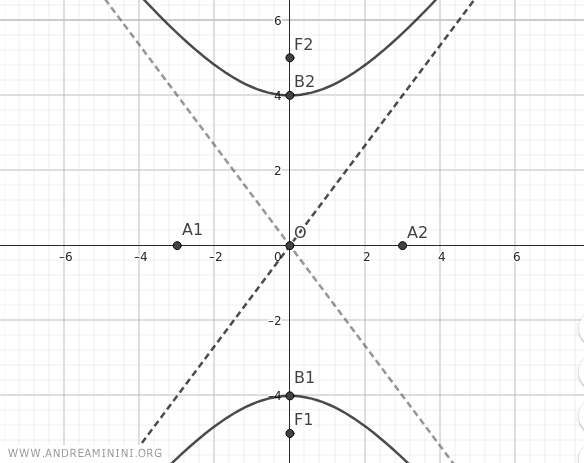
En este caso, el eje transverso - que contiene los focos - coincide con el eje y.
Por consiguiente, las rectas directrices son perpendiculares al eje y:
$$ y = \pm \frac{b^2}{c} = \frac{16}{5} = 3.2 $$
También aquí, la razón entre las distancias $ \overline{PF} $ (del punto al foco) y $ \overline{PH} $ (del punto a la directriz) permanece constante y coincide con la excentricidad e de la hipérbola:
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
Por ejemplo, para un punto $ P $, se tiene $ \overline{PF} = 3.69 $ y $ \overline{PH} = 2.95 $.
$$ e = \frac{3.69}{2.95} = 1.25 $$
Este valor de excentricidad, $ e = 1.25 $, se mantiene constante para cualquier otro punto de la curva.
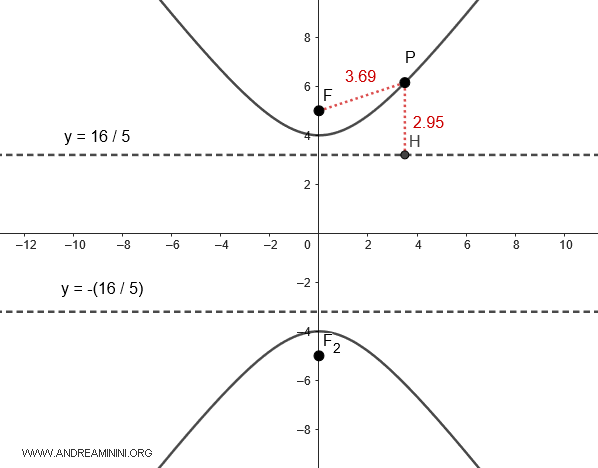
Nota: Otra forma de calcular la excentricidad de una hipérbola con eje focal sobre el eje y es mediante la fórmula $$ e = \frac{c}{b} = \frac{5}{4} = 1.25 $$. El resultado obtenido es, naturalmente, el mismo.
Notas
Algunas observaciones y comentarios adicionales sobre la hipérbola:
- Hipérbola equilátera
La hipérbola equilátera es un caso particular en el que se cumple que a = b. En este tipo de hipérbola, tanto los vértices reales sobre el eje transverso (A1, A2) como los vértices imaginarios sobre el eje conjugado (B1, B2) se encuentran a igual distancia del centro.
- Una recta puede intersectar una hipérbola en, como máximo, dos puntos reales
- Si una recta corta la hipérbola en dos puntos distintos, se denomina secante.
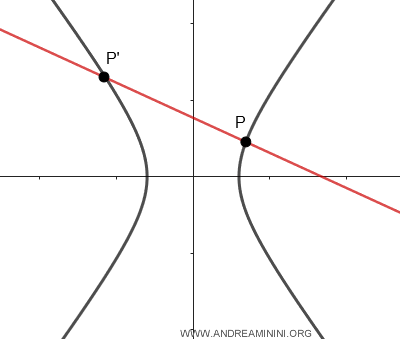
- Si la recta toca la hipérbola en un único punto, se llama tangente.
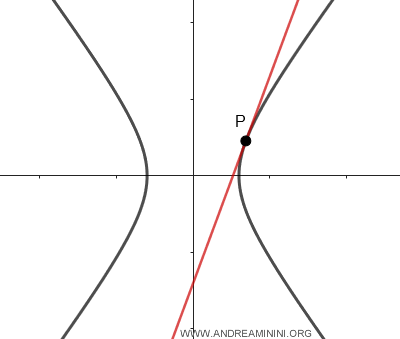
Nota: Desde cualquier punto exterior P' del plano pueden trazarse, como máximo, dos tangentes a la hipérbola. En cambio, si el punto P pertenece a la curva, existe una única tangente definida en ese punto.
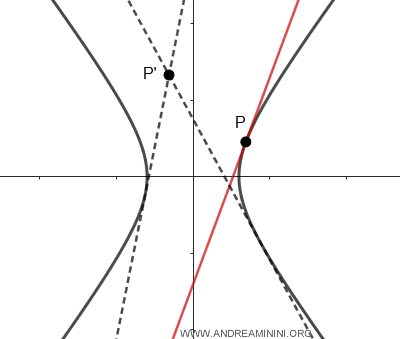
- Si una recta no corta la hipérbola en ningún punto, se denomina exterior.
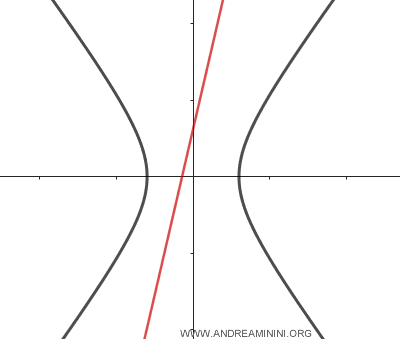
- Si una recta corta la hipérbola en dos puntos distintos, se denomina secante.
- Propiedad focal de la hipérbola
En una hipérbola, si se traza una tangente \( t \) en un punto \( P \) de la curva, la perpendicular \( n \) a dicha tangente en \( P \) biseca el ángulo formado entre el radio focal \( PF_1 \) y la prolongación del otro radio focal \( PF_2 \), generando dos ángulos iguales \( \alpha \cong \beta \).
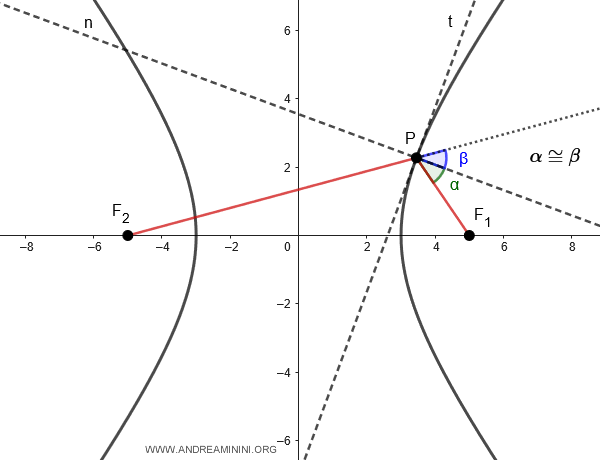
Esta propiedad implica que, si un foco (por ejemplo, F1) actúa como fuente de un rayo de luz, dicho rayo se reflejará en la curva como si procediera del otro foco (F2), siguiendo el mismo principio óptico de un espejo hiperbólico.
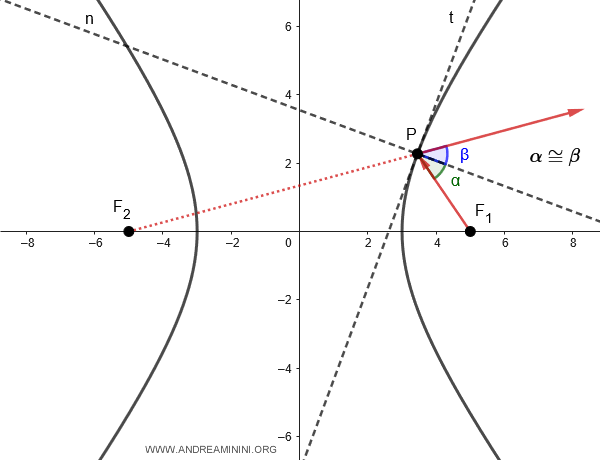
Y así sucesivamente.