Cómo hallar la ecuación de una hipérbola a partir de un punto y un foco

Para determinar la ecuación de una hipérbola con centro en el origen, dados un punto \( P(x_0, y_0) \) y uno de sus focos \( F(c, 0) \), se pueden seguir dos enfoques distintos:

• Plantear un sistema de ecuaciones utilizando la identidad \( c^2 = a^2 + b^2 \) junto con la ecuación de la hipérbola, sustituyendo \( x \) e \( y \) por las coordenadas del punto \( P(x_0, y_0) \): $$ \begin{cases} \frac{x_0^2}{a^2} - \frac{y_0^2}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$
• Calcular la distancia entre el punto \( P \) y los focos, sabiendo que \( | PF - PF' | = 2a \). Una vez conocido el valor de \( a \), que representa la semidistancia entre los vértices, se puede hallar \( b \) utilizando la relación \( c^2 = a^2 + b^2 \).

Nota: Si el foco se encuentra sobre el eje x, la ecuación de la hipérbola es $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$. En cambio, si el foco está sobre el eje y, la ecuación correspondiente es $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$.

Método 1

Supongamos que tenemos una hipérbola con centro en el origen que pasa por el punto \( P(3, 4) \) y cuyo foco se encuentra en \( F(5, 0) \).

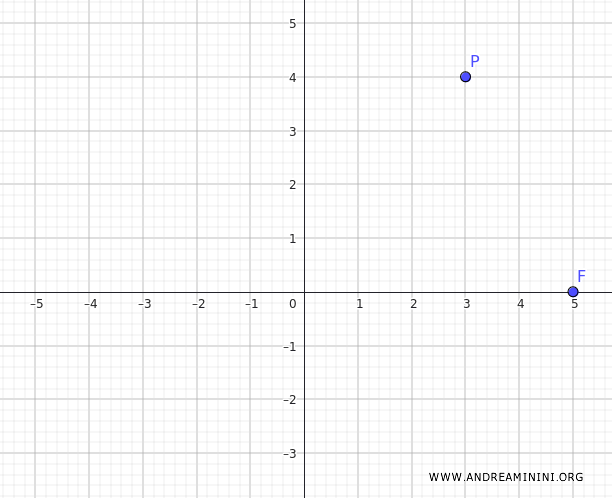
Como el foco está sobre el eje x, usamos la forma canónica de la ecuación de una hipérbola horizontal:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Planteamos un sistema usando esta ecuación y la relación entre los parámetros:

$$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$

Sustituimos \( x = 3 \) y \( y = 4 \), es decir, las coordenadas del punto \( P \):

$$ \begin{cases} \frac{3^2}{a^2} - \frac{4^2}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$

$$ \begin{cases} \frac{9}{a^2} - \frac{16}{b^2} = 1 \\ \\ c^2 = a^2 + b^2 \end{cases} $$

Dado que el foco es \( F(c, 0) = (5, 0) \), sabemos que \( c = 5 \):

$$ \begin{cases} \frac{9}{a^2} - \frac{16}{b^2} = 1 \\ \\ 25 = a^2 + b^2 \end{cases} $$

Resolvemos el sistema por sustitución:

$$ \begin{cases} \frac{9}{25 - b^2} - \frac{16}{b^2} = 1 \\ \\ a^2 = 25 - b^2 \end{cases} $$

Multiplicamos ambos lados por \( b^2(25 - b^2) \):

$$ \begin{cases} 9b^2 - 16(25 - b^2) = b^2(25 - b^2) \\ \\ a^2 = 25 - b^2 \end{cases} $$

Desarrollamos los términos:

$$ \begin{cases} 9b^2 - 400 + 16b^2 = 25b^2 - b^4 \\ \\ a^2 = 25 - b^2 \end{cases} $$

Reordenamos los términos:

$$ \begin{cases} b^4 - 400 = 0 \\ \\ a^2 = 25 - b^2 \end{cases} $$

Calculamos la raíz cuadrada:

$$ \begin{cases} b^2 = 20 \\ \\ a^2 = 5 \end{cases} $$

Nota: Aunque \( \sqrt{400} = \pm 20 \), descartamos el valor negativo, ya que \( b \) representa una longitud.

Con \( a^2 = 5 \) y \( b^2 = 20 \), podemos escribir la ecuación de la hipérbola:

$$ \frac{x^2}{5} - \frac{y^2}{20} = 1 $$

Ésta es la ecuación de la hipérbola que pasa por \( P(3,4) \) y tiene su foco en \( F(5,0) \).

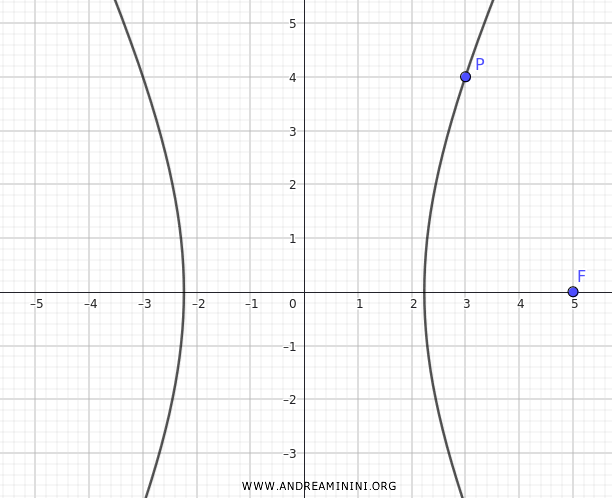
Método 2

Consideramos nuevamente la hipérbola con centro en el origen, que pasa por el punto \( P(3, 4) \) y tiene como foco a \( F(5, 0) \).

Sabemos que \( c = 5 \), ya que el foco está a 5 unidades del centro.

Usamos la misma forma canónica de la ecuación:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Calculamos la distancia entre el punto \( P \) y el foco \( F \):

$$ \overline{PF} = \sqrt{(3 - 5)^2 + 4^2} = \sqrt{4 + 16} = \sqrt{20} = 2\sqrt{5} $$

El otro foco es \( F'(-5, 0) \). Calculamos ahora \( PF' \):

$$ PF' = \sqrt{(3 + 5)^2 + 4^2} = \sqrt{64 + 16} = \sqrt{80} = 4\sqrt{5} $$

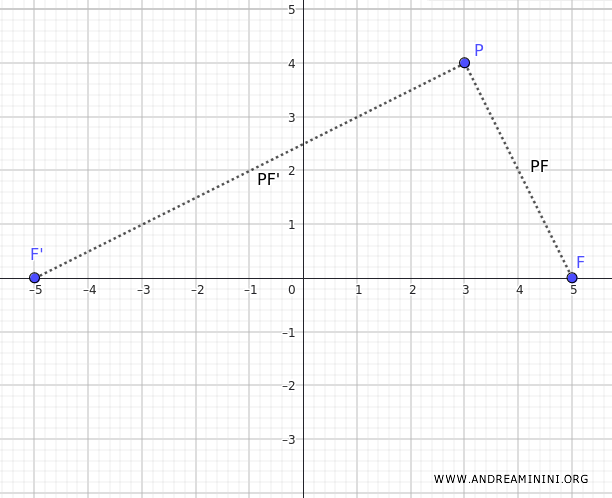
La definición de hipérbola implica que la diferencia de distancias a los focos es constante e igual a \( 2a \):

$$ |PF - PF'| = 2a $$

Por tanto:

$$ |2\sqrt{5} - 4\sqrt{5}| = 2a $$

$$ 2\sqrt{5} = 2a \Rightarrow a = \sqrt{5} $$

Usamos la relación \( c^2 = a^2 + b^2 \) con \( c = 5 \) y \( a = \sqrt{5} \):

$$ 25 = 5 + b^2 \Rightarrow b^2 = 20 $$

Finalmente, sustituimos \( a^2 = 5 \) y \( b^2 = 20 \) en la ecuación estándar:

$$ \frac{x^2}{5} - \frac{y^2}{20} = 1 $$

Ésta es la ecuación de la hipérbola que pasa por el punto \( (3, 4) \) y tiene uno de sus focos en \( (5, 0) \).