Ecuación de una hipérbola a partir de la excentricidad y un vértice
Para deducir la ecuación de una hipérbola con centro en el origen, conociendo su excentricidad y uno de sus vértices $ A(a;0) $ o $ B(0;b) $, sigue los pasos que se indican a continuación:
- Si los focos se encuentran sobre el eje x, la ecuación de la hipérbola es $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ y la excentricidad se expresa como $$ e = \frac{c}{a} $$
- Si los focos están sobre el eje y, la ecuación correspondiente es $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$ y la excentricidad viene dada por $$ e = \frac{c}{b} $$
En ambos casos, la relación entre los semiejes $ a $, $ b $ y la distancia del centro a cada foco $ c $ está dada por la fórmula:
$$ c^2 = a^2 + b^2 $$
Nota: Si el enunciado no indica claramente sobre qué eje se sitúan los focos, conviene analizar ambos casos: que el eje transversal sea el eje x o el eje y.
Un ejemplo práctico
Supongamos que tenemos una hipérbola centrada en el origen, con un vértice no real en $ A(-2;0) $ y una excentricidad igual a $ e = \frac{3 \sqrt{5}}{5} $.
Como el vértice $ A(-2;0) $ está sobre el eje x, y el enunciado indica que se trata de un vértice "no real", se deduce que el eje real (es decir, el que contiene los focos) es el eje y.
Cuando el eje real o transversal es el eje y, la ecuación de la hipérbola toma la forma:
$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$
Y la excentricidad se define como:
$$ e = \frac{c}{b} $$
Planteamos entonces el siguiente sistema:
$$ \begin{cases} e = \frac{c}{b} \\ \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 \end{cases} $$
Con $ e = \frac{3 \sqrt{5}}{5} $ y el vértice $ A(a;0) = (2;0) $, es decir, $ a = 2 $, tenemos:
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{c}{b} \\ \\ \frac{x^2}{2^2} - \frac{y^2}{b^2} = 1 \end{cases} $$
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{c}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
Sabemos que $ c^2 = a^2 + b^2 $, por lo que podemos escribir $ c = \sqrt{a^2 + b^2} $ con $ a = 2 $:
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{\sqrt{a^2 + b^2}}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{\sqrt{2^2 + b^2}}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{3 \sqrt{5}}{5} = \frac{\sqrt{4 + b^2}}{b} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
Elevamos al cuadrado ambos miembros de la primera ecuación:
$$ \begin{cases} \left( \frac{3 \sqrt{5}}{5} \right)^2 = \left( \frac{\sqrt{4 + b^2}}{b} \right)^2 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9 \cdot 5}{25} = \frac{4 + b^2}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9}{5} = \frac{4}{b^2} + \frac{b^2}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9}{5} = \frac{4}{b^2} + 1 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{9}{5} - 1 = \frac{4}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \frac{4}{5} = \frac{4}{b^2} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} b^2 = \frac{5}{4} \cdot 4 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} b^2 = 5 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} \sqrt{b^2} = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
$$ \begin{cases} b = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = -1 \end{cases} $$
Ya que $ b = \sqrt{5} $, sustituimos este valor en la segunda ecuación:
$$ \begin{cases} b = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{(\sqrt{5})^2} = -1 \end{cases} $$
$$ \begin{cases} b = \sqrt{5} \\ \\ \frac{x^2}{4} - \frac{y^2}{5} = -1 \end{cases} $$
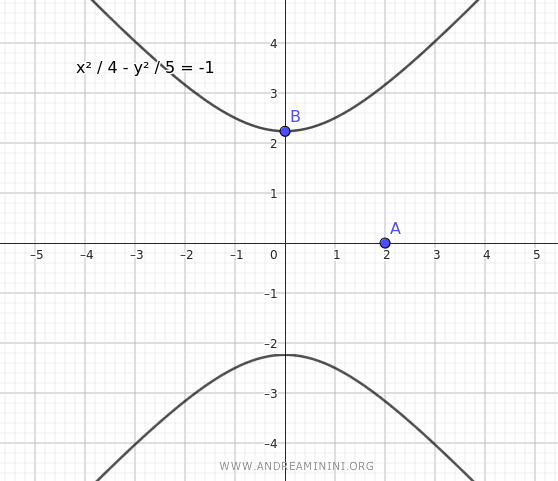
Por tanto, la ecuación de la hipérbola centrada en el origen, con vértice no real en $ A(-2;0) $ y excentricidad $ e = \frac{3 \sqrt{5}}{5} $, es:
$$ \frac{x^2}{4} - \frac{y^2}{5} = -1 $$
A continuación, se muestra su representación gráfica:
Y así continúa.