Cómo determinar la ecuación de una hipérbola a partir de un foco y una recta tangente

Si se conoce uno de los focos de una hipérbola y una recta tangente, es posible obtener su ecuación siguiendo estos pasos:

• En primer lugar, identifica si el eje transverso está alineado con el eje x $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ o con el eje y $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$. Esto permite establecer la forma canónica de la hipérbola.
• Utiliza las coordenadas del foco para aplicar la relación \( c^2 = a^2 + b^2 \), donde \(a\) y \(b\) son los semiejes.
• Luego, compara la ecuación de la recta tangente con la forma general de la tangente a una hipérbola: \( \frac{x_0x}{a^2} - \frac{y_0y}{b^2} = 1 \). A partir de ella, deduce las coordenadas \( (x_0, y_0) \) del punto de tangencia en función de \( a^2 \) y \( b^2 \), y sustitúyelas en la ecuación de la recta para obtener una segunda relación entre las variables.
• Por último, resuelve el sistema formado por las dos ecuaciones para encontrar los valores de \( a^2 \) y \( b^2 \).

Siguiendo este procedimiento, se puede deducir la ecuación de la hipérbola.

Ejemplo

Sea una hipérbola con centro en el origen, cuyo foco se encuentra en \( F( \sqrt{7}, 0 ) \), y que tiene por tangente la recta \( x - y = 1 \).

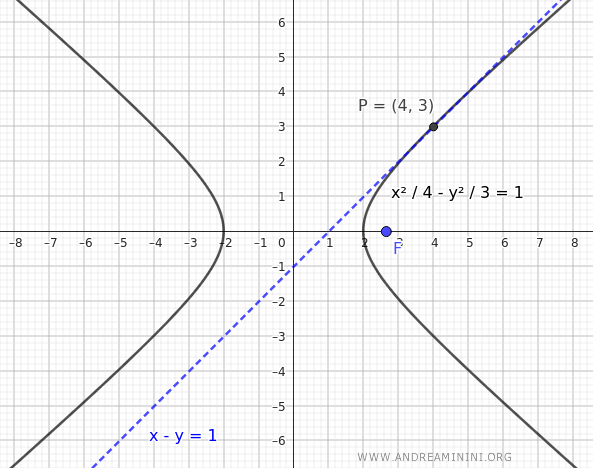
Dado que el foco está sobre el eje x, la ecuación de la hipérbola es:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Aquí, \(a\) y \(b\) representan las longitudes de los semiejes. Como los focos se sitúan sobre el eje x, se utiliza la relación \( c^2 = a^2 + b^2 \), donde \(c\) es la distancia del centro al foco.

Como el foco está en \( F( \sqrt{7}, 0 ) \), se tiene:

$$ c = \sqrt{7} $$

Aplicando la fórmula:

$$ c^2 = a^2 + b^2 $$

$$ (\sqrt{7})^2 = a^2 + b^2 $$

$$ a^2 + b^2 = 7 \quad \text{(Ecuación 1)} $$

Necesitamos ahora una segunda ecuación que relacione \(a\) y \(b\).

La recta tangente dada es \(x - y = 1\).

Recordemos que la ecuación general de la tangente a una hipérbola en el punto \( (x_0, y_0) \) es:

$$ \frac{x_0x}{a^2} - \frac{y_0y}{b^2} = 1 $$

Comparando con la recta \(x - y = 1\), obtenemos:

$$ \underbrace{ \frac{x_0}{a^2} }_1 x - \underbrace{ \frac{y_0}{b^2} }_1 y = 1 \Leftrightarrow x - y = 1 $$

De esta correspondencia se deduce que:

$$ \frac{x_0}{a^2} = 1 \quad \text{y} \quad -\frac{y_0}{b^2} = -1 $$

Es decir:

$$ x_0 = a^2 \quad \text{y} \quad y_0 = b^2 $$

Por tanto, el punto de tangencia sobre la hipérbola es \( (a^2, b^2) \).

Este punto también pertenece a la recta tangente, por lo que al sustituir \(x = a^2\) y \(y = b^2\) en la ecuación \(x - y = 1\) se obtiene:

$$ a^2 - b^2 = 1 \quad \text{(Ecuación 2)} $$

Ya tenemos un sistema de dos ecuaciones con dos incógnitas:

$$ \begin{cases} a^2 + b^2 = 7 \\ \\ a^2 - b^2 = 1 \end{cases} $$

Despejamos \(a^2\) en la primera ecuación:

$$ a^2 = 7 - b^2 $$

Y sustituimos en la segunda:

$$ 7 - b^2 - b^2 = 1 $$

$$ -2b^2 = -6 $$

$$ b^2 = 3 $$

Una vez conocido \(b^2\), sustituimos en la primera ecuación para hallar \(a^2\):

$$ a^2 = 7 - 3 = 4 $$

Con estos valores, podemos escribir la ecuación de la hipérbola:

$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$

Esta es la ecuación de la hipérbola con foco en \( F( \sqrt{7}, 0 ) \) y tangente \( x - y = 1 \).

Así se llega, paso a paso, a la ecuación buscada.