Recta secante, tangente o exterior a una hipérbola
Una recta de la forma $$ a'x + b'y + c = 0 $$ y una hipérbola $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 $$ pueden intersectarse de tres maneras distintas: como secante, tangente o exterior.
- Si se cortan en dos puntos distintos, la recta es secante.
- Si se intersectan en un solo punto, puede tratarse de una tangente o de una recta paralela a una asíntota.
- Si no tienen ningún punto en común, la recta es exterior.
Por tanto, el hecho de que haya un único punto de intersección no garantiza necesariamente que la recta sea tangente.
Para determinar la posición relativa de la recta respecto a la hipérbola, debemos resolver el siguiente sistema de ecuaciones:
$$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \\ \\ a'x + b'y + c = 0 \end{cases} $$
A continuación, se analiza la ecuación resolvente.
- Si la ecuación resolvente es de segundo grado:
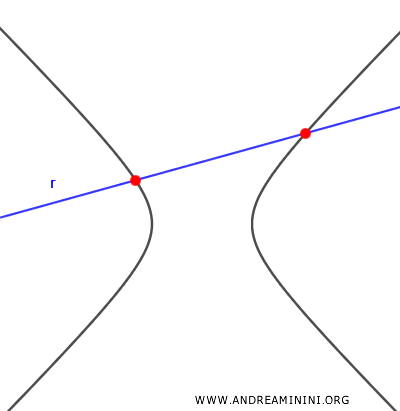
- $ \Delta > 0 $
Si el discriminante es positivo, existen dos soluciones reales y la recta corta a la hipérbola en dos puntos distintos.
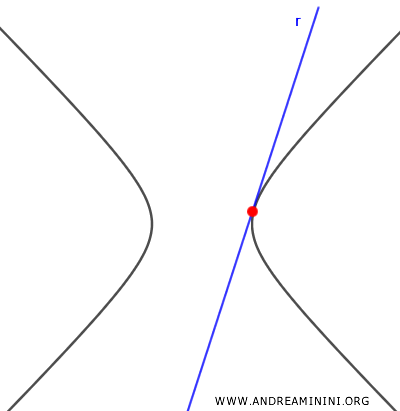
- $ \Delta = 0 $
Si el discriminante es nulo, hay una única solución real y la recta es tangente a la hipérbola.
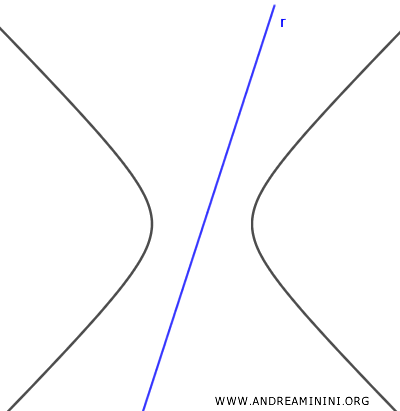
- $ \Delta < 0 $
Si el discriminante es negativo, no hay soluciones reales y la recta es exterior a la hipérbola.
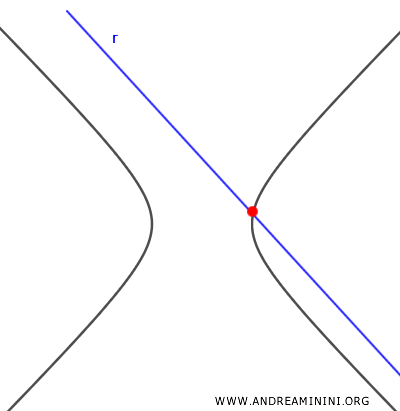
- $ \Delta > 0 $
- Si la ecuación resolvente es de primer grado, la recta intersecta a la hipérbola en un único punto.
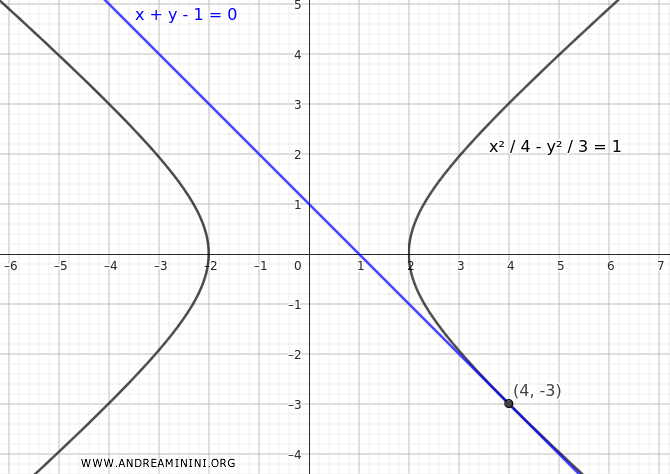
Ejemplo práctico
Consideremos la hipérbola:
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
y la recta:
$$ x + y - 1 = 0 $$
Queremos determinar si la recta es tangente, secante o exterior.
Planteamos el sistema:
$$ \begin{cases} \frac{x^2}{4} - \frac{y^2}{3} = 1 \\ \\ x + y - 1 = 0 \end{cases} $$
Despejamos \( y \) en ambas ecuaciones:
$$ \begin{cases} y^2 = 3 \cdot \left( \frac{x^2}{4} - 1 \right) \\ \\ y = 1 - x \end{cases} $$
$$ \begin{cases} y = \sqrt{ \frac{3x^2}{4} - 3 } \\ \\ y = 1 - x \end{cases} $$
Igualamos ambas expresiones de \( y \) para obtener la ecuación resolvente:
$$ \sqrt{ \frac{3x^2}{4} - 3 } = 1 - x $$
$$ \left( \sqrt{ \frac{3x^2}{4} - 3 } \right)^2 = (1 - x)^2 $$
$$ \frac{3x^2}{4} - 3 = 1 - 2x + x^2 $$
$$ \frac{3x^2}{4} - 4 + 2x - x^2 = 0 $$
$$ \frac{3x^2 - 4x^2}{4} + 2x - 4 = 0 $$
$$ -\frac{x^2}{4} + 2x - 4 = 0 $$
La ecuación resolvente es de segundo grado, por lo que la recta no es paralela a una asíntota de la hipérbola.
Calculamos el discriminante:
$$ \Delta = b^2 - 4ac $$
Donde $ a = - \frac{1}{4} $, $ b = 2 $, $ c = -4 $
$$ \Delta = 2^2 - 4 \cdot (- \frac{1}{4}) \cdot (-4) $$
$$ \Delta = 4 - 4 $$
$$ \Delta = 0 $$
Como el discriminante es cero, la recta es tangente a la hipérbola.
Calculamos la coordenada \( x \) del punto de tangencia:
$$ x = \frac{-b \pm \Delta}{2a} $$
$$ x = \frac{-2 \pm 0}{2 \cdot (- \frac{1}{4})} = \frac{-2}{- \frac{1}{2}} = 4 $$
Con \( x = 4 \), sustituimos en la ecuación de la recta para hallar \( y \):
$$ y = 1 - x = 1 - 4 = -3 $$
Por tanto, el punto de tangencia es $ (x; y) = (4; -3) $
Ejemplo 2
Consideremos nuevamente la hipérbola:
$$ \frac{x^2}{4} - \frac{y^2}{3} = 1 $$
y la recta:
$$ y = - \frac{ \sqrt{3} }{2} x + \frac{1}{2} $$
Queremos averiguar si esta recta es secante, tangente o exterior.
Nota: Al observar la pendiente de la recta, $ -\frac{ \sqrt{3} }{2} $, ya podemos advertir que es paralela a una de las asíntotas de la hipérbola. Recordemos que las asíntotas están dadas por $$ y = \pm \frac{b}{a}x $$ En este caso, como $ a^2 = 4 $ y $ b^2 = 3 $, tenemos $ a = 2 $ y $ b = \sqrt{3} $, lo que nos da $$ y = \pm \frac{\sqrt{3}}{2}x $$ Así que efectivamente, la pendiente coincide con la de una asíntota. Esto nos sugiere que la recta intercepta la hipérbola en un único punto. No obstante, confirmaremos este resultado con los cálculos.
Planteamos el sistema:
$$ \begin{cases} \frac{x^2}{4} - \frac{y^2}{3} = 1 \\ \\ y = - \frac{ \sqrt{3} }{2} x + \frac{1}{2} \end{cases} $$
$$ \begin{cases} y^2 = 3 \cdot \left( \frac{x^2}{4} - 1 \right) \\ \\ y = - \frac{ \sqrt{3} }{2} x + \frac{1}{2} \end{cases} $$
$$ \begin{cases} y = \sqrt{ \frac{3x^2}{4} - 3 } \\ \\ y = - \frac{ \sqrt{3} }{2} x + \frac{1}{2} \end{cases} $$
Igualamos ambas expresiones de \( y \):
$$ \sqrt{ \frac{3x^2}{4} - 3 } = - \frac{ \sqrt{3} }{2} x + \frac{1}{2} $$
$$ \left( \sqrt{ \frac{3x^2}{4} - 3 } \right)^2 = \left( - \frac{ \sqrt{3} }{2} x + \frac{1}{2} \right)^2 $$
$$ \frac{3x^2}{4} - 3 = \frac{3}{4} x^2 - \frac{ \sqrt{3} x }{2} + \frac{1}{4} $$
$$ \require{cancel} \cancel{ \frac{3x^2}{4} } - 3 - \cancel{ \frac{3}{4} x^2 } + \frac{ \sqrt{3} x }{2} - \frac{1}{4} = 0 $$
$$ \frac{ \sqrt{3} x }{2} - 3 - \frac{1}{4} = 0 $$
$$ \frac{ \sqrt{3} x }{2} - \frac{12}{4} - \frac{1}{4} = 0 $$
$$ \frac{ \sqrt{3} x }{2} - \frac{13}{4} = 0 $$
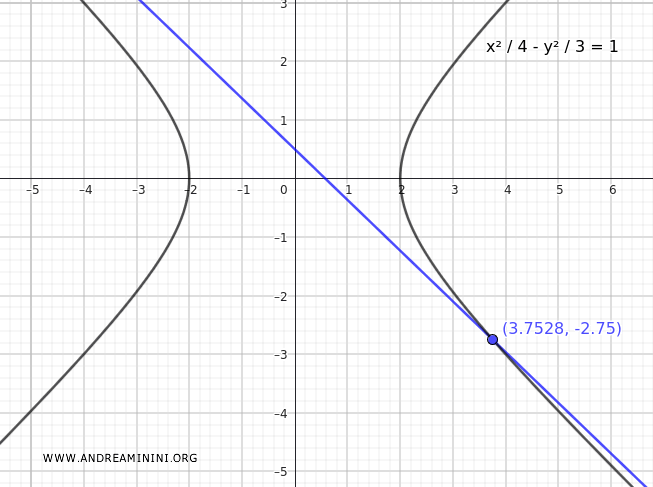
La ecuación resolvente es de primer grado, lo que confirma que la recta corta a la hipérbola en un solo punto.
Esto significa que la recta es paralela a una de las asíntotas.
Calculamos la coordenada \( x \) del punto de intersección:
$$ x = \frac{13}{4} \cdot \frac{2}{\sqrt{3}} = \frac{13}{2\sqrt{3}} $$
Nota: Las asíntotas de la hipérbola son $$ y = \pm \frac{b}{a}x $$ con $ a = 2 $ y $ b = \sqrt{3} $, por tanto $$ y = \pm \frac{\sqrt{3}}{2}x $$ La pendiente de la recta $ -\frac{ \sqrt{3} }{2} $ coincide exactamente con la de una asíntota.
Calculamos la coordenada \( y \):
$$ y = - \frac{ \sqrt{3} }{2} \cdot \frac{13}{2 \sqrt{3}} + \frac{1}{2} $$
$$ y = - \frac{13}{4} + \frac{1}{2} = \frac{-13 + 2}{4} = -\frac{11}{4} $$
El gráfico muestra la hipérbola y la recta intersectándose en un único punto:
Y así sucesivamente.