Determinación de la ecuación de una hipérbola a partir de un vértice y una recta tangente

Para obtener la ecuación de una hipérbola con centro en el origen, conociendo una recta tangente y uno de sus vértices, se procede de la siguiente manera:

• En primer lugar, se identifica el eje transverso (el eje sobre el que se encuentran los focos) a partir de los datos disponibles. Si el eje transverso es el eje x, la ecuación de la hipérbola es: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1   $$ En cambio, si el eje transverso es el eje y, la ecuación será: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1   $$
• Se plantea un sistema de ecuaciones que combina la forma canónica de la hipérbola con la ecuación de la recta tangente: $$ \begin{cases} \frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \\ \\ a'x + b'y + c' = 0 \end{cases} $$
• Se sustituyen las coordenadas del vértice conocido y se resuelve el sistema para determinar el valor del semieje desconocido, teniendo en cuenta que la condición de tangencia se cumple cuando el discriminante de la ecuación resultante es cero: $ \Delta = 0 $

Ejemplo práctico

Consideremos una hipérbola con centro en el origen, tangente a la recta $ 2x - 3y - 2 = 0 $ y con vértice real en $ A(2;0) $.

Como el vértice real se encuentra en $ A(2;0) $, se deduce que $ a = 2 $ y que el eje transverso coincide con el eje x. Por tanto, la ecuación de la hipérbola es:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{2^2} - \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{4} - \frac{y^2}{b^2} = 1 $$

Planteamos ahora un sistema formado por esta ecuación y la de la recta tangente:

$$ \begin{cases} 2x - 3y - 2 = 0 \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = 1 \end{cases} $$

Para comprobar que la recta es tangente, sustituimos su expresión en la ecuación de la hipérbola y verificamos que se obtiene una única solución. Esto garantiza que la recta toca la hipérbola en un solo punto.

$$ \begin{cases} y = \frac{2x - 2}{3} \\ \\ \frac{x^2}{4} - \frac{y^2}{b^2} = 1 \end{cases} $$

Sustituimos \( y \) en la ecuación de la hipérbola:

$$ \begin{cases} y = \frac{2x - 2}{3} \\ \\ \frac{x^2}{4} - \frac{\left( \frac{2x - 2}{3}  \right)^2}{b^2} = 1 \end{cases} $$

$$ \begin{cases} y = \frac{2x - 2}{3} \\ \\ \frac{x^2}{4} - \frac{ \frac{4x^2 - 8x + 4 }{9}  }{b^2} = 1 \end{cases} $$

$$ \begin{cases} y = \frac{2x - 2}{3} \\ \\ \frac{x^2}{4} - \frac{4x^2 - 8x + 4}{9b^2} = 1 \end{cases} $$

Multiplicamos ambos miembros por $ 36b^2 $ para eliminar denominadores:

$$ 9b^2x^2 - 16x^2 + 32x - 16 = 36b^2 $$

Reordenamos los términos:

$$ (9b^2 - 16)x^2 + 32x - 16 - 36b^2 = 0 $$

Para que exista tangencia, esta ecuación cuadrática debe tener una única raíz real, es decir, su discriminante debe ser nulo.

Recordemos que el discriminante de una ecuación cuadrática \( Ax^2 + Bx + C = 0 \) es \( \Delta = B^2 - 4AC \).

En este caso: $ A = 9b^2 - 16,\quad B = 32,\quad C = -16 - 36b^2 $.

Entonces:

$$ \Delta = 32^2 - 4 \cdot (9b^2 - 16)(-16 - 36b^2) = 0 $$

$$ 1024 - 4(9b^2 - 16)(-16 - 36b^2) = 0 $$

Dividimos ambos miembros entre 4 para simplificar:

$$ 256 - (9b^2 - 16)(-16 - 36b^2) = 0 $$

Desarrollamos el producto:

$$ 256 - 9b^2(-16 - 36b^2) + 16(-16 - 36b^2) = 0 $$

$$ 256 + 144b^2 + 324b^4 - 256 - 576b^2 = 0 $$

$$ 324b^4 - 432b^2 = 0 $$

$$ b^2 (324b^2 - 432) = 0 $$

La condición de tangencia se cumple cuando $ b^2 = 0 $ o bien $ b^2 = \frac{432}{324} = \frac{4}{3} $. Como el valor $ b^2 = 0 $ no tiene sentido en este contexto, tomamos:

$$ b^2 = \frac{4}{3} $$

$$ b = \sqrt{ \frac{4}{3} } = 2 \sqrt{ \frac{1}{3} } $$

Ya que conocemos los valores de los semiejes, $ a = 2 $ y $ b = 2 \sqrt{ \frac{1}{3} } $, los sustituimos en la ecuación canónica:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{4} - \frac{y^2}{\frac{4}{3}} = 1 $$

Multiplicamos el segundo término por el inverso del denominador:

$$ \frac{x^2}{4} - y^2 \cdot \frac{3}{4} = 1 $$

$$ \frac{x^2}{4} - \frac{3y^2}{4} = 1 $$

Multiplicamos ambos miembros por 4 para eliminar denominadores:

$$ x^2 - 3y^2 = 4 $$

Esta es la ecuación de la hipérbola con centro en el origen, tangente a la recta $ 2x - 3y - 2 = 0 $, y vértice real en $ A(2;0) $.

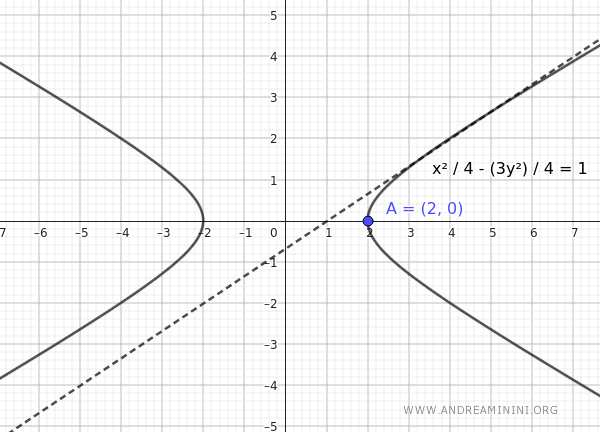
Y así se obtiene la ecuación buscada.