Ecuación de la Hipérbola

Aquí, \(a\) representa la distancia desde el centro \(O\) de la hipérbola hasta los vértices sobre el eje x, mientras que \(b\) corresponde a la distancia sobre el eje y, que determina la forma de la curva.

En ambos casos, la hipérbola se manifiesta como una curva abierta, simétrica respecto a los ejes coordenados y al origen, compuesta por dos ramas dispuestas simétricamente respecto a dichos ejes.

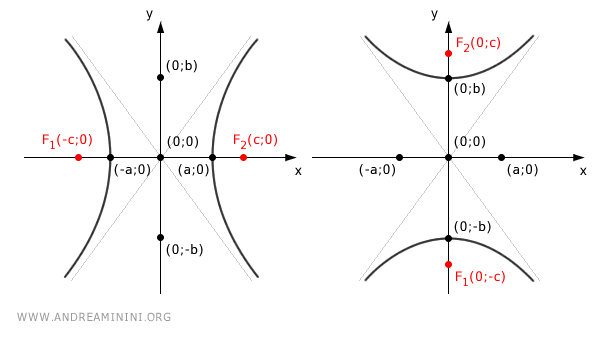
El centro de la hipérbola \((0, 0)\), en su forma estándar, es el punto de simetría desde el cual parten dos rectas llamadas asíntotas, hacia las cuales la hipérbola se aproxima sin llegar jamás a tocarlas.

Las ecuaciones de dichas asíntotas son:

$$ y = \pm \frac{b}{a} x $$

Estas rectas forman un ángulo con los ejes y definen la dirección en la que se extienden indefinidamente las ramas de la hipérbola.

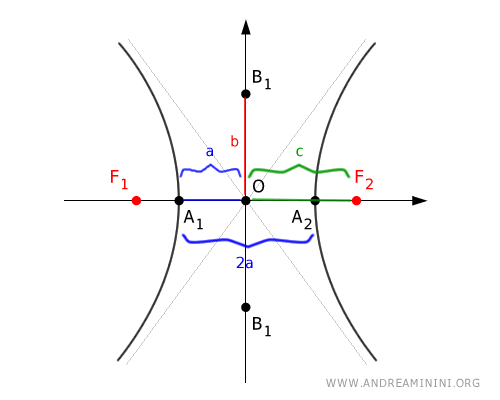
La hipérbola está constituida por dos ramas infinitas, cada una de las cuales se aproxima progresivamente a su asíntota correspondiente.

Los focos son dos puntos fijos situados sobre el eje x o el eje y, en el interior de las ramas de la hipérbola, tales que la diferencia absoluta de las distancias desde cualquier punto \(P(x;y)\) de la curva a ambos focos es constante e igual a \(2a\).

$$ | \overline{PF_1} - \overline{PF_2} | = 2a $$

Nota: Si los focos se encuentran sobre el eje y, la relación es $$ | \overline{PF_1} - \overline{PF_2} | = 2b $$

Las coordenadas de los focos son:

• Si los focos están sobre el eje x: $$ F_1(-c;0) $$ $$ F_2(c;0) $$
• Si los focos están sobre el eje y: $$ F_1(0;-c) $$ $$ F_2(0;c) $$

Aquí, \(c\) es la distancia del centro a cada foco, mientras que \(a\) y \(b\) son las distancias del centro a los vértices. Estos tres parámetros están relacionados por la fórmula:

$$ c = \sqrt{a^2+b^2} $$

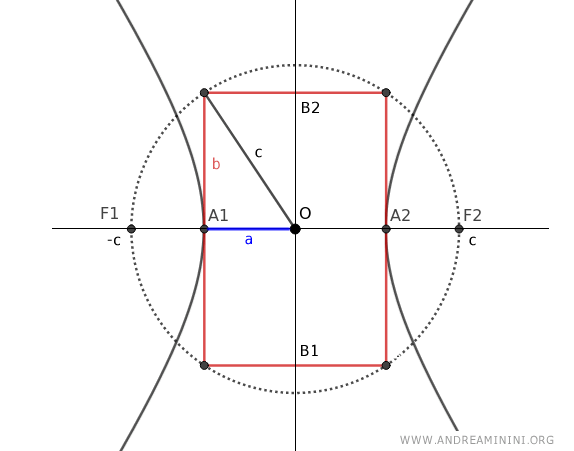
Explicación: Traza una circunferencia con centro en O y radio "c", junto con un rectángulo centrado en O de lados \(2a\) y \(2b\). Al construir un triángulo rectángulo con catetos "a" y "b" e hipotenusa "c", se obtiene, por el teorema de Pitágoras, que \(c^2 = a^2 + b^2\).

El eje que pasa por los focos se denomina eje transverso, mientras que el eje perpendicular a él se llama eje conjugado.

Los puntos donde la hipérbola corta al eje transverso se llaman vértices y sus coordenadas son:

• Si los focos están sobre el eje x: $$ A_1(-a;0) $$ $$ A_2(a;0) $$
• Si los focos están sobre el eje y: $$ B_1(0;-b) $$ $$ B_2(0;b) $$

Explicación: Para hallar los vértices cuando el eje transverso está sobre el eje x, se sustituye \(y = 0\) en la ecuación: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ $$ \frac{x^2}{a^2} - \frac{0^2}{b^2} = 1 $$ $$ \frac{x^2}{a^2} = 1 $$ $$ x^2 = a^2 $$ $$ x = a $$ Análogamente, si el eje transverso está sobre el eje y, se sustituye \(x = 0\): $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 $$ $$ \frac{0^2}{a^2} - \frac{y^2}{b^2} = -1 $$ $$ - \frac{y^2}{b^2} = -1 $$ $$ y^2 = b^2 $$ $$ y = b $$

Los vértices sobre el eje transverso se denominan vértices reales, mientras que los del eje conjugado se conocen como vértices imaginarios.

La excentricidad de la hipérbola se define como la razón entre la distancia focal \(c\) y la longitud del eje transverso \(a\) o \(b\), según el caso.

• Si el eje transverso es el eje x: $$ e = \frac{c}{a} $$
• Si el eje transverso es el eje y: $$ e = \frac{c}{b} $$

Dado que en toda hipérbola se cumple \(c > a\) si el eje transverso es horizontal (y \(a > 0\)), la excentricidad \(e = \frac{c}{a}\) es siempre mayor que 1 \((e > 1)\).

Nota. De igual modo, si el eje transverso está sobre el eje y, se tiene que \(c > b\) y \(b > 0\), por lo que también en este caso la excentricidad \(e = \frac{c}{b}\) cumple \(e > 1\).

Toda hipérbola tiene dos focos y dos directrices, que son simétricas, paralelas entre sí y perpendiculares al eje transverso.

Si el eje transverso (donde se ubican los focos) coincide con el eje \(x\), las directrices están dadas por:

$$ x = \pm \frac{a^2}{c} $$

En cambio, si el eje transverso está sobre el eje \(y\), las directrices son:

$$ y = \pm \frac{b^2}{c} $$

En general, como ocurre en toda sección cónica, para un punto \( P(x;y) \) de la hipérbola, la razón entre la distancia \( \overline{PF} \) al foco y la distancia \( \overline{PH} \) a la directriz es constante e igual a la excentricidad:

$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$

El siguiente ejemplo ilustra gráficamente el papel de las directrices en una hipérbola.

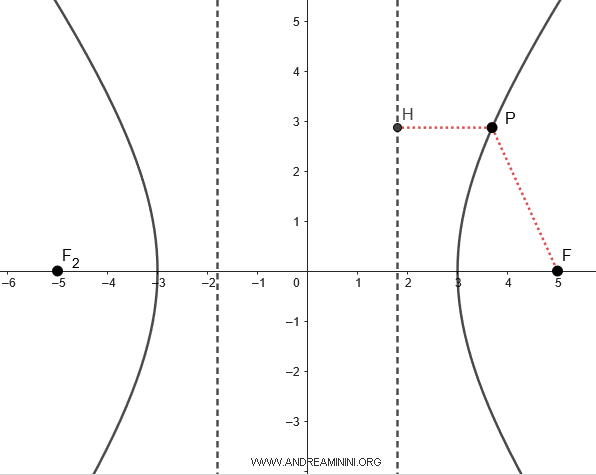
Demostración. Consideremos una hipérbola con eje transverso sobre el eje x: $$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$ Las directrices son perpendiculares al eje x y tienen la forma: $$ x = k $$ Según la definición, la razón entre la distancia de cualquier punto de la hipérbola al foco y su distancia a la directriz es constante e igual a la excentricidad: $$ \frac{ \overline{PF} }{ \overline{PH} } = e $$ donde \( e = \frac{c}{a} \). Tomando el vértice \( A(a,0) \) como punto \( P \), se tiene que \( \overline{PF} = c-a \) y \( \overline{PH} = a-k \). $$ \frac{ c-a }{ a-k } = \frac{c}{a} $$ Multiplicando ambos miembros por \(a(a-k)\): $$ a(c-a) = c(a-k) $$ $$ \require{cancel} \cancel{ac} - a^2 = \cancel{ac} - kc $$ $$ - a^2 \cdot (-1) = - kc \cdot (-1) $$ $$ a^2 = kc $$ $$ k = \frac{a^2}{c} $$ Por simetría, las directrices se ubican en \( (k;0) \) y \( (-k;0) \). Si el eje transverso está sobre el eje y, entonces las directrices se expresan como \( y = \pm \frac{b^2}{c} \).

Ejemplo práctico

Analicemos una hipérbola con \(a = 3\) y \(b = 4\), cuyos focos se encuentran sobre el eje x.

La ecuación de esta hipérbola es:

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

$$ \frac{x^2}{3^2} - \frac{y^2}{4^2} = 1 $$

$$ \frac{x^2}{9} - \frac{y^2}{16} = 1 $$

Para comprender mejor su comportamiento geométrico, representémosla en un sistema de coordenadas cartesianas.

Los vértices de la hipérbola se encuentran en los puntos \((\pm 3, 0)\).

Las asíntotas están definidas por las siguientes ecuaciones:

$$ y = \pm \frac{4}{3} x $$

Al trazar estas rectas y esbozar las ramas de la hipérbola que se acercan progresivamente a ellas, obtenemos su representación gráfica.

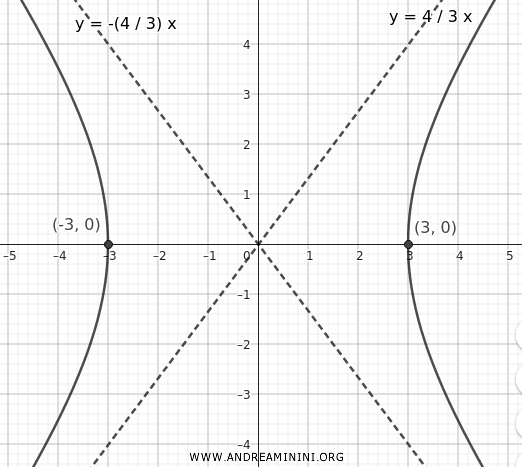
Dado que los focos están sobre el eje x, sus coordenadas son:

$$ F_1(-c;0) $$

$$ F_2(c;0) $$

Donde \(c\) se determina a partir de la relación:

$$ c^2 = a^2 + b^2 $$

$$ c = \sqrt{a^2 + b^2} $$

Como \(a^2 = 9\) y \(b^2 = 16\), resulta:

$$ c = \sqrt{9 + 16} = \sqrt{25} = 5 $$

Por tanto, los focos se ubican en:

$$ F_1(-5;0) \qquad F_2(5;0) $$

Esta es su representación gráfica:

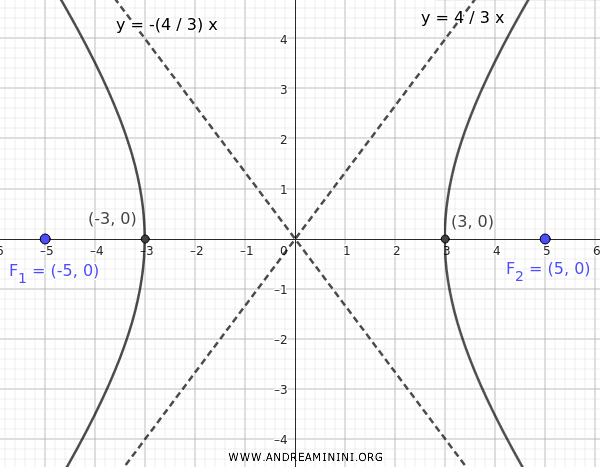
En este caso, el eje transverso - que contiene a los focos - coincide con el eje x.

Las directrices se expresan mediante:

$$ x = \pm \frac{a^2}{c} $$

Con \( a = 3 \) y \( c = 5 \), se obtiene:

$$ x = \pm \frac{9}{5} = \pm 1.8 $$

La razón entre las distancias \( \overline{PF} \) (del punto al foco) y \( \overline{PH} \) (del punto a la directriz) permanece constante para cualquier punto \( P(x;y) \) de la hipérbola y coincide con la excentricidad \( e \):

$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$

Por ejemplo, si en un punto \(P\) se verifica \( \overline{PF} = 4.09 \) y \( \overline{PH} = 2.46 \), entonces:

$$ e = \frac{4.09}{2.46} \approx 1.67 $$

Por tanto, la excentricidad de esta hipérbola es aproximadamente \( e \approx 1.67 \), y esta proporción se cumple en cualquier otro punto de la curva.

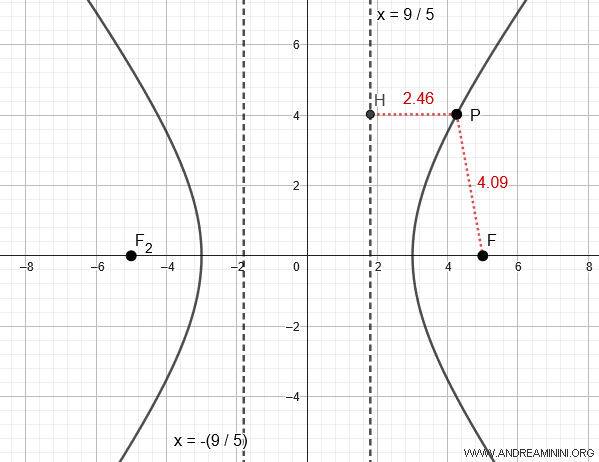
Nota: También puede obtenerse la excentricidad aplicando directamente la fórmula $$ e = \frac{c}{a} = \frac{5}{3} \approx 1.67 $$. El valor final es coherente.

La demostración

Supongamos que los focos \(F_1(-c;0)\) y \(F_2(c;0)\) están sobre el eje x, y que el centro de la hipérbola coincide con el origen del sistema cartesiano.

Para deducir su ecuación estándar, consideramos un punto arbitrario \(P(x;y)\) perteneciente a la curva.

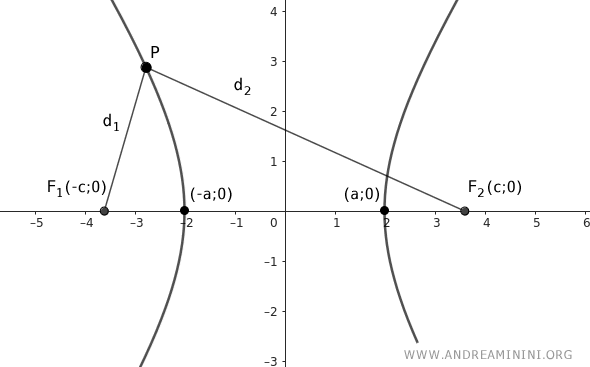
En una hipérbola, la diferencia entre las distancias a los focos es igual a \(2a\):

$$ \overline{PF_1} - \overline{PF_2} = 2a $$

¿Por qué esta diferencia es igual a \(2a\)? Porque, por definición, para cualquier punto de una hipérbola, la diferencia absoluta de distancias a los focos es constante. Los focos se hallan a una distancia \(c\) del centro.

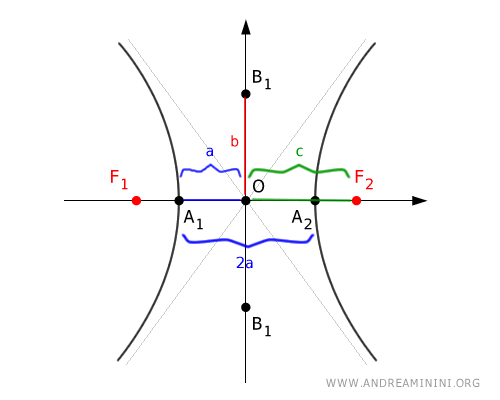
Si tomamos el vértice \(A_2\), sus distancias a los focos son: $$ \overline{A_2F_2} = c-a \qquad \overline{A_2F_1} = a+c $$ Restando: $$ \overline{A_2F_1} - \overline{A_2F_2} = (a+c)-(c-a) = 2a $$

Retomando el punto \(P(x;y)\):

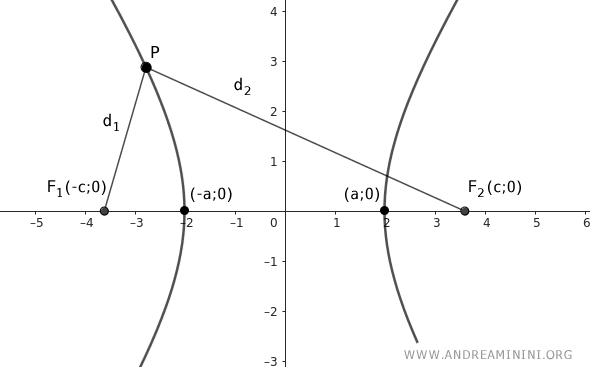
Aplicamos el teorema de Pitágoras para calcular las distancias desde P a los focos:

$$ \overline{PF_1} = \sqrt{(x+c)^2 + y^2} \qquad \overline{PF_2} = \sqrt{(x-c)^2 + y^2} $$

La diferencia de distancias queda entonces:

$$ \sqrt{(x+c)^2 + y^2} - \sqrt{(x-c)^2 + y^2} = 2a $$

Despejamos una raíz:

$$ \sqrt{(x+c)^2 + y^2} = 2a + \sqrt{(x-c)^2 + y^2} $$

Elevamos ambos miembros al cuadrado:

$$ (x+c)^2 + y^2 = 4a^2 + 4a \sqrt{(x-c)^2 + y^2} + (x-c)^2 + y^2 $$

Simplificamos y desarrollamos:

$$ x^2 + 2xc + c^2 = 4a^2 + 4a \sqrt{(x-c)^2 + y^2} + x^2 - 2xc + c^2 $$

$$ 2xc = 4a^2 + 4a \sqrt{(x-c)^2 + y^2} - 2xc $$

$$ 4xc - 4a^2 = 4a \sqrt{(x-c)^2 + y^2} $$

Dividimos entre 4:

$$ xc - a^2 = a \sqrt{(x-c)^2 + y^2} $$

Volvemos a elevar al cuadrado:

$$ (xc - a^2)^2 = a^2[(x-c)^2 + y^2] $$

Desarrollamos ambos miembros:

$$ x^2c^2 - 2xca^2 + a^4 = x^2a^2 - 2xca^2 + a^2c^2 + a^2y^2 $$

Simplificamos:

$$ x^2c^2 + a^4 = x^2a^2 + a^2c^2 + a^2y^2 $$

Dividimos entre \(a^2\):

$$ \frac{x^2c^2}{a^2} + a^2 = x^2 + c^2 + y^2 $$

Reagrupamos:

$$ x^2\left( \frac{c^2}{a^2} - 1 \right) - y^2 = c^2 - a^2 $$

Como \(c^2 - a^2 = b^2\), obtenemos:

$$ x^2 \cdot \frac{b^2}{a^2} - y^2 = b^2 $$

Multiplicamos por \( \frac{1}{b^2} \):

$$ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $$

Explicación: Al construir un rectángulo centrado en la hipérbola con lados \(2a\) y \(2b\), y trazar su diagonal, se forma un triángulo rectángulo cuya hipotenusa es \(c\) y cuyos catetos son \(a\) y \(b\). Por el teorema de Pitágoras, \(c^2 = a^2 + b^2\), de donde se deduce que \(c^2 - a^2 = b^2\).

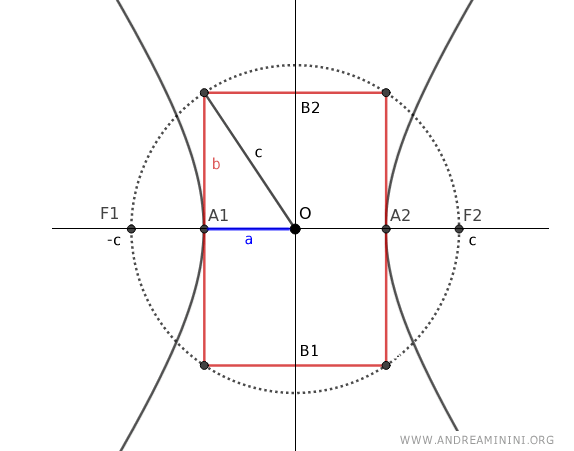
Así obtenemos la ecuación estándar de la hipérbola con focos sobre el eje x y centro en el origen \(O(0;0)\) del sistema cartesiano.

Y se puede continuar a partir de aquí.