La distancia entre dos puntos
La distancia es el trayecto más corto que une dos puntos. Para calcular la distancia euclidiana entre dos puntos en el plano, se aplica el teorema de Pitágoras: $$ \overline{AB} = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2} $$
Aquí, (x1, y1) y (x2, y2) son las coordenadas cartesianas de los puntos A y B en el plano.
Un ejemplo práctico
Veamos las coordenadas cartesianas de dos puntos en el plano:
$$ A = \begin{pmatrix} 2 \\ 4 \end{pmatrix} = (2, 4) $$
$$ B = \begin{pmatrix} 6 \\ 1 \end{pmatrix} = (6, 1) $$
La distancia entre estos dos puntos se determina así:
$$ \overline{AB} = \sqrt{(6-2)^2+(1-4)^2} $$
$$ \overline{AB} = \sqrt{4^2+(-3)^2} = \sqrt{16+9} = \sqrt{25} = 5 $$
Verifícalo con Geogebra. El valor obtenido coincide con el resultado mostrado en Geogebra.
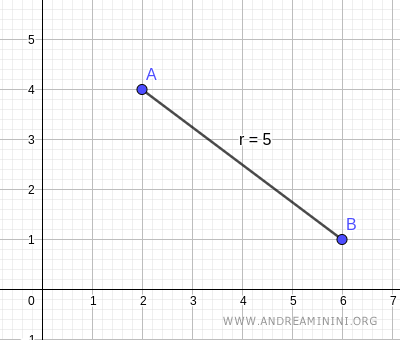
La demostración
Consideremos dos puntos en el plano:
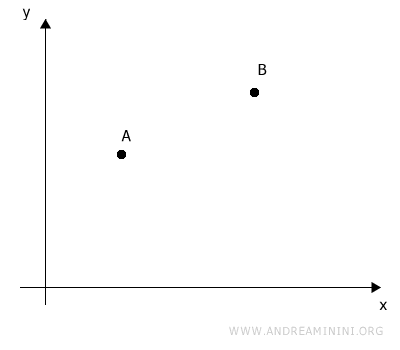
El segmento AB representa la distancia que separa los puntos A y B.
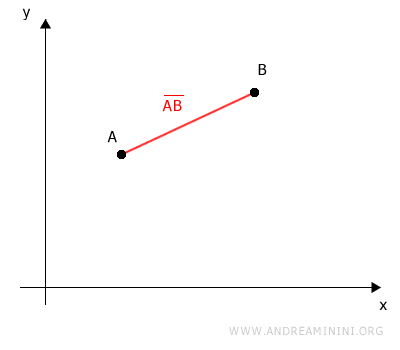
Proyectamos ambos puntos sobre los ejes cartesianos.
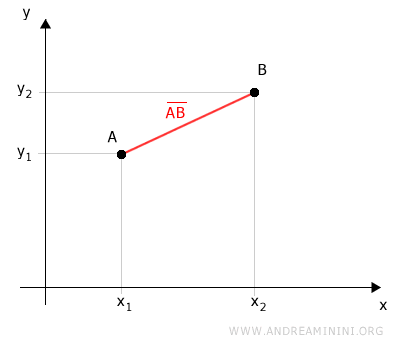
Estas proyecciones generan un triángulo rectángulo ABC en el plano.
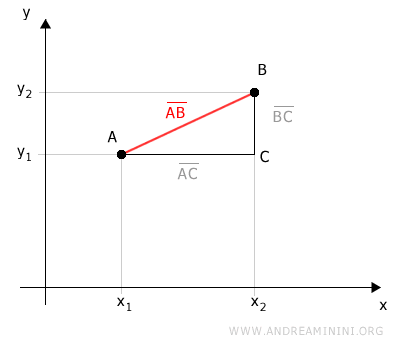
El segmento AB es la hipotenusa de dicho triángulo rectángulo ABC.
Por tanto, para calcular la longitud de AB podemos emplear el teorema de Pitágoras.
$$ \overline{AB} = \sqrt{\overline{AC}^2 + \overline{BC}^2} $$
El segmento AC es la proyección de AB sobre el eje x.
$$ \overline{AB} = \sqrt{(x_2-x_1)^2 + \overline{BC}^2} $$
El segmento BC es la proyección de AB sobre el eje y.
$$ \overline{AB} = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2} $$
Esta es, precisamente, la fórmula que queríamos demostrar.
Distancia entre dos puntos en el espacio
Si tenemos dos puntos A $(x_A,\,y_A,\,z_A)$ y B $(x_B,\,y_B,\,z_B)$ en el espacio cartesiano, la distancia $AB$ se calcula mediante: $$ AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2}$$
La distancia entre dos puntos en el espacio equivale a la longitud de la diagonal de un paralelepípedo rectangular cuyas aristas miden las diferencias absolutas en cada eje: $|x_A-x_B|$, $|y_A-y_B|$ y $|z_A-z_B|$.
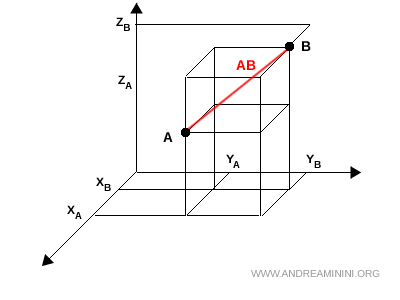
En otras palabras, para hallar la distancia entre los puntos $ A $ y $ B $, se utiliza la misma fórmula con la que se obtiene la longitud de la diagonal $ AB $ de dicho paralelepípedo.
Nota. Si uno de los puntos coincide con el origen $O(0,0,0)$, la fórmula se reduce al módulo del vector de posición del otro punto. Por ejemplo, para calcular la distancia del punto $ A $ al origen $ O $, se usa: $$ AO=\sqrt{x_A^2+y_A^2+z_A^2} $$
Ejemplo
Consideremos estos dos puntos en el espacio:
$$ A(2,\,-1,\,3)$$
$$ B(-2,\,4,\,0) $$
La distancia entre ellos se calcula así:
$$ AB=\sqrt{(x_A-x_B)^2+(y_A-y_B)^2+(z_A-z_B)^2} $$
$$ AB=\sqrt{(2-(-2))^2+((-1)-4)^2+(3-0)^2} $$
$$ AB=\sqrt{4^2+(-5)^2+3^2} $$
$$ AB=\sqrt{16+25+9} $$
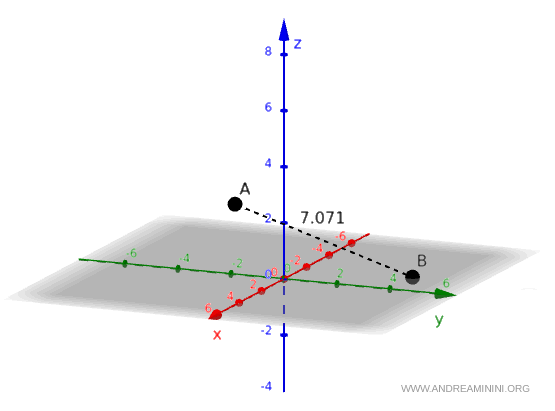
$$ AB=\sqrt{50} \approx 7.071 $$
Por tanto, la distancia entre ambos puntos es $ \sqrt{50} $.
Distancia calculada con coordenadas polares
La distancia entre dos puntos en el plano también puede determinarse a partir de sus coordenadas polares mediante la fórmula: $$ \overline{AB} = \sqrt{r_1^2 + r_2^2 - 2r_1r_2 \cos (\alpha_2 - \alpha_1)} $$
Donde (r1, α1) y (r2, α2) son las coordenadas polares de los puntos.
Ejemplo
Dos puntos en el plano tienen las siguientes coordenadas polares:
$$ A [ \ 4.47 \ , \ 63.43° \ ] $$
$$ B [ \ 6.08 \ , \ 9.46° \ ] $$
Gráficamente, se representa de esta forma:
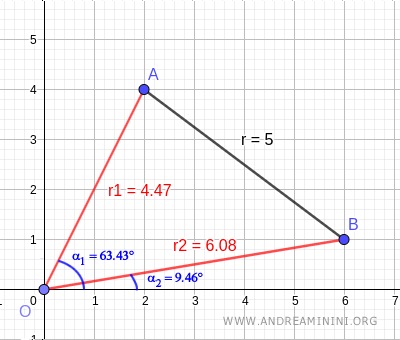
La distancia entre A y B resulta ser:
$$ \overline{AB} = \sqrt{r_1^2 + r_2^2 - 2r_1r_2 \cos (\alpha_2 - \alpha_1)} $$
$$ \overline{AB} = \sqrt{(4.47)^2 + (6.08)^2 - 2 \cdot (4.47) \cdot (6.08) \cos (9.46° - 63.43°)} $$
$$ \overline{AB} = \sqrt{19.98 + 36.97 - 54.36 \cdot \cos (-53.97°)} $$
$$ \overline{AB} = \sqrt{25} = 5 $$
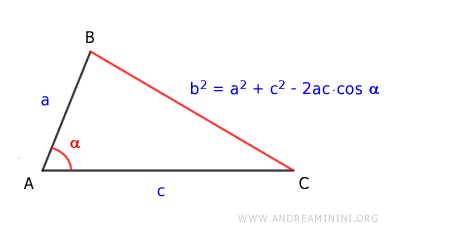
Demostración. Esta fórmula para calcular distancias en coordenadas polares se deduce de la ley de cosenos en un triángulo.
Y así sucesivamente.