Rectas cortadas por una transversal
Cuando dos rectas distintas r y s son cortadas por una recta transversal t en dos puntos, se forman ocho ángulos en el plano.
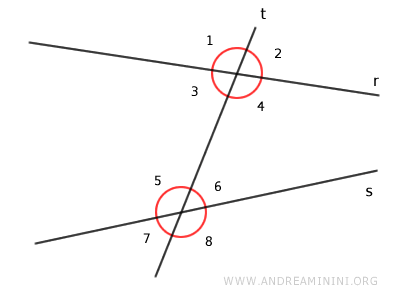
La denominación de estos ángulos varía en función de su posición respecto a las rectas.
Para empezar, los ángulos se clasifican en dos grupos: ángulos interiores y ángulos exteriores.
- Ángulos interiores
Son los ángulos situados en la zona comprendida entre las dos rectas r y s.
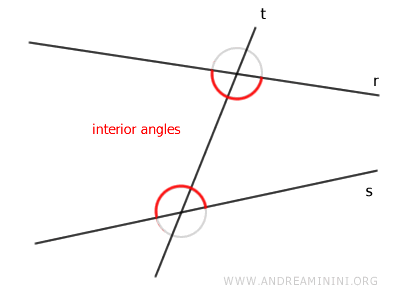
- Ángulos exteriores
Son los ángulos que se encuentran fuera del espacio comprendido entre las dos rectas.
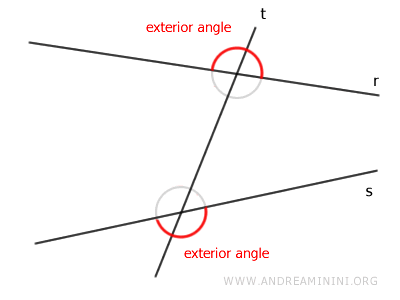
En total, se forman cuatro ángulos interiores y cuatro ángulos exteriores.
Según su disposición respecto a la transversal, los ángulos se agrupan en alternos, consecutivos o correspondientes.
- Ángulos alternos
Los ángulos alternos no son adyacentes y se encuentran a lados opuestos de la transversal. Ambos deben pertenecer a la misma categoría: o bien son los dos interiores, o bien los dos exteriores. Si uno es interior, el otro también lo es.
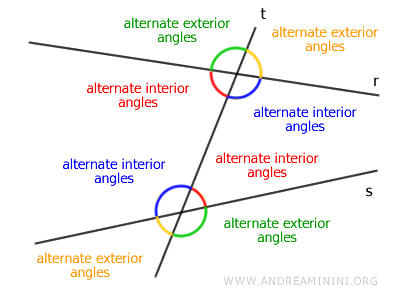
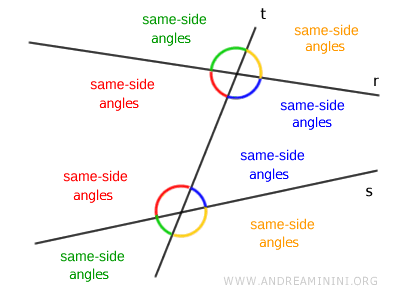
- Ángulos del mismo lado
Los ángulos del mismo lado, también llamados ángulos consecutivos, no son adyacentes y se sitúan en el mismo lado de la transversal. Al igual que ocurre con los alternos, deben ser ambos interiores o ambos exteriores.
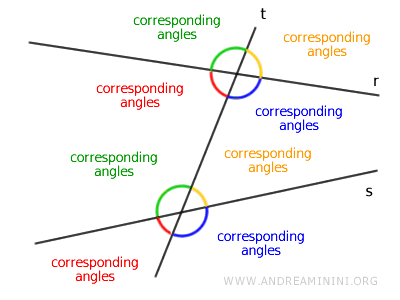
- Ángulos correspondientes
Los ángulos correspondientes no son adyacentes y se localizan en el mismo lado de la transversal. En este caso, uno es interior y el otro es exterior.
Y así sucesivamente.