Rectas perpendiculares

Se denominan rectas perpendiculares a dos rectas secantes que dividen el plano en cuatro ángulos rectos de 90°.

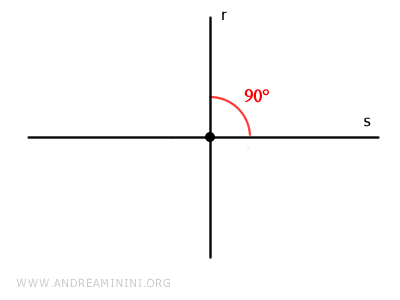
Para indicar que dos rectas son perpendiculares, se utiliza el símbolo de la T invertida: $$ r \perp s $$

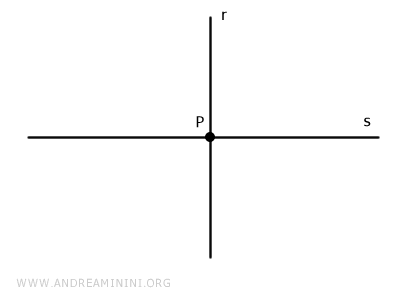
Consideremos dos rectas distintas, r y s, en un plano.

Estas rectas son rectas secantes porque se cruzan en un único punto P, conocido como el "pie de la perpendicular".

La intersección de ambas rectas divide el plano cartesiano en cuatro regiones y forma cuatro ángulos.

Si uno de esos ángulos es recto (90°), automáticamente los otros tres también lo son.

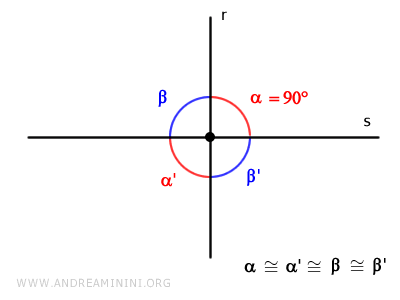
En tal caso, se dice que las dos rectas son perpendiculares entre sí.

Explicación: Para dos rectas secantes, los ángulos opuestos por el vértice son congruentes, es decir, α≅α' y β ≅β'. $$ \alpha \cong \alpha ' $$ $$ \beta \cong \beta ' $$ Por tanto, si uno de los ángulos es recto, es decir α=90°, su opuesto α' también mide 90° al ser congruente. $$ \alpha = \alpha ' = 90° $$ La suma de ambos ángulos es α+α'=180°. $$ \alpha + \alpha' = 90° + 90° = 180° $$ Como la suma de los ángulos alrededor de un punto es 360°, los ángulos restantes β+β' también deben sumar 180°. $$ \alpha + \alpha ' + \beta + \beta ' = 360° $$ $$ \beta + \beta ' = 360° - ( \alpha + \alpha' ) = 360° - 180° = 180° $$ Los ángulos β y β' son congruentes (β≅β') al ser opuestos por el vértice, de modo que cada uno mide 90°. $$ \beta = \beta ' = \frac{180°}{2} = 90° $$ Por lo tanto, los cuatro ángulos formados son congruentes y miden 360°/4 = 90°.

Dada una recta r y un punto P exterior a ella, existe una única recta que pasa por el punto P y es perpendicular a la recta r.

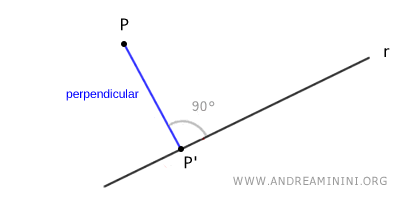
Cuando una recta corta a otra sin formar un ángulo recto, se denomina “recta oblicua”.

¿Cómo se puede verificar si dos rectas son perpendiculares?

En geometría analítica, dos rectas $ y=mx+q $ y $ y=m'x+q' $ son perpendiculares si el producto de sus pendientes es igual a -1:

$$ m \cdot m' = -1 $$

Alternativamente, si las ecuaciones están en forma implícita, dos rectas $ ax+by+c=0 $ y $ a'x+b'y+c'=0 $ son perpendiculares si cumplen la condición de perpendicularidad:

$$ aa'+ bb' = 0 $$

Esta condición es aplicable incluso si las rectas son paralelas a alguno de los ejes cartesianos.

En todos los casos, ambas condiciones permiten comprobar si dos rectas son perpendiculares y se utilizan en función de la forma en la que se expresen sus ecuaciones: $$ r \perp s \ \Longleftrightarrow \ m \cdot m' = -1 \  \Longleftrightarrow \ aa'+bb'= 0 $$

Las pendientes de las rectas perpendiculares

Dos rectas son perpendiculares si, y solo si, el producto de sus pendientes, m y m', es igual a -1: $$ m \cdot m' = -1 $$ es decir, $$ m = - \frac{1}{m'} $$

Dos rectas $ y=mx+q $ y $ y=m'x+q' $ son rectas perpendiculares si se intersectan en un punto formando un ángulo recto de 90°.

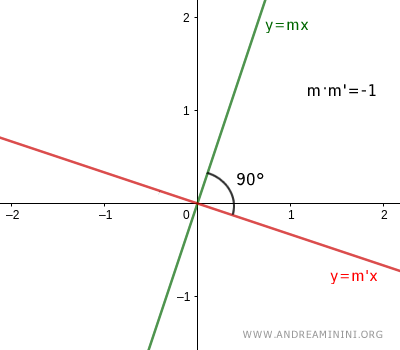
Cuando dos rectas son perpendiculares, el producto de sus pendientes es igual a -1:

$$ m \cdot m' = -1 $$

Por lo tanto, las pendientes de dos rectas perpendiculares son recíprocas y opuestas entre sí:

$$ m = - \frac{1}{m'} $$

Este teorema se cumple únicamente cuando ninguna de las rectas es paralela a los ejes.

Nota: Si una de las rectas es paralela al eje x, su pendiente es cero (m=0), y su recíproco opuesto, -1/m, implicaría dividir entre cero. Si una recta es paralela al eje y, no se puede calcular su pendiente con la fórmula m = y/x. Por lo tanto, en ambos casos, el teorema no resulta aplicable.

El enunciado inverso también es cierto.

Dos rectas cuyas pendientes cumplen que m·m' = -1 son perpendiculares.

Ejemplo práctico

Consideremos dos rectas perpendiculares:

$$ r = 2x $$

$$ r'= -\frac{1}{2} x $$

Ambas rectas se cortan en el origen y forman un ángulo recto de 90°.

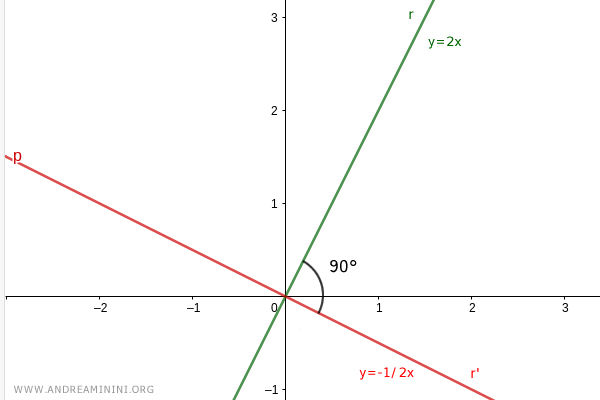
Las pendientes de ambas rectas son recíprocas y opuestas:

$$ m=2 $$

$$ m' = - \frac{1}{2} $$

Ejemplo 2

Veamos ahora dos rectas cuyas pendientes son recíprocas y opuestas:

$$ r = 3x $$

$$ r'= -\frac{1}{3} x $$

Representemos ambas rectas en el plano.

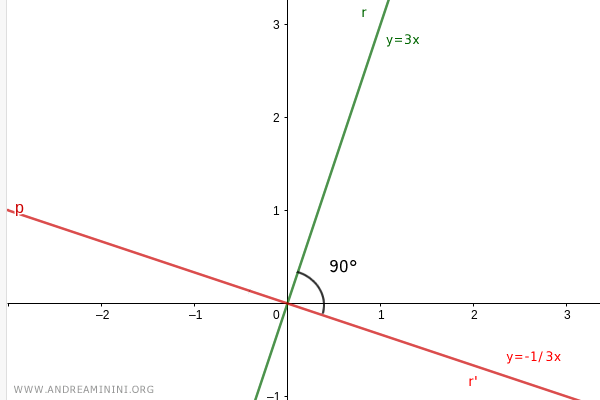
El ángulo que forman es recto.

Por tanto, las dos rectas son perpendiculares.

Demostración

Consideremos dos rectas perpendiculares, r y r', que no son paralelas a los ejes cartesianos:

$$ r: \ y=mx+q $$ $$ r': \ y=m'x+q' $$

Al ser perpendiculares, ambas rectas se intersectan en un punto, formando cuatro ángulos rectos de 90°.

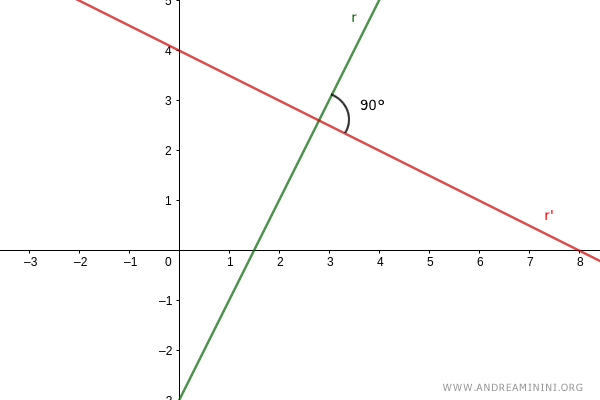
Para simplificar los cálculos, consideremos las rectas paralelas a r y r' que pasan por el origen (es decir, con q=0 y q'=0).

Al ser paralelas, mantienen las mismas pendientes m y m' que las rectas originales.

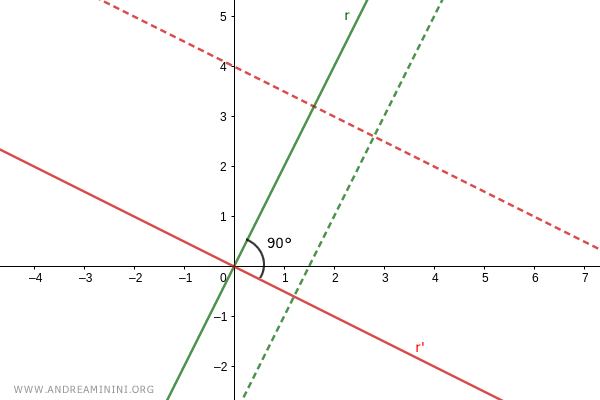
Tomemos un punto A=(x_A;y_A) sobre la recta r, con x_A=1.

Su proyección sobre el eje x determina un segmento de longitud AB.

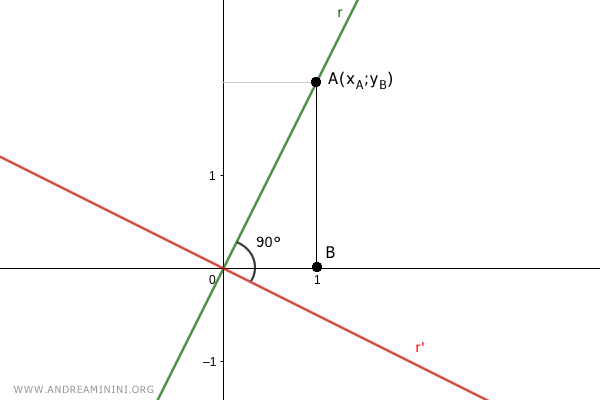
Sea C un punto sobre el eje x que se encuentra a la misma distancia del origen, de modo que OC=AB.

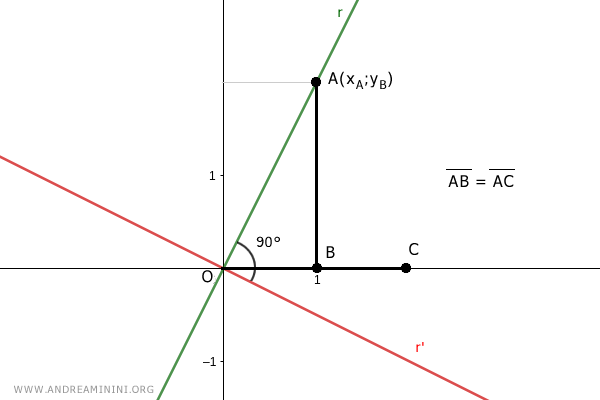
Desde el punto C se traza una perpendicular que corta a la recta r' en el punto D=(x_D;y_D).

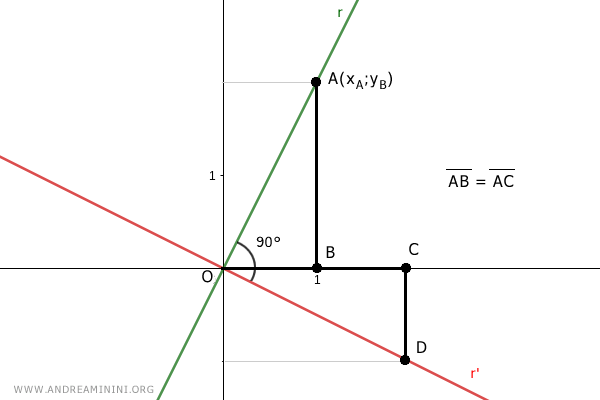
Los dos triángulos rectángulos OAB y OCD tienen en común el lado AB=OC, por construcción.

Ambos son triángulos rectángulos, pues poseen un ángulo de 90°.

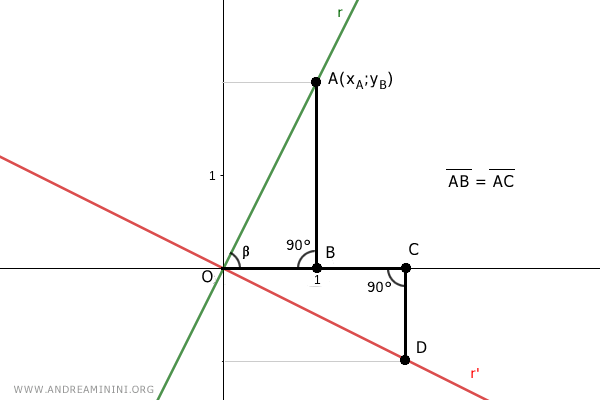
Además, los ángulos α y α' en ambos triángulos son complementarios respecto al ángulo β.

Por lo tanto, se cumple que α = α', es decir, tienen la misma medida.

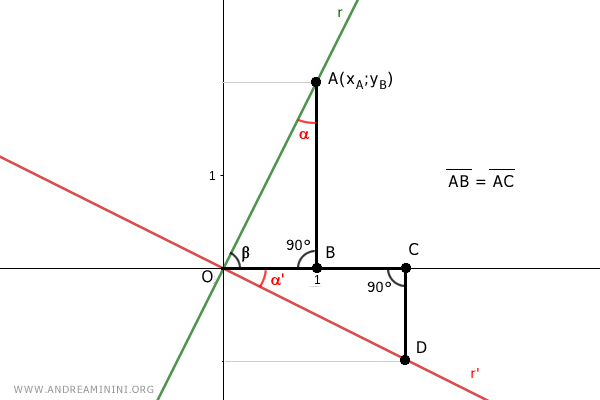
Como en todo triángulo rectángulo, la suma de sus ángulos es 180°, de modo que el tercer ángulo también coincide en ambos triángulos.

Así, los triángulos OAB y OCD son congruentes, ya que tienen ángulos iguales y un lado correspondiente congruente, AB≅OC.

En consecuencia, todos sus lados son iguales, siendo especialmente útil saber que OA=CD:

$$ \overline{OA} = {CD} $$

Como OA=1 por construcción, resulta que CD=1 también.

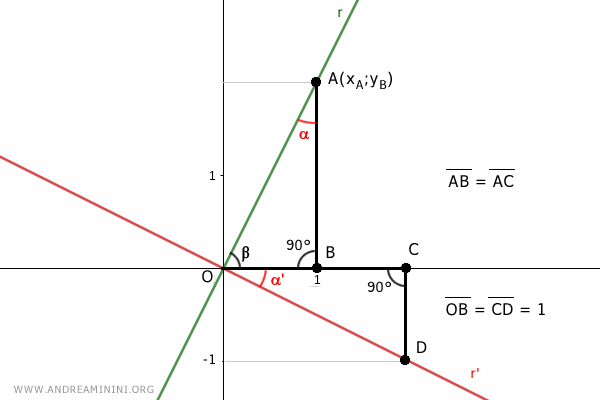
Si el segmento CD=1, entonces el punto D se ubica en las coordenadas D(x_D, -1).

Así, las coordenadas de los puntos A y D son:

$$ A=(1;y_A) $$

$$ D=(x_D;-1) $$

Con estas coordenadas, podemos calcular las pendientes de las rectas r y r':

$$ m = \frac{y_A}{x_A} = \frac{y_A}{1} = y_A $$

$$ m' = \frac{y_D}{x_D} = \frac{-1}{x_D} $$

Como AB=OC, se deduce que y_A=x_D.

Por tanto, las pendientes son recíprocas y de signo opuesto:

$$ m = y_A $$

$$ m' = - \frac{1}{y_A} $$

Demostración alternativa

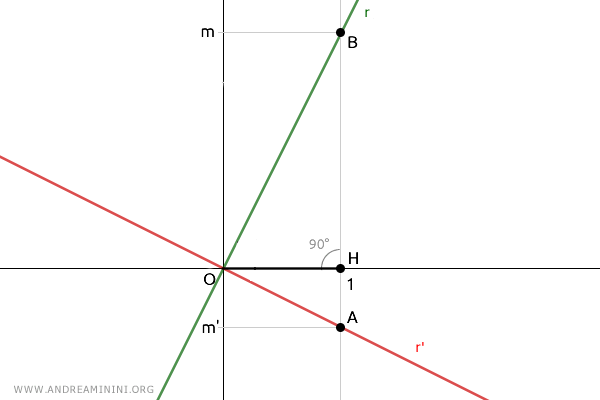
Supongamos dos rectas perpendiculares, r y r', que pasan por el origen del plano O.

Se traza un segmento unitario, OH=1, sobre el eje x positivo.

Después, se dibuja una recta perpendicular al eje x que pasa por el punto H, situado en las coordenadas (1;0).

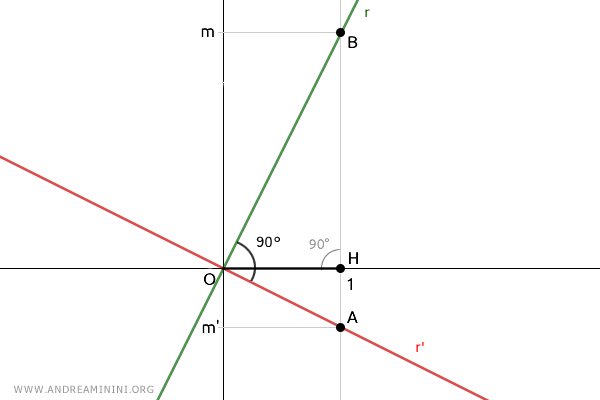
Esto permite determinar las pendientes de las dos rectas:

$$ m = \frac{ \overline{BH}}{ \overline{OH}} $$

$$ m' = \frac{ \overline{AH}}{ \overline{OH}} $$

Como OH=1 por construcción:

$$ m = \frac{ \overline{BH}}{ \overline{OH}} = \frac{ \overline{BH}}{1} = \overline{BH} $$

$$ m' = \frac{ \overline{AH}}{ \overline{OH}} = \frac{ \overline{AH}}{1} = \overline{AH} $$

De este modo, las pendientes m y m' coinciden con las longitudes de los segmentos $ \overline{BH} $ y $ \overline{AH} $.

 

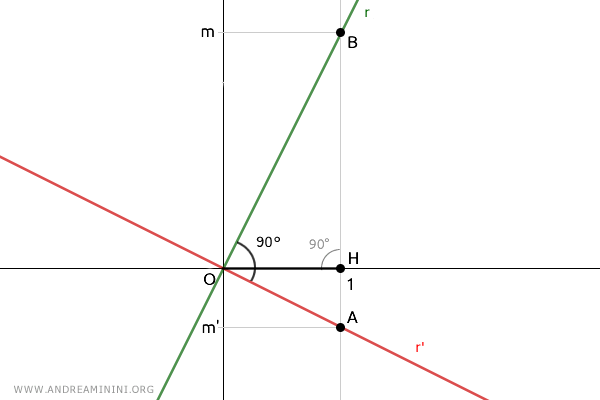
El triángulo OAB es un triángulo rectángulo, ya que los segmentos OA y OB se apoyan sobre las rectas r' y r respectivamente, que por hipótesis son perpendiculares, formando un ángulo recto de 90°.

Además, el segmento OH es la altura del triángulo OAB, pues es perpendicular al lado AB.

Según el segundo teorema de Euclides, el cuadrado de la altura relativa a la hipotenusa $ \overline{OH}^2 $ es igual al producto de las proyecciones de los catetos sobre la hipotenusa, es decir, $ \overline{AH} \cdot \overline{BH} $:

$$ \overline{OH}^2 = \overline{AH} \cdot \overline{BH} $$

Como sabemos que OH=1:

$$ 1^2 = \overline{AH} \cdot \overline{BH} $$

$$ 1 = \overline{AH} \cdot \overline{BH} $$

Además, dado que AH=|m'| y BH=|m|:

$$ 1 = | m | \cdot |m'| $$

Por lo tanto, el producto de los valores absolutos de las pendientes m y m' es igual a 1.

Como las rectas son perpendiculares, el producto de sus pendientes es negativo.

Esto se observa en el gráfico, donde m y m' tienen signos opuestos.

En este caso, m corresponde al semieje positivo de y y es positiva (m>0), mientras que m' corresponde al semieje negativo de y (m<0).

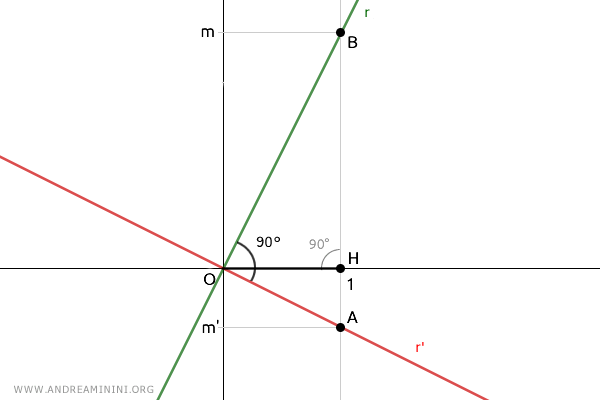
Por tanto, eliminando el valor absoluto, se concluye que el producto de las pendientes es -1:

$$ -1 = m \cdot m' $$

Con esto queda demostrada la afirmación.

Nota: Esta demostración también es válida si las rectas perpendiculares, s y s', no pasan por el origen: $$ s: \ y = mx+q $$ $$ s': \ y = m'x+q' $$ ya que podemos considerar sus rectas paralelas s||r y s'||r', que sí pasan por el origen (0,0): $$ r: \ y = mx $$ $$ r': \ y = m'x $$  Si s y s' son perpendiculares, entonces sus paralelas r y r' también lo son.

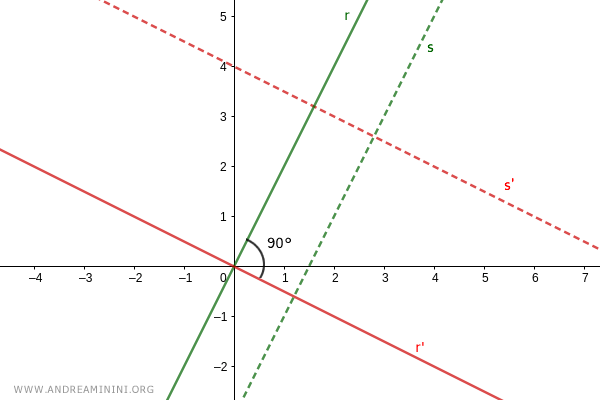
Demostración inversa

En este caso, partimos de la hipótesis de que el producto de las pendientes de dos rectas es igual a -1:

$$ m \cdot m' = -1 $$

Se traza un segmento OH=1 y se construye el triángulo OAB:

Para demostrar que las rectas r y r' son perpendiculares, se aplica el recíproco del segundo teorema de Euclides: 

Si en un triángulo el cuadrado de la altura es igual al producto de las longitudes de los dos segmentos en que la altura divide el lado opuesto, entonces el triángulo es rectángulo y el vértice (C) desde donde parte la altura forma un ángulo recto de 90°.

$$ \overline{OH}^2 = \overline{AH} \cdot \overline{BH} $$

En este caso, AH=|m'| y BH=|m|, ya que las pendientes se toman en valor absoluto por tratarse de longitudes:

$$ \overline{OH}^2 = \left| - \frac{1}{m} \right| \cdot |m| $$

$$ \overline{OH}^2 = 1 $$

Como OH=1 por construcción, la igualdad se cumple.

Por lo tanto, según el recíproco del segundo teorema de Euclides, el ángulo desde el que parte la altura OH es recto (90°) y el triángulo OAB es un triángulo rectángulo.

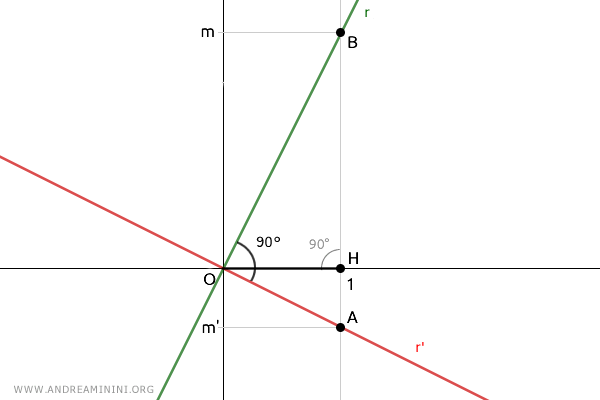
Si los segmentos OA y OB son perpendiculares (90°), entonces las rectas r' y r sobre las que se apoyan también lo son.

Queda así demostrado que las rectas r y r' son perpendiculares entre sí.

La condición de perpendicularidad

Dos rectas $ ax+by+c=0 $ y $ a'x+b'y+c'=0 $ son perpendiculares si cumplen la siguiente condición de perpendicularidad: $$ aa' + bb' = 0 $$

Una de las ventajas de esta condición es que permite verificar si dos rectas son perpendiculares incluso cuando alguna de ellas es paralela a los ejes cartesianos.

Ejemplo

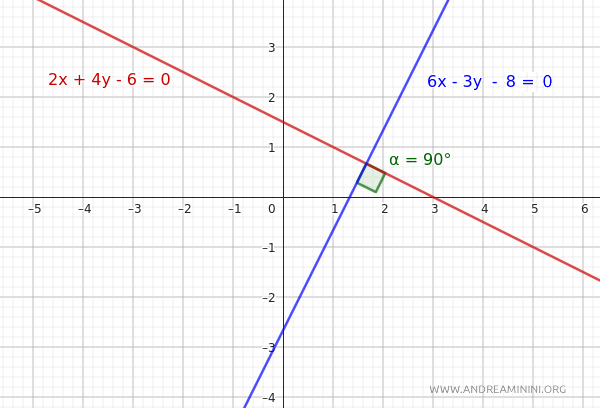
Consideremos dos rectas cuyas ecuaciones están expresadas en forma implícita:

$$ r: 2x+4y-6=0 $$

$$ r': 6x-3y-8=0 $$

Para determinar si son perpendiculares, aplicamos la condición de perpendicularidad:

$$ aa'+bb'=0 $$

En este caso, los coeficientes de la primera recta son a=2 y b=4, mientras que los de la segunda son a'=6 y b'=-3:

$$ 2 \cdot 6 + 4 \cdot (-3)=0 $$

$$ 12 -12 =0 $$

$$ 0 =0 $$

La condición se cumple, por lo que las rectas r y r' son perpendiculares.

Nota: Para comprobar rápidamente si dos rectas son perpendiculares sin necesidad de graficarlas, se pueden escribir sus ecuaciones en forma implícita, una debajo de la otra, alineando las variables x e y en columnas, y calcular mentalmente la suma algebraica de los productos de los coeficientes correspondientes. Si el resultado es cero, las rectas son perpendiculares.

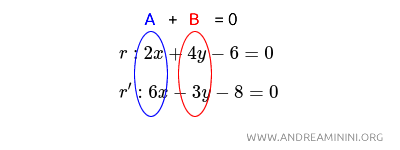
Por ejemplo, en este caso, A=2·6 y B=4·(-3), es decir, A=12 y B=-12. La suma algebraica de los productos es A+B=12+(-12)=0. El resultado es cero, lo que confirma que las rectas son perpendiculares.

Demostración

Consideremos dos rectas, r y s, en forma implícita:

$$ ax+by+c=0 $$

$$ a'x+b'y+c'=0 $$

Las pendientes de ambas rectas se determinan así:

$$ m = - \frac{a}{b} $$

$$ m' = - \frac{a'}{b'} $$

Si dos rectas son perpendiculares, el producto de sus pendientes es igual a -1:

$$ m \cdot m' = -1 $$

$$ m = \frac{-1}{m'} $$

Sustituyamos m=-a/b y m'=-a'/b':

$$ - \frac{a}{b} = \frac{-1}{\left( - \frac{a'}{b'} \right)} $$

$$ - \frac{a}{b} = \frac{1}{\frac{a'}{b'}} $$

$$ - \frac{a}{b} = \frac{b'}{a'} $$

Multiplicamos en cruz:

$$ - aa' = bb' $$

$$ - aa' - bb' = 0 $$

Multiplicamos por -1 en ambos miembros:

$$ aa' + bb' = 0 $$

Así queda demostrada la condición de perpendicularidad.

Recta perpendicular a un plano

Se dice que una recta \( r \) es perpendicular a un plano \( \alpha \) si lo corta y es perpendicular a todas las rectas contenidas en dicho plano.

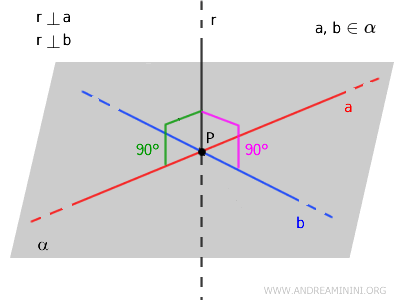
En términos más sencillos, una recta es perpendicular a un plano \( \alpha \) si cumple dos condiciones:

• La recta \( r \) corta al plano \( \alpha \) en un único punto; es decir, es incidente al plano.
• La recta \( r \) es perpendicular a todas las rectas contenidas en el plano \( \alpha \) que pasan por el punto de intersección.

Esto equivale a decir que el vector dirección de la recta \( r \) es paralelo al vector normal del plano \( \alpha \).

Cuando una recta corta a un plano sin ser perpendicular, se la denomina recta oblicua.

Observaciones

Algunas observaciones adicionales sobre las rectas perpendiculares:

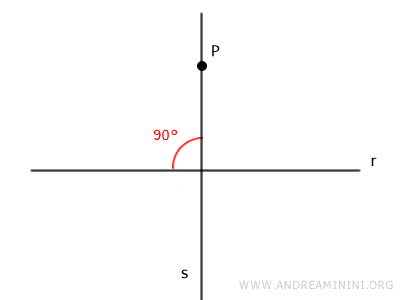
• Teorema de la perpendicular
  Dado un punto P y una recta r en el plano, existe una única recta s que pasa por el punto P y es perpendicular a la recta r.
  
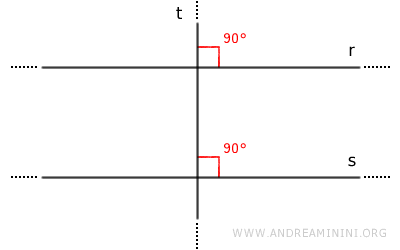
• Dos rectas r y s perpendiculares a una tercera recta t son paralelas entre sí
  Las rectas r y s forman pares de ángulos correspondientes congruentes. Por lo tanto, según el teorema de las rectas paralelas, son paralelas.
  
• Una recta t perpendicular a una recta r también es perpendicular a todas las rectas paralelas a r
  Dadas dos rectas paralelas r y s, si una recta t es perpendicular a una de ellas (r o s), también lo será a la otra.
  

  Demostración: Supongamos dos rectas paralelas r//s y una tercera recta t perpendicular a la recta s. Entonces, las rectas t y s forman un ángulo recto (α=90°).
  
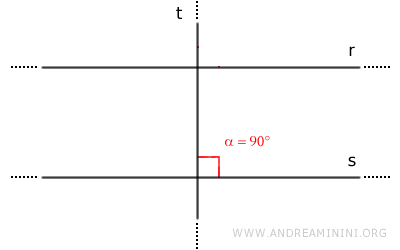
  Como r y s son paralelas (r//s), según el teorema de las rectas paralelas, las rectas r y s forman pares de ángulos correspondientes congruentes con la misma transversal (α≅β). Por lo tanto, el ángulo β también es recto (β=90°).
  
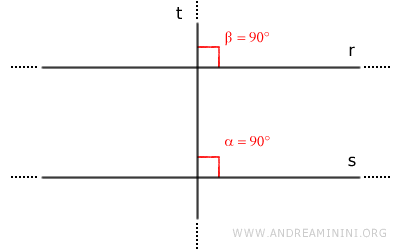
  En consecuencia, la recta t también es perpendicular a la recta r.

• Las perpendiculares a dos rectas secantes también son secantes entre sí
  Dadas dos rectas secantes r y s, sus respectivas perpendiculares p y q también se cortan.
  

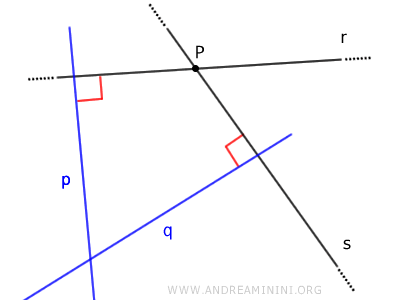
  Demostración: Esta afirmación se demuestra por reducción al absurdo. Supongamos que tenemos dos rectas secantes r y s, cuyas perpendiculares respectivas p y q fueran paralelas entre sí, es decir, p // q. Si p y q fueran paralelas, según el teorema de las rectas paralelas, los ángulos interiores alternos α y β respecto a una transversal t deberían sumar 180°.
  
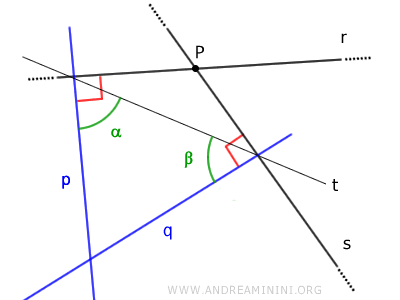
  Sin embargo, los ángulos α y β son ambos agudos, ya que corresponden a la división de un ángulo recto (90°). Por lo tanto, su suma es menor de 180°, lo que implica que p y q no pueden ser paralelas. Esto contradice la hipótesis inicial. En consecuencia, es falso que las perpendiculares p y q a dos rectas secantes r y s sean paralelas. Por lo tanto, la negación es verdadera: las perpendiculares a dos rectas secantes también son secantes entre sí, ya que la suma de los ángulos conjugados α + β es menor que 180°.

Y así sucesivamente.