Haz de rectas paralelas

Un haz de rectas paralelas es el conjunto de todas las rectas de un plano que son paralelas a una recta dada r.

Este tipo de haz está formado por infinitas rectas que mantienen la misma pendiente.

Suele representarse gráficamente mediante una sola recta de ejemplo, $ y = mx+q $, conocida como la recta base del haz.

Al modificar el término independiente $ q $, que representa la ordenada al origen, se obtienen todas las demás rectas paralelas a la base.

$$ y = mx+q $$

Otra forma de representar el haz es usando la ecuación implícita de la recta base:

$$ ax+by+k = 0 $$

En este caso, al variar el parámetro $ k $, se generan todas las rectas paralelas a la base.

Ejemplo. La ecuación $ y = 2x+q $ define una familia de rectas paralelas con pendiente constante $ m = 2 $. Si $ q = 0 $, la recta pasa por el origen: $ y = 2x $. Al cambiar el valor de $ q $, obtenemos las demás rectas del haz: por ejemplo, si $ q = 5 $, la ecuación es $ y = 2x + 5 $; si $ q = -5 $, entonces $ y = 2x - 5 $; si $ q = 10 $, $ y = 2x + 10 $, y así sucesivamente.

Ecuación implícita (cartesiana) del haz de rectas paralelas

La ecuación cartesiana (o forma implícita) de un haz de rectas paralelas se escribe así:

$$ ax + by + c = 0 $$

Los coeficientes $ a $ y $ b $ son constantes distintas de cero y determinan la dirección común de todas las rectas del haz.

El término independiente $ c $ funciona como parámetro variable que permite generar todas las rectas de la familia. 

En otras palabras, cada recta del haz se caracteriza por un valor concreto del término $ c $, que determina su posición relativa dentro del conjunto.

En el caso particular en que $ c = 0 $, la recta pasa por el origen de coordenadas, es decir, por el punto (0,0).

Nota. La recta principal r, que actúa como "base" del haz, también corresponde a un valor específico y único de $ c $. Por ejemplo, si la ecuación de la base es $ 2x + 3y - 5 = 0 $, entonces $ c = -5 $.

Existen dos casos especiales que conviene destacar:

• $ x = k $
  Esta es la ecuación de un haz de rectas verticales, paralelas al eje y. Cada recta corta al eje x en un punto distinto definido por el valor de $ k $, pero todas son perpendiculares al eje x. Si $ x = 0 $, la recta coincide con el eje y. Ejemplos: x = -5, x = -2, x = 1, x = 3, etc.
  
• $ y = k $
  Esta ecuación representa un haz de rectas horizontales, paralelas al eje x. En este caso, cada recta corta al eje y en un valor distinto de $ k $, pero todas son paralelas entre sí y no tienen pendiente. Si $ y = 0 $, la recta coincide con el eje x. Otros ejemplos: y = 3, y = 1, y = -1, y = -2, etc.
  

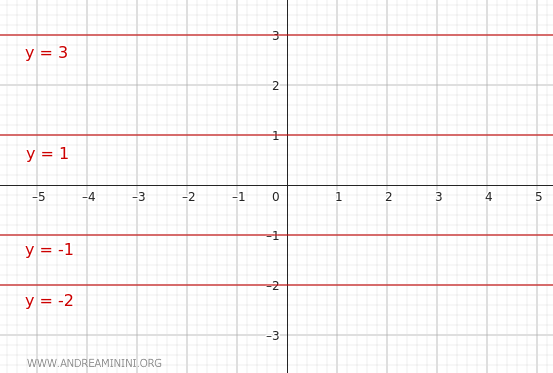
Estos dos casos resultan especialmente útiles para describir familias de rectas con dirección fija que se desplazan en paralelo respecto a uno de los ejes.

Ecuación del haz en forma explícita

También se puede expresar la ecuación del haz de rectas paralelas en forma explícita:

$$ y = mx + q $$

En esta expresión, cada valor de $ q $ define una recta distinta dentro del haz.

Cuando $ q = 0 $, la recta pasa por el origen.

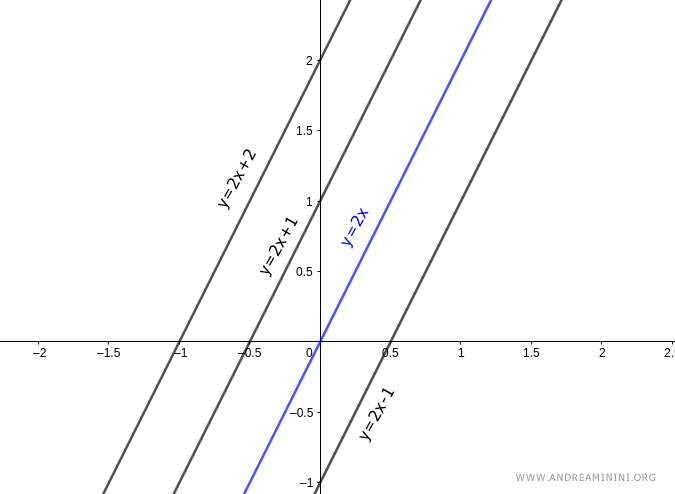
Nota. El valor de $ q $ representa la ordenada al origen, es decir, el punto donde la recta corta al eje y cuando $ x = 0 $.

Ecuación paramétrica

Otra forma útil de representar el haz es mediante la ecuación paramétrica:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$

Aquí, el punto $ (x_0, y_0) $ varía de una recta a otra, mientras que el vector de dirección $ (l, m) $ se mantiene constante.

Ejemplo

Dada la recta:

$$ 2x + 3y - 12 = 0 $$

Al modificar el valor de $ c $, se obtienen las rectas paralelas pertenecientes al haz.

 

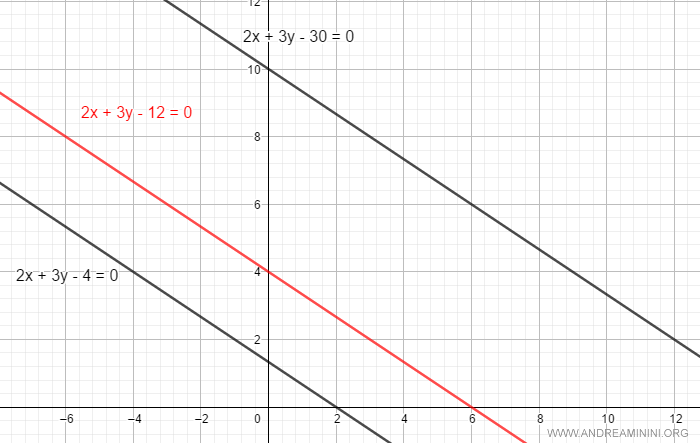
En forma paramétrica, esta recta se expresa así:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + t \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 1 \\ -\frac{2}{3} \end{pmatrix} $$

Al modificar el punto de paso (0,4) y conservar el vector de dirección, se generan todas las rectas del haz.

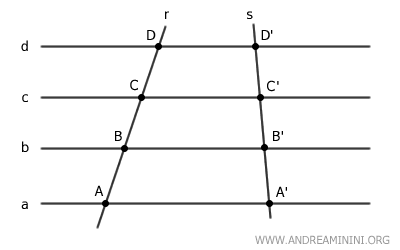
Transversal de un haz de rectas paralelas

Una transversal de un haz es una recta que corta a todas las rectas paralelas del haz.

Por ejemplo, la recta r es una transversal del haz.

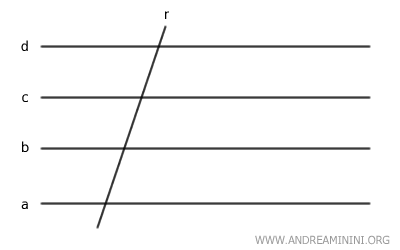
Cuando dos transversales diferentes cortan un haz de rectas paralelas, los puntos donde se cruzan con cada recta se llaman puntos correspondientes.

Por ejemplo, los puntos A y A' son puntos correspondientes.

Los segmentos cuyos extremos son puntos correspondientes sobre una misma transversal se llaman segmentos correspondientes.

Por ejemplo, los segmentos AB y BC son segmentos correspondientes.

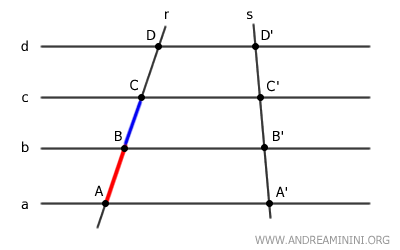
De igual manera, los segmentos A'B' y B'C' sobre la segunda transversal también son correspondientes.

Según el Teorema de Tales, cuando un haz de rectas paralelas es cortado por dos transversales, los segmentos correspondientes guardan una relación de proporcionalidad directa.

Por ejemplo, el segmento AB guarda la misma proporción con CD que A'B' con C'D'

$$ AB:CD = A'B':C'D' $$

Esta relación se conoce como la correspondencia de Tales.

Y así sucesivamente.