Distancia entre dos rectas alabeadas

La distancia entre dos rectas alabeadas $ r $ y $ s $ es la longitud del segmento perpendicular común $ AB $, que constituye el segmento más corto que une un punto de una recta con un punto de la otra. $$ AB \perp r $$ $$ AB \perp s $$ Aquí, $ A \in r $ y $ B \in s $.

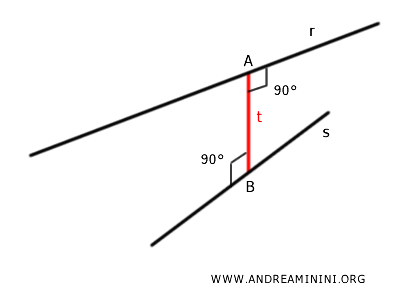
Existe una única recta $ t $ perpendicular a ambas rectas alabeadas $ r $ y $ s $.

Esta recta $ t $ corta a cada una de las rectas en un punto, $ A \in r $ y $ B \in s $, y el segmento $ AB $ que une estos puntos representa la menor distancia entre las dos rectas.

Por tanto, el segmento $ AB $ define la distancia entre las rectas alabeadas $ r $ y $ s $.

Nota. En el espacio tridimensional (x, y, z), dos rectas se denominan alabeadas si no se intersectan y no son paralelas.

Demostración
Ejemplo práctico

Demostración

Por definición, existe una única recta perpendicular a dos rectas alabeadas. Esta recta corta a cada una en un único punto, y el segmento que une dichos puntos es el de longitud mínima. Veamos cómo se demuestra esto.

Consideremos dos rectas alabeadas en el espacio tridimensional.

Como son alabeadas, dichas rectas ni se intersectan ni son paralelas.

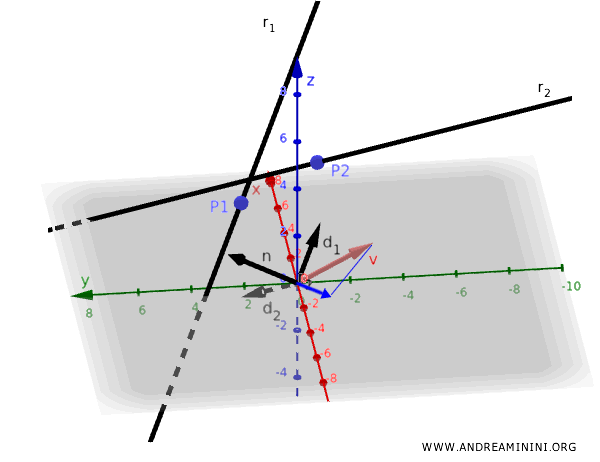
La primera recta $ r_1 $ pasa por el punto $ \mathbf{P}_1 $ y tiene como vector director $ \mathbf{d}_1 $.
La segunda recta $ r_2 $ pasa por el punto $ \mathbf{P}_2 $ y tiene como vector director $ \mathbf{d}_2 $.

Las ecuaciones paramétricas de las rectas son:

$$ r_1(t) = \mathbf{P}_1 + t \, \mathbf{d}_1 \quad \text{y} \quad r_2(s) = \mathbf{P}_2 + s \, \mathbf{d}_2 $$

donde $ t $ y $ s $ son parámetros reales.

Para encontrar una recta perpendicular a ambas $ r_1 $ y $ r_2 $, se deben cumplir dos condiciones:

La recta debe ser ortogonal al vector director $ \mathbf{d}_1 $ de $ r_1 $.
La recta debe ser también ortogonal al vector director $ \mathbf{d}_2 $ de $ r_2 $.

Un vector $ \mathbf{n} $ ortogonal a ambos se obtiene mediante el producto vectorial:

$$ \mathbf{n} = \mathbf{d}_1 \times \mathbf{d}_2 $$

Este vector $ \mathbf{n} $ sirve como vector director de la recta perpendicular buscada.

Consideremos ahora el vector $ \mathbf{v} $, que une un punto de $ r_1 $ con un punto de $ r_2 $:

$$ \mathbf{v} = \mathbf{P}_2 - \mathbf{P}_1 $$

La distancia mínima se obtiene proyectando $ \mathbf{v} $ sobre $ \mathbf{n} $:

$$ d = \frac{| \mathbf{v} \cdot \mathbf{n} |}{\|\mathbf{n}\|} $$

donde $ \mathbf{v} \cdot \mathbf{n} $ es el producto escalar de $ \mathbf{v} $ con $ \mathbf{n} $, y $ \|\mathbf{n}\| $ es la norma de $ \mathbf{n} $.

La recta perpendicular es única, ya que el vector $ \mathbf{n} $, obtenido como $ \mathbf{d}_1 \times \mathbf{d}_2 $, es único.

Por tanto, los puntos de intersección de esta recta con $ r_1 $ y $ r_2 $ están determinados de forma única, asegurando que el segmento mínimo también sea único.

Ejemplo práctico

Consideremos dos rectas alabeadas en el espacio, cuyas ecuaciones paramétricas son las siguientes:

La primera recta ($ r_1 $):

$$ r_1: \begin{cases}
x = 1 + t \\
y = 2 - t \\
z = 3 + 2t
\end{cases} $$

Aquí, $ \mathbf{P}_1 = (1, 2, 3) $ es un punto sobre $ r_1 $, y $ \mathbf{d}_1 = (1, -1, 2) $ es su vector director.

La segunda recta ($ r_2 $):

$$ r_2: \begin{cases}
x = 2 + s \\
y = -1 + 2s \\
z = 4 - s
\end{cases} $$

Aquí, $ \mathbf{P}_2 = (2, -1, 4) $ es un punto sobre $ r_2 $, y $ \mathbf{d}_2 = (1, 2, -1) $ es su vector director.

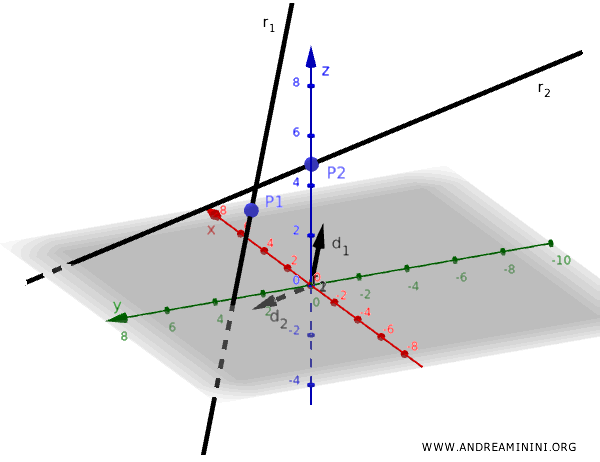
ejemplo de cálculo de distancia entre rectas alabeadas

Calculamos el vector $ \mathbf{n} $, ortogonal a los vectores directores $ \mathbf{d}_1 $ y $ \mathbf{d}_2 $, mediante el producto vectorial:

$$ \mathbf{n} = \mathbf{d}_1 \times \mathbf{d}_2 $$

Dados $ \mathbf{d}_1 = (1, -1, 2) $ y $ \mathbf{d}_2 = (1, 2, -1) $:

$$ \mathbf{n} = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
1 & -1 & 2 \\
1 & 2 & -1
\end{vmatrix}
= \mathbf{i} \begin{vmatrix} -1 & 2 \\ 2 & -1 \end{vmatrix}
- \mathbf{j} \begin{vmatrix} 1 & 2 \\ 1 & -1 \end{vmatrix}
+ \mathbf{k} \begin{vmatrix} 1 & -1 \\ 1 & 2 \end{vmatrix}
$$

$$ \mathbf{n} = \mathbf{i}(1 - 4) - \mathbf{j}(-1 - 2) + \mathbf{k}(2 + 1) $$

$$ \mathbf{n} = -3\mathbf{i} + 3\mathbf{j} + 3\mathbf{k} $$

Por tanto, el vector ortogonal a ambos vectores directores es:

$$ \mathbf{n} = (-3, 3, 3) $$

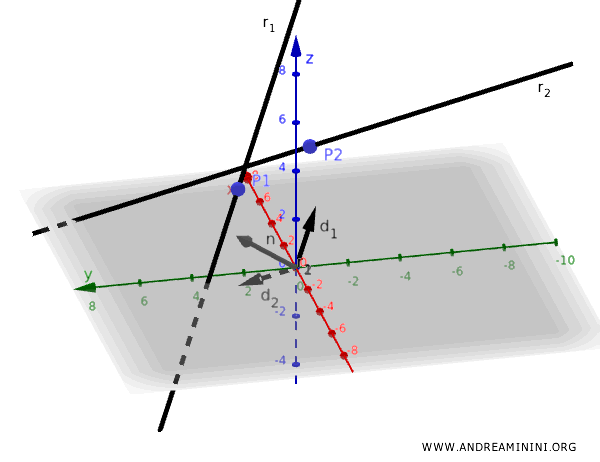
vector ortogonal calculado

Calculamos ahora el vector $ \mathbf{v} $ que une los puntos $ \mathbf{P}_1 = (1, 2, 3) $ y $ \mathbf{P}_2 = (2, -1, 4) $:

$$ \mathbf{v} = \mathbf{P}_2 - \mathbf{P}_1 = (2 - 1, -1 - 2, 4 - 3) = (1, -3, 1) $$

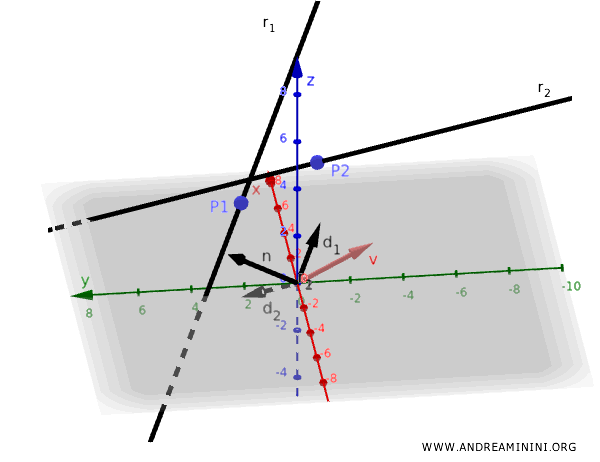
ejemplo de cálculo del vector unión entre puntos de las rectas

La distancia mínima entre las rectas es la proyección del vector $ \mathbf{v} $ sobre $ \mathbf{n} $:

proyección de un vector sobre otro para calcular la distancia

Calculamos la magnitud de dicha proyección mediante la fórmula:

$$ d = \frac{| \mathbf{v} \cdot \mathbf{n} |}{\|\mathbf{n}\|} $$

Primero, hallamos el producto escalar $ \mathbf{v} \cdot \mathbf{n} $:

$$ \mathbf{v} \cdot \mathbf{n} = (1)(-3) + (-3)(3) + (1)(3) = -3 - 9 + 3 = -9 $$

El valor absoluto es:

$$ | \mathbf{v} \cdot \mathbf{n} | = |-9| = 9 $$

Calculamos ahora la norma de $ \mathbf{n} $:

$$ \|\mathbf{n}\| = \sqrt{(-3)^2 + 3^2 + 3^2} = \sqrt{9 + 9 + 9} = \sqrt{27} = 3\sqrt{3} $$

Por último, la distancia es:

$$ d = \frac{9}{3\sqrt{3}} = \frac{3}{\sqrt{3}} = \sqrt{3} $$

Por tanto, la distancia mínima entre las dos rectas alabeadas es:

$$ d = \sqrt{3} $$

Esta distancia coincide con la longitud del segmento perpendicular común $ AB $ entre las dos rectas alabeadas.

segmento perpendicular común entre rectas alabeadas

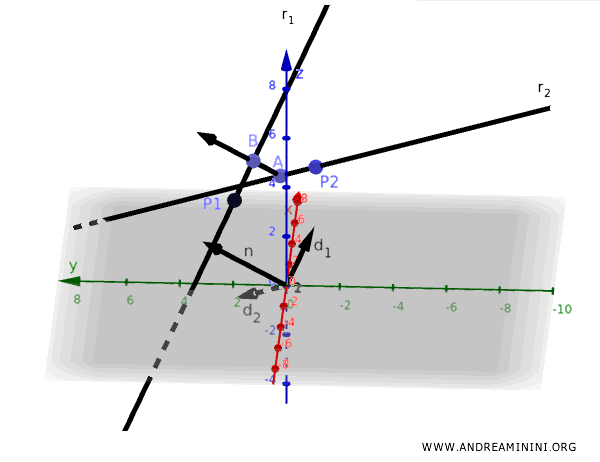
¡Y con esto, queda resuelto el ejemplo!