Cómo Determinar si Dos Rectas Son Secantes, Paralelas o Coincidentes

Para establecer la relación entre dos rectas en el plano cartesiano: $$ r: ax + by + c = 0 $$ y $$ r': a'x + b'y + c' = 0 $$ se analizan sus ecuaciones generales, comparando los coeficientes y los términos independientes.

• Rectas Secantes
  Si la proporción entre los coeficientes no es equivalente, las dos rectas se cortan en un único punto. $$ \frac{a}{a'} \ne \frac{b}{b'} $$
• Rectas Paralelas y Distintas
  Si la proporción entre los coeficientes es la misma, pero difiere de la proporción entre los términos independientes, las rectas son paralelas y distintas; es decir, nunca se cruzan. $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$
• Rectas Coincidentes
  Si la proporción entre los coeficientes es constante y coincide con la proporción entre los términos independientes, las rectas son coincidentes; es decir, se superponen en toda su extensión. $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$

Nota: Estas condiciones derivan directamente de los criterios de paralelismo $$ \frac{a}{a'} = \frac{b}{b'} $$ y de coincidencia de rectas $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$

Ejemplo Práctico

Consideremos las siguientes dos rectas:

$$ r: 2x + 3y + 4 = 0 $$

$$ r': 4x + 6y + 12 = 0 $$

Comprobemos primero si cumplen el criterio de paralelismo analizando la razón entre los coeficientes \( a = 2 \), \( b = 3 \) y \( a' = 4 \), \( b' = 6 \) de las ecuaciones.

$$ \frac{a}{a'} = \frac{2}{4} = \frac{1}{2} $$

$$ \frac{b}{b'} = \frac{3}{6} = \frac{1}{2} $$

La proporción entre los coeficientes es la misma, por lo que las rectas no se cortan.

$$ \frac{a}{a'} = \frac{b}{b'} = \frac{1}{2} $$

Esto indica que las rectas son paralelas, aunque aún debemos comprobar si son coincidentes o distintas.

Para ello, verificamos el criterio de coincidencia analizando la proporción entre los términos independientes \( c = 4 \) y \( c' = 12 \).

$$ \frac{c}{c'} = \frac{4}{12} = \frac{1}{3} $$

La proporción entre los términos independientes no coincide con la proporción de los coeficientes, por lo que las rectas no son coincidentes.

$$ \frac{c}{c'} = \frac{1}{3} \ne \frac{1}{2} = \frac{a}{a'} = \frac{b}{b'} $$

Por lo tanto, las dos rectas son paralelas pero distintas.

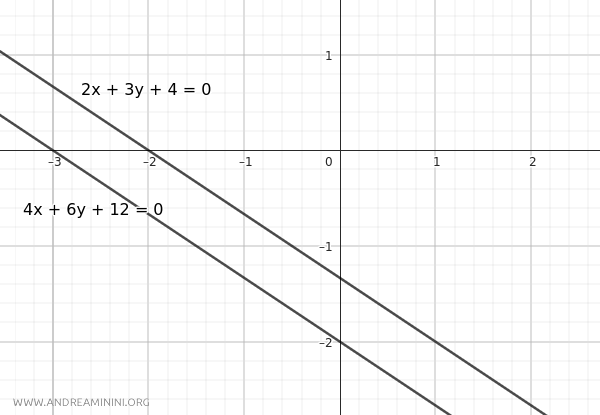
Ejemplo 2

En este ejemplo, consideremos las rectas:

$$ r: 2x + 3y + 4 = 0 $$

$$ r': 4x - 6y + 8 = 0 $$

Para determinar si se cortan o son paralelas, comprobamos si cumplen el criterio de paralelismo.

$$ \frac{a}{a'} = \frac{2}{4} = \frac{1}{2} $$

$$ \frac{b}{b'} = \frac{3}{-6} = -\frac{1}{2} $$

En este caso, no se cumple el criterio de paralelismo $$ \frac{a}{a'} = \frac{b}{b'} $$.

$$ \frac{1}{2} \ne -\frac{1}{2} $$

Por tanto, las rectas son secantes, es decir, se intersectan en un único punto.

¿Cuál es el punto de intersección de estas rectas?

Para hallarlo, resolvemos el siguiente sistema de ecuaciones lineales:

$$ \begin{cases} 2x + 3y + 4 = 0 \\ 4x - 6y + 8 = 0 \end{cases} $$

Resolveremos el sistema mediante el método de sustitución, aunque cualquier otro método sería igualmente válido.

Por ejemplo, despejamos \( x \) en la primera ecuación y lo sustituimos en la segunda.

$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ 4x - 6y + 8 = 0 \end{cases} $$

$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ 4 \cdot \left( \frac{-4 - 3y}{2} \right) - 6y + 8 = 0 \end{cases} $$

$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ \frac{-16 - 12y}{2} - 6y + 8 = 0 \end{cases} $$

$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ \frac{-16 - 12y - 12y + 16}{2} = 0 \end{cases} $$

$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ \frac{-24y}{2} = 0 \end{cases} $$

$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ -12y = 0 \end{cases} $$

$$ \begin{cases} x = \frac{-4 - 3y}{2} \\ y = 0 \end{cases} $$

Una vez hallado \( y = 0 \) en la segunda ecuación, lo sustituimos en la primera.

$$ \begin{cases} x = \frac{-4 - 3 \cdot 0}{2} \\ y = 0 \end{cases} $$

$$ \begin{cases} x = \frac{-4}{2} \\ y = 0 \end{cases} $$

$$ \begin{cases} x = -2 \\ y = 0 \end{cases} $$

La solución del sistema es \( x = -2 \) y \( y = 0 \).

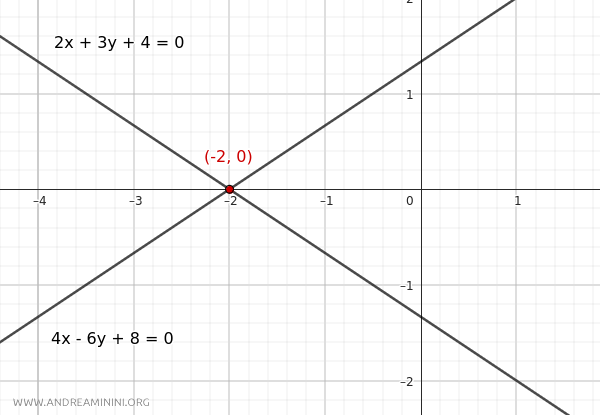
Por tanto, las rectas secantes se intersectan en el punto (x,y)=(-2,0) en el plano cartesiano.

Cálculo del Determinante

Un método alternativo, y a menudo más ágil, para determinar la relación entre dos rectas es calcular el determinante formado por los coeficientes de las variables \( x \) y \( y \).

$$ D = a \cdot b' - b \cdot a' $$

Donde \( a \), \( a' \), \( b \) y \( b' \) son los coeficientes de las variables \( x \) y \( y \) en las ecuaciones generales de las dos rectas.

$$ r: ax + by + c = 0 $$

$$ r': a'x + b'y + c' = 0 $$

En función del valor del determinante, las dos rectas pueden ser secantes o no cortarse en ningún punto:

• \( D \neq 0 \)
  Si el determinante es distinto de cero, las rectas se intersectan en un único punto.
• \( D = 0 \)
  Si el determinante es cero, las rectas no se cortan. En este caso, pueden ser paralelas y distintas o coincidentes.

Cuando el determinante es nulo \( D = 0 \), se cumple el criterio de paralelismo entre ambas rectas.

$$ \frac{a}{a'} = \frac{b}{b'} $$

Para saber si son coincidentes, es necesario comprobar si también satisfacen el criterio de coincidencia.

En ese caso, se calcula la razón entre los términos independientes y se verifica si \( \frac{c}{c'} \) coincide con \( \frac{a}{a'} \) y \( \frac{b}{b'} \).

• Si \( \frac{c}{c'} = \frac{a}{a'} = \frac{b}{b'} \), las rectas son coincidentes y comparten todos sus puntos.
• Si la razón \( \frac{c}{c'} \) es distinta, o alguna de las razones no existe (porque el denominador es cero mientras el numerador no lo es), entonces las rectas son paralelas y distintas.

Ejemplo

Consideremos las siguientes rectas:

$$ r: 2x + 3y + 4 = 0 $$

$$ r': 4x + 6y + 8 = 0 $$

Calculamos el determinante:

$$ D = 2 \times 6 - 3 \times 4 = 12 - 12 = 0 $$

Como \( D = 0 \), las rectas no se cortan, por lo que son paralelas.

Veamos ahora si son coincidentes o distintas.

$$ \frac{2}{4} = \frac{3}{6} = \frac{4}{8} = \frac{1}{2} $$

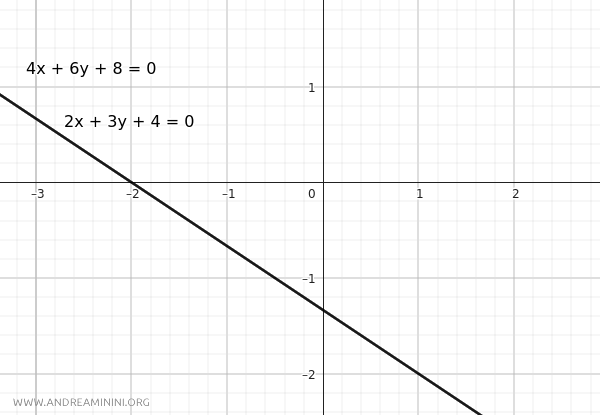
Las tres razones coinciden, por lo tanto, las rectas son coincidentes.

Gracias a este método, es posible analizar la relación entre dos rectas únicamente a partir de sus coeficientes y términos independientes, sin necesidad de resolver un sistema de ecuaciones lineales.

Y así sucesivamente.