Rectas Coplanarias, Cruzadas, Paralelas o Secantes en el Espacio

En el espacio, dos rectas pueden ser coplanarias o cruzadas, según estén contenidas o no en un mismo plano. Las rectas coplanarias, a su vez, se clasifican en paralelas (distintas o coincidentes) o secantes.

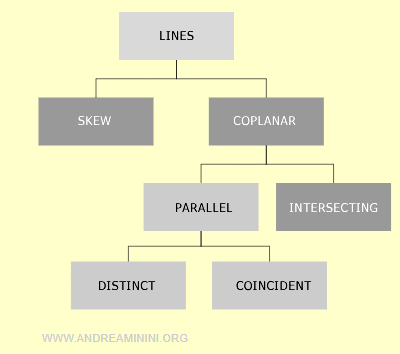
Posiciones Relativas de las Rectas en el Espacio

En el espacio tridimensional (x, y, z), las rectas pueden ser cruzadas o coplanarias, según su disposición espacial.

• Rectas Coplanarias
  Dos rectas son coplanarias si se encuentran en un mismo plano. Estas pueden ser secantes si se intersectan en un único punto, coincidentes si comparten todos sus puntos, o paralelas si no se cruzan en ningún punto.
  
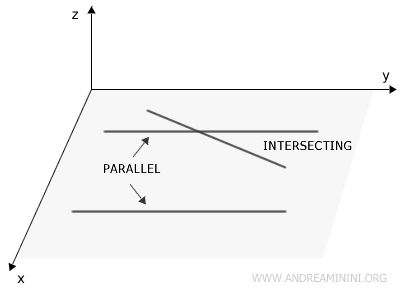
• Rectas Cruzadas
  Dos rectas son cruzadas si no están contenidas en el mismo plano. En este caso, pertenecen a planos distintos, no se cortan y tampoco son paralelas.
  

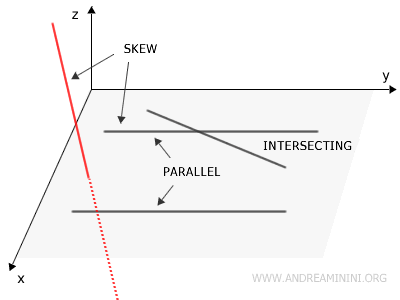
  La particularidad de las rectas cruzadas es que no existe ningún plano que pueda contenerlas simultáneamente. Por eso se diferencian de las rectas paralelas, que aunque no se intersectan, sí se hallan en un mismo plano. Para visualizar rectas cruzadas, piensa en dos lápices suspendidos en el aire, colocados de forma que no se toquen ni sean paralelos entre sí.

Cómo Determinar si Dos Rectas son Coplanarias

Para determinar si dos rectas son coplanarias, recurrimos al álgebra lineal.

El método varía según si las ecuaciones de las rectas están expresadas en forma cartesiana o vectorial/paramétrica.

A] Ecuaciones Cartesianas

En forma cartesiana, una recta puede representarse como la intersección de dos planos:

$$ \begin{cases} a_1 x + b_1 y + c_1 z + d_1 = 0 \\ a_2 x + b_2 y + c_2 z + d_2 = 0 \end{cases} $$

$$ \begin{cases} a_3 x + b_3 y + c_3 z + d_3 = 0 \\ a_4 x + b_4 y + c_4 z + d_4 = 0 \end{cases} $$

Podemos escribir las ecuaciones como un único sistema:

$$ \begin{cases} a_1 x + b_1 y + c_1 z + d_1 = 0 \\ a_2 x + b_2 y + c_2 z + d_2 = 0 \\ a_3 x + b_3 y + c_3 z + d_3 = 0 \\ a_4 x + b_4 y + c_4 z + d_4 = 0 \end{cases} $$

o, de forma equivalente:

$$ \begin{cases} a_1 x + b_1 y + c_1 z = - d_1 \\ a_2 x + b_2 y + c_2 z = - d_2 \\ a_3 x + b_3 y + c_3 z = - d_3 \\ a_4 x + b_4 y + c_4 z = - d_4 \end{cases} $$

Este sistema tiene tres incógnitas (x, y, z).

La matriz de coeficientes es:

$$ A = \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \\ a_4 & b_4 & c_4 \end{pmatrix} $$

La matriz ampliada es:

$$ A|B = \begin{pmatrix} a_1 & b_1 & c_1 & -d_1 \\ a_2 & b_2 & c_2 & -d_2 \\ a_3 & b_3 & c_3 & -d_3 \\ a_4 & b_4 & c_4 & -d_4 \end{pmatrix} $$

Según el teorema de Rouché-Capelli, el sistema es compatible (tiene solución) si el rango de A coincide con el rango de A|B. En ese caso, las rectas son coplanarias, ya sea secantes o coincidentes.

• Si el rango (r) es igual al número de incógnitas (n = 3), el sistema tiene una única solución, lo que indica que las rectas se cruzan en un punto.
  $$ rg(A) = rg(A|B) = 3 $$
• Si el rango (r) es menor que el número de incógnitas (n = 3), el sistema tiene infinitas soluciones (∞^n-r), lo que implica que las rectas son coincidentes.
  $$ rg(A) = rg(A|B) < 3 $$

Si el rango de A es distinto al de A|B, el sistema es incompatible, y las rectas pueden ser cruzadas o paralelas coplanarias.

• Si el rango (r) de A|B es igual a 4, los vectores de dirección de las rectas son linealmente independientes y las rectas son cruzadas.
  $$ rg(A) \ne rg(A|B) = 4 $$
• Si el rango (r) de A|B es menor que 4, los vectores de dirección son linealmente dependientes, y las rectas son paralelas y coplanarias.
  $$ rg(A) \ne rg(A|B) < 4 $$

Ejemplo

Consideremos las siguientes ecuaciones cartesianas de dos rectas en el espacio:

$$ \begin{cases} 4x+3y+2z=4 \\ -3x+2y+z=4 \end{cases} $$

$$ \begin{cases} 3x-4y-2z=2 \\ -3x-3y+2z=1 \end{cases} $$

Las combinamos en un solo sistema lineal:

$$ \begin{cases} 4x+3y+2z=4 \\ -3x+2y+z=4 \\ 3x-4y-2z=2 \\ -3x-3y+2z=1 \end{cases} $$

Calculamos el rango de la matriz de coeficientes A:

$$ r_A = \begin{pmatrix} 4 & 3 & 2 \\ -3 & 2 & 1 \\ 3 & -4 & -2 \\ -3 & -3 & 2 \end{pmatrix} = 3 $$

y el rango de la matriz ampliada A|B:

$$ r_{A|B} = \begin{pmatrix} 4 & 3 & 2 & 4 \\ -3 & 2 & 1 & 4 \\ 3 & -4 & -2 & 2 \\ -3 & -3 & 2 & 1 \end{pmatrix} = 4 $$

Como los rangos no coinciden, el sistema es incompatible.

Por tanto, las dos rectas son cruzadas, ya que el rango de A|B es 4.

B] Ecuaciones Vectoriales o Paramétricas

Si las rectas están dadas en forma vectorial o paramétrica, debemos comprobar si sus vectores de dirección son linealmente dependientes o independientes.

$$ \begin{cases} x = x_1 + l_1 t_1 \\ y = y_1 + m_1 t_1 \\ z = z_1 + n_1 t_1 \end{cases} $$

$$ \begin{cases} x = x_2 + l_2 t_2 \\ y = y_2 + m_2 t_2 \\ z = z_2 + n_2 t_2 \end{cases} $$

Construimos una matriz con los vectores de dirección:

$$ r_k = \begin{pmatrix} l_1 & l_2 \\ m_1 & m_2 \\ n_1 & n_2 \end{pmatrix} $$

Si el rango es:

• r_k = 1. Los vectores de dirección son linealmente dependientes. Entonces, las rectas son paralelas y distintas o coincidentes, pero siempre coplanarias.
  • Si tienen infinitos puntos en común, son coincidentes.
  • Si no tienen ningún punto en común, son paralelas.
• r_k = 2. Los vectores de dirección son linealmente independientes. En este caso, las rectas pueden ser coplanarias y secantes o bien cruzadas.
  • Si comparten un punto, son coplanarias y secantes.
  • Si no comparten ningún punto, son cruzadas.

Ejemplo

Consideremos las siguientes ecuaciones paramétricas de dos rectas en el espacio:

$$ \begin{cases} x = 3 + 2t_1 \\ y = -1 + 3t_1 \\ z = 1 + 4t_1 \end{cases} $$

$$ \begin{cases} x = 1 + 3t_2 \\ y = 2 + t_2 \\ z = 4 - 2t_2 \end{cases} $$

Los vectores de dirección de ambas rectas son:

$$ v_1 = \begin{pmatrix} 2 \\ 3 \\ 4 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} 3 \\ 1 \\ -2 \end{pmatrix} $$

Formamos la matriz con estos vectores como columnas:

$$ \begin{pmatrix} 2 & 3 \\ 3 & 1 \\ 4 & -2 \end{pmatrix} $$

Calculamos su rango:

$$ r_k = \begin{pmatrix} 2 & 3 \\ 3 & 1 \\ 4 & -2 \end{pmatrix} = 2 $$

El rango es 2.

Por tanto, los vectores son linealmente independientes.

En este punto, las rectas podrían ser cruzadas o coplanarias y secantes.

Verificamos si tienen puntos en común resolviendo el sistema:

$$ \begin{cases} x = 3 + 2t_1 \\ y = -1 + 3t_1 \\ z = 1 + 4t_1 \\ x = 1 + 3t_2 \\ y = 2 + t_2 \\ z = 4 - 2t_2 \end{cases} $$

$$ \begin{cases} 1 + 3t_2 = 3 + 2t_1 \\ 2 + t_2 = -1 + 3t_1 \\ 4 - 2t_2 = 1 + 4t_1 \end{cases} $$

$$ \begin{cases} t_2 = \frac{2 + 2t_1}{3} \\ 2 + \frac{2 + 2t_1}{3} = -1 + 3t_1 \\ 4 - 2t_2 = 1 + 4t_1 \end{cases} $$

$$ \begin{cases} t_2 = \frac{2 + 2t_1}{3} \\ t_1 = \frac{11}{7} \\ 4 - 2t_2 = 1 + 4t_1 \end{cases} $$

$$ \begin{cases} t_2 = \frac{2 + 2(\frac{11}{7})}{3} \\ t_1 = \frac{11}{7} \\ \frac{4}{7} = \frac{51}{7} \end{cases} $$

El sistema resulta incompatible. Las rectas no tienen puntos en común.

Por tanto, las rectas son cruzadas.

Y así sucesivamente.