Rectas Cruzadas
Las rectas cruzadas (alabeadas) son dos rectas en el espacio tridimensional (x, y, z) que no se encuentran en un mismo plano, no son paralelas y tampoco se cortan.
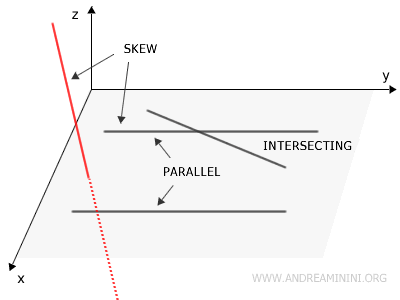
En otras palabras, no existe ningún plano único que pueda contener simultáneamente a ambas rectas cruzadas.
Esto implica que las rectas cruzadas no comparten ningún punto, aunque puedan intersectar el mismo plano, y que tampoco son paralelas entre sí.
El concepto de rectas cruzadas es exclusivo de la geometría tridimensional (x, y, z), ya que en un espacio bidimensional (x, y), todas las rectas se hallan necesariamente en el mismo plano y, por lo tanto, o se cortan o son paralelas. A diferencia de las rectas en el plano, que siempre se intersecan o son paralelas, las rectas cruzadas jamás se encuentran.
Un Ejemplo Práctico
Consideremos un sólido en el espacio tridimensional.
Por ejemplo, un cubo.
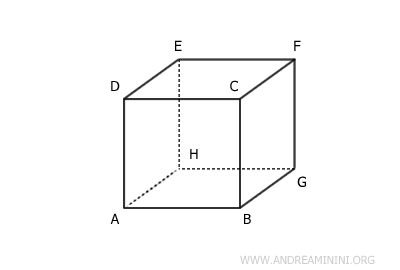
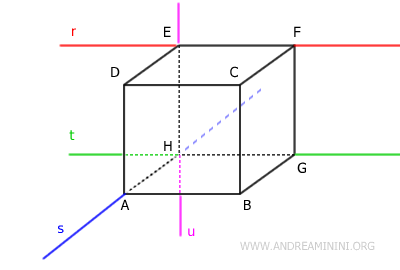
Imaginemos ahora una recta r (roja) que pasa por los vértices E y F del cubo, y una recta s (azul) que pasa por los vértices A y H.
Las rectas r y s, situadas respectivamente sobre las aristas EF y AH, son rectas cruzadas, pues no están contenidas en el mismo plano, no se cruzan y no son paralelas.
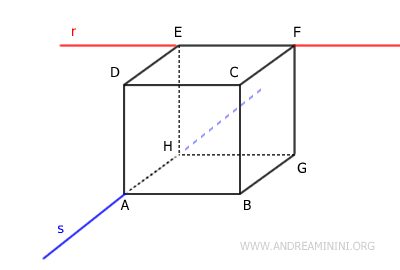
Por el contrario, las rectas r (roja) y t (verde) no son cruzadas, ya que, aunque no se intersecan ni se hallan en el mismo plano, sí son paralelas entre sí.
Tampoco son cruzadas las rectas r (roja) y p (morada), porque se cortan en el punto E.
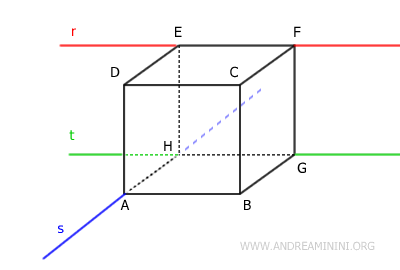
Del mismo modo, las rectas s (azul) y t (verde) no son cruzadas, pues se intersecan en el punto H y se encuentran en un mismo plano.
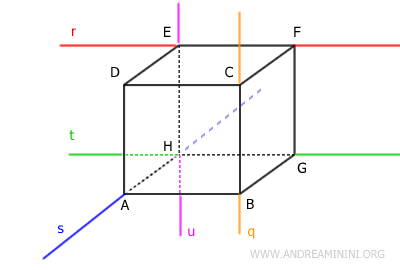
Por último, las rectas s (azul) y q (amarilla) sí son rectas cruzadas, ya que no se cruzan ni son paralelas.
Por la misma razón, también son cruzadas las rectas r (roja) y q (amarilla), así como las rectas t (verde) y q (amarilla).
En cambio, las rectas u (morada) y q (amarilla) no son cruzadas porque son paralelas y pueden situarse en un mismo plano.
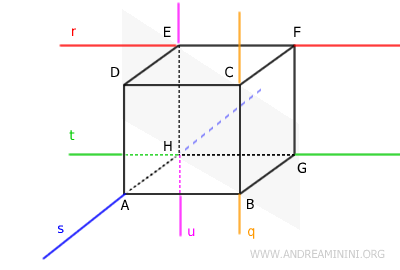
De estos ejemplos se desprenden las principales características de las rectas cruzadas: no deben cruzarse y no pueden ser paralelas.
Nota: Estas dos condiciones (no intersección y no paralelismo) son suficientes para definir rectas cruzadas, ya que implican, de forma indirecta, que ambas rectas no están contenidas en un mismo plano.
Características de las Rectas Cruzadas
Dos rectas son cruzadas si cumplen las siguientes condiciones:
- No se intersecan
Las rectas cruzadas jamás se cruzan. Es decir, no tienen ningún punto en común. - No son paralelas
Aunque no se crucen, tampoco mantienen entre sí una dirección paralela.
Dicho de otro modo, las rectas cruzadas se caracterizan por no intersectarse y no ser paralelas.
Esto implica que no se encuentran contenidas en un mismo plano. De hecho, en un plano, dos rectas solo pueden ser paralelas o secantes.
Sin embargo, esto no significa que dos rectas cruzadas no puedan tener puntos situados en un mismo plano, siempre que se trate de puntos distintos.
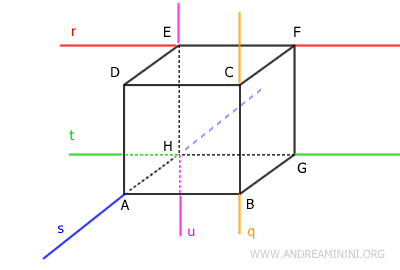
Por ejemplo, las rectas r (azul) y q (amarilla) son cruzadas aunque tengan los puntos A y B contenidos en el mismo plano. No obstante, dichos puntos no coinciden.
¿Por Qué las Rectas Cruzadas No Pueden Intersecarse?
Las rectas cruzadas no pueden compartir un punto, ya que, por definición, se encuentran en planos distintos.
Para demostrarlo, supongamos, por absurdo, que dos rectas cruzadas, r1 y r2, se cruzan en un punto \( P \).
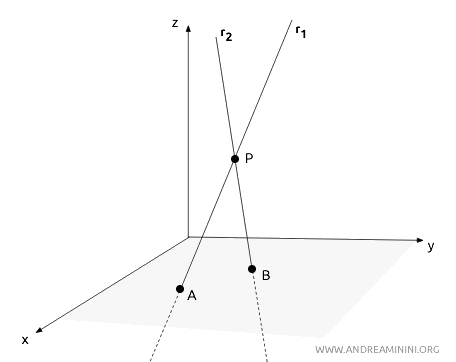
Si así fuera, podríamos elegir un punto \( A \) en una de las rectas y un punto \( B \) en la otra, distintos de \( P \).
Los tres puntos \( P \), \( A \) y \( B \) definirían un único plano β que contendría ambas rectas, convirtiéndolas en coplanarias.
Esto contradiría la propia definición de rectas cruzadas, que por naturaleza son no coplanarias.
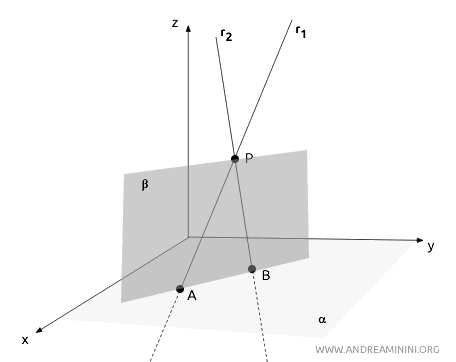
Por tanto, si dos rectas comparten un punto, necesariamente están en un mismo plano y, en consecuencia, no pueden ser cruzadas.
En conclusión, las rectas cruzadas y las rectas secantes son conceptos mutuamente excluyentes: si dos rectas son coplanarias, no pueden ser cruzadas; y si son cruzadas, no pueden cruzarse.
Y así sucesivamente.