Ecuación Polar de una Recta

La ecuación de una recta en forma polar puede expresarse de la siguiente manera:


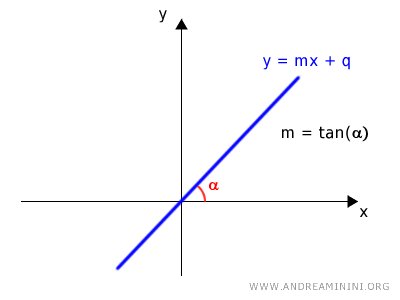
• Si la recta pasa por el origen, basta conocer el ángulo α, que determina la pendiente (m) de la recta y = mx + q, donde $$ m = \tan \alpha, \quad \text{con} \quad \alpha \ne \frac{\pi}{2} + k\pi $$ y q = 0.
  
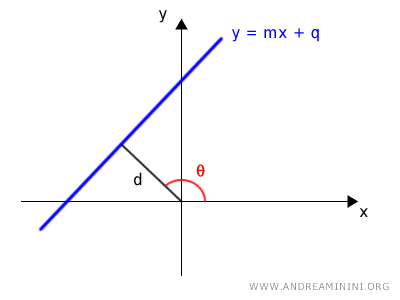
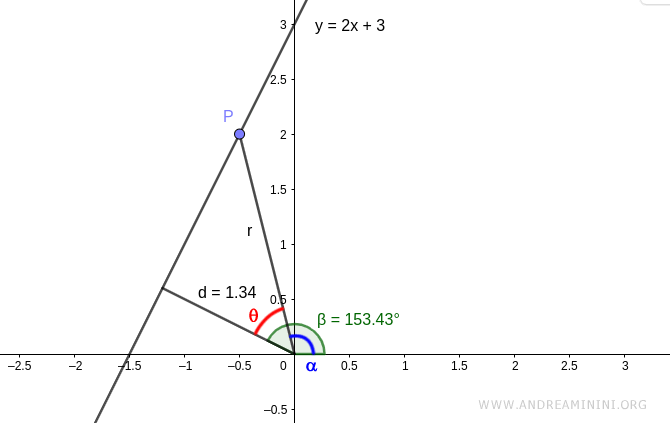
• Si la recta no pasa por el origen, es necesario conocer la distancia d entre la recta y el polo (origen), así como el ángulo β que forma el segmento d con el eje polar positivo: $$ d = r \cdot \cos(\beta - \alpha) $$

  
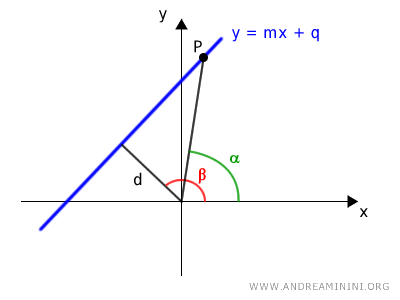
  Aquí, α es el ángulo en coordenadas polares de un punto P cualquiera sobre la recta.
  
  La diferencia θ = β - α es el ángulo interior entre ambos segmentos.
  

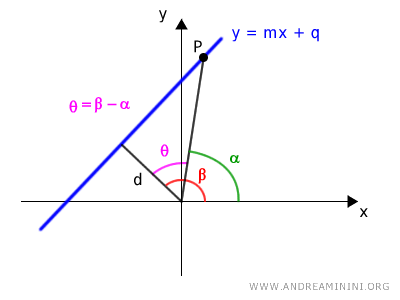
Naturalmente, si la recta pasa por el origen, la distancia d es cero.

Ejemplo Práctico

Ejemplo 1: Conversión de Forma Cartesiana a Polar

Consideremos la recta:

$$ y = 2x + 3 $$

Queremos hallar sus coordenadas polares.

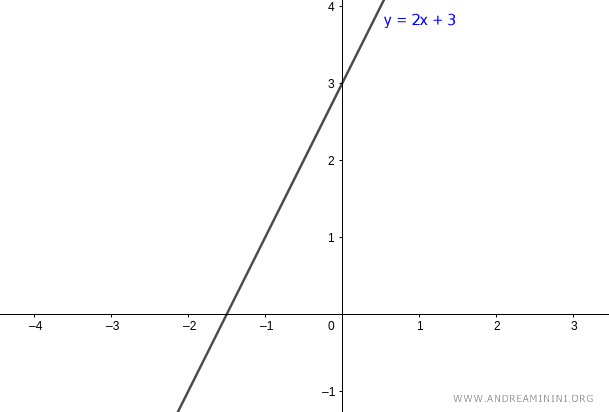
La pendiente de la recta es m = 2:

$$ m = 2 $$

Por tanto, el ángulo que forma la recta con el eje polar es:

$$ m = \tan \alpha $$

Aplicando la arco tangente en ambos lados, obtenemos:

$$ \arctan(m) = \arctan(\tan \alpha) $$

$$ \arctan(m) = \alpha $$

Como m = 2:

$$ \alpha = \arctan(2) $$

$$ \alpha = 63.43^\circ $$

Así, el ángulo entre la recta y el eje polar es α = 63.43°.

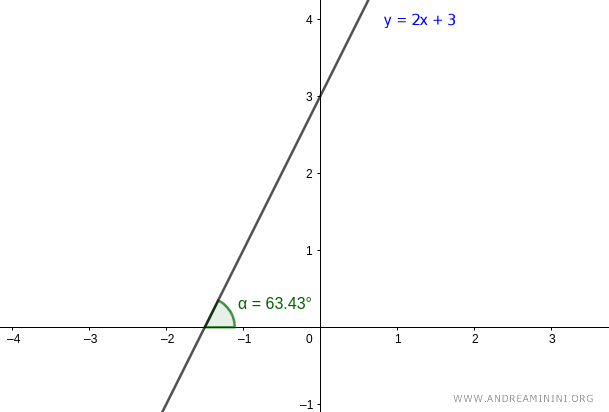
Ya tenemos uno de los parámetros de la ecuación polar de la recta.

Ahora necesitamos calcular el otro parámetro: la distancia d entre la recta y el polo (origen).

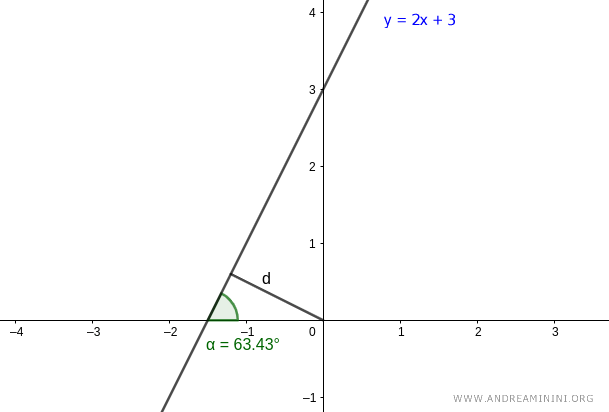
Elegimos un punto P sobre la recta.

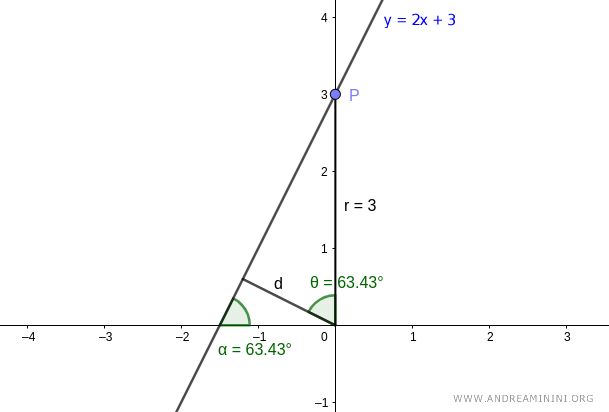
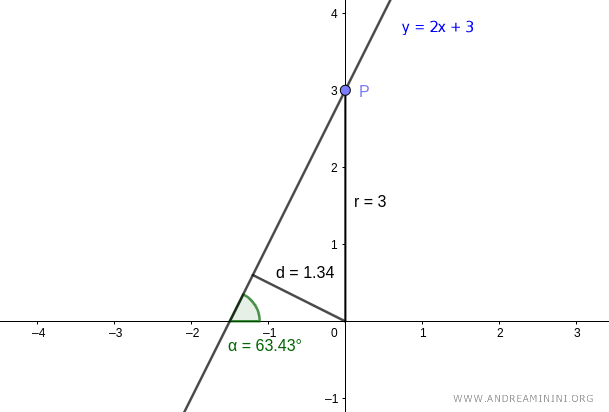
Para simplificar, tomamos el punto P en las coordenadas (0, 3), cuyo radio vector es r = 3. En este caso, el ángulo θ entre los dos segmentos coincide con α, es decir, θ = α = 63.43°.

Nota. Cualquier otro punto P de la recta serviría igualmente.

Como conocemos θ = 63.43° y r = 3, podemos calcular la distancia d:

$$ d = r \cdot \cos(\theta) $$

$$ d = 3 \cdot \cos(63.43^\circ) $$

$$ d = 1.34 $$

Así hallamos la distancia mínima (d) entre la recta y el polo.

Por tanto, las coordenadas polares de la recta son [63.43°, 1.34].

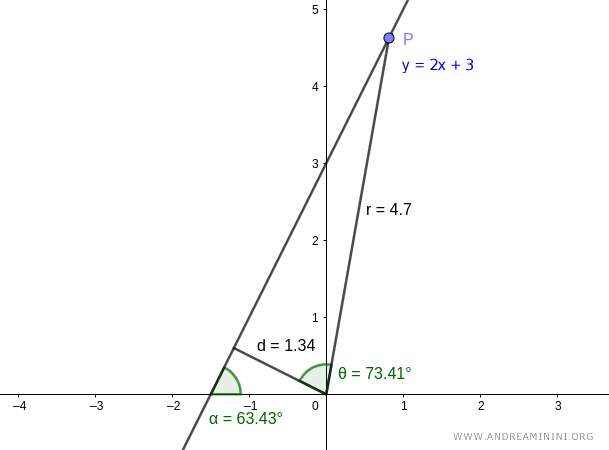
Nota. Como se indicó, cualquier otro punto P sobre la recta habría conducido al mismo resultado. Por ejemplo, eligiendo otro punto P con coordenadas distintas se obtendría un ángulo interno θ = 73.41° y una longitud r = 4.7, pero la distancia sería igualmente d = 4.7 · cos(73.41°) = 1.34.

Ejemplo 2: Conversión de Forma Polar a Cartesiana

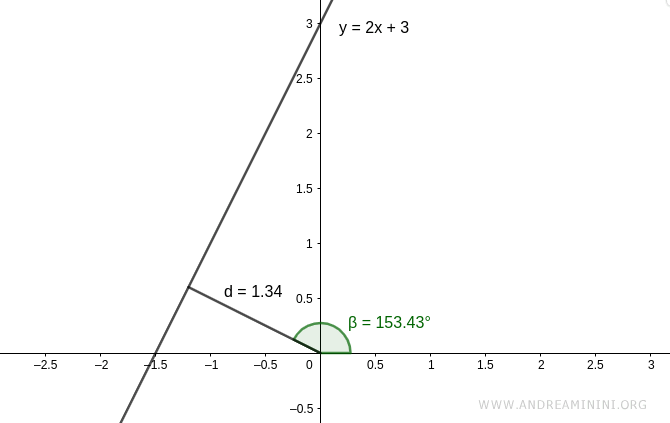
Consideremos ahora una recta definida en forma polar:

$$ d = 1.34 $$

$$ \beta = 153.43^\circ $$

Queremos deducir su ecuación cartesiana y = mx + q a partir de estos datos.

Tomemos las coordenadas polares [α, r] de un punto genérico P sobre la recta.

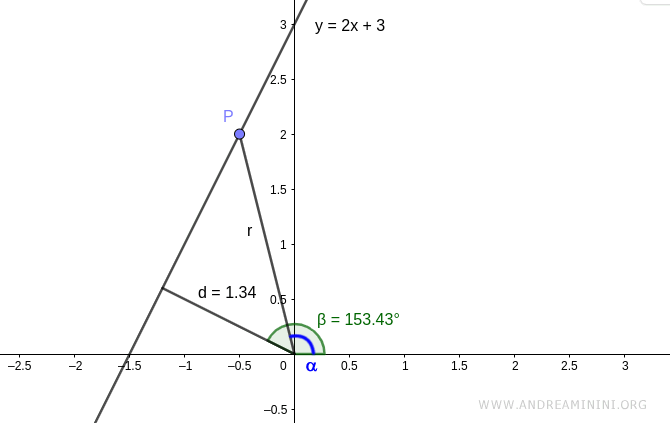
Sabemos que la distancia d de la recta al polo (origen) se calcula así:

$$ d = r \cdot \cos(\theta) $$

donde θ es el ángulo interno entre los segmentos d y r, y se obtiene como diferencia de ángulos: θ = β - α.

Por lo tanto, podemos escribir:

$$ d = r \cdot \cos(\beta - \alpha) $$

Sustituyendo β = 153.43°:

$$ d = r \cdot \cos(153.43^\circ - \alpha) $$

Y dado que d = 1.34:

$$ 1.34 = r \cdot \cos(153.43^\circ - \alpha) $$

Aplicamos la fórmula del coseno de la diferencia: cos(β - α) = cos(β)·cos(α) + sin(β)·sin(α):

$$ 1.34 = r \cdot [ \cos(153.43^\circ) \cos(\alpha) + \sin(153.43^\circ) \sin(\alpha) ] $$

$$ 1.34 = r \cdot \cos(153.43^\circ) \cos(\alpha) + r \cdot \sin(153.43^\circ) \sin(\alpha) $$

Dado que x = r · cos(α):

$$ 1.34 = [ r \cdot \cos(\alpha) ] \cdot \cos(153.43^\circ) + r \cdot \sin(153.43^\circ) \sin(\alpha) $$

$$ 1.34 = x \cdot \cos(153.43^\circ) + r \cdot \sin(153.43^\circ) \sin(\alpha) $$

Y que y = r · sin(α):

$$ 1.34 = x \cdot \cos(153.43^\circ) + y \cdot \sin(153.43^\circ) $$

Despejando y:

$$ y = \frac{ 1.34 }{ \sin(153.43^\circ) } - x \cdot \frac{ \cos(153.43^\circ) }{ \sin(153.43^\circ) } $$

La razón cos(153.43°)/sin(153.43°) equivale a -2:

$$ y = \frac{ 1.34 }{ \sin(153.43^\circ) } - x \cdot (-2) $$

$$ y = \frac{ 1.34 }{ \sin(153.43^\circ) } + 2x $$

La razón 1.34 / sin(153.43°) resulta ser igual a 3:

$$ y = 3 + 2x $$

Así obtenemos la ecuación cartesiana de la recta.

Demostración

1) Recta que Pasa por el Origen

Para una recta que pasa por el origen, se cumple que q = 0:

$$ y = m \cdot x $$

Gráficamente:

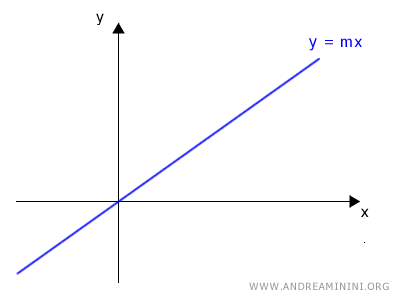
Tomemos un punto cualquiera P sobre la recta.

Este punto P tiene coordenadas cartesianas (x, y).

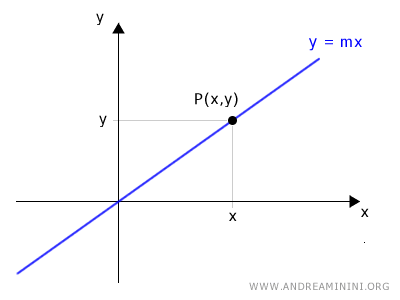
Trazamos un segmento que une el origen O con el punto P.

El segmento OP tiene longitud r y forma un ángulo α con respecto al eje x.

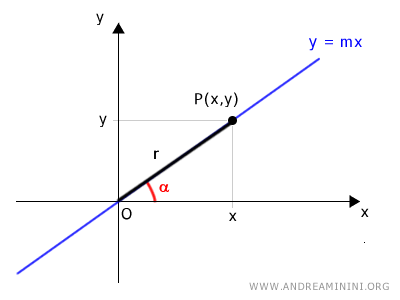
Conociendo el ángulo α y la longitud del segmento OP, podemos expresar las coordenadas cartesianas (x, y) del punto P en función de las funciones seno y coseno.

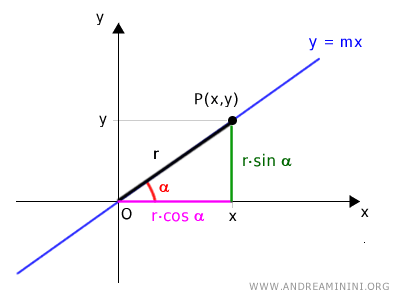
Así, las coordenadas polares del punto P son [r, α]:

$$ y = r \cdot \sin \alpha $$ $$ x = r \cdot \cos \alpha $$

Sustituyendo x e y en forma trigonométrica en la ecuación de la recta:

$$ y = m \cdot x $$

$$ r \cdot \sin \alpha = m \cdot (r \cdot \cos \alpha) $$

Simplificamos dividiendo ambos lados por r:

$$ \sin \alpha = m \cdot \cos \alpha $$

Podemos ahora despejar la pendiente m de la recta:

$$ m = \frac{\sin \alpha}{\cos \alpha} $$

De acuerdo con el segundo principio de la trigonometría, se cumple que tan α = sin α/cos α

Por tanto, podemos sustituir el cociente seno/coseno por la tangente:

$$ m = \tan \alpha $$

La tangente está indefinida en 90° (π/2) y sus múltiplos, es decir, en los ángulos 90° ± k·180° o π/2 ± k·π:

$$ m = \tan \alpha \quad \text{con} \quad \alpha \ne \frac{\pi}{2} + k \pi $$

donde k es un número entero.

Esto concluye la demostración de la ecuación polar para una recta que pasa por el origen.

2) Ecuación de una Recta que No Pasa por el Origen

Consideremos ahora una recta que pasa por un punto P en el plano, pero que no atraviesa el origen.

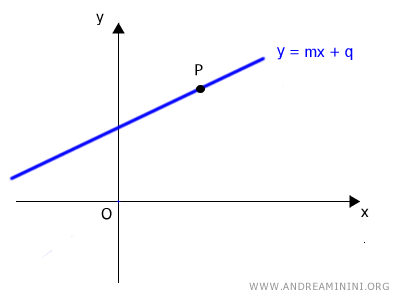
Cualquier recta que no pase por el origen puede quedar definida de manera única mediante dos parámetros polares:

• la distancia (d) entre la recta y el polo (origen)
• el ángulo β que forma el segmento de distancia con el eje polar

La distancia mínima entre la recta y el polo es el segmento OA, que parte del origen y es perpendicular a la recta.

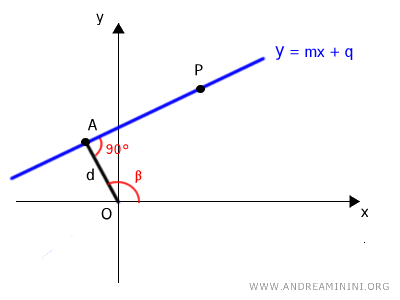
El segmento OA forma un ángulo β con el eje polar positivo y tiene longitud d, que debemos calcular.

Para determinar esta distancia d, trazamos el segmento OP que une el polo con el punto P sobre la recta.

El segmento OP forma un ángulo α con el eje polar.

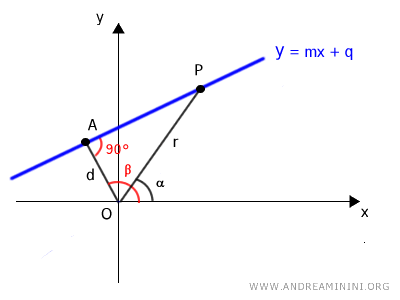
Esto genera un triángulo rectángulo OAP.

Así podemos aplicar los teoremas de los triángulos rectángulos.

Según el primer teorema de los triángulos rectángulos, la longitud de un cateto (OA) es igual al producto de la hipotenusa (OP) por el coseno del ángulo agudo θ = AOP:

$$ \overline{OA} = \overline{OP} \cdot \cos \widehat{AOP} $$

donde el ángulo θ = AOP es el ángulo agudo adyacente al cateto OA.

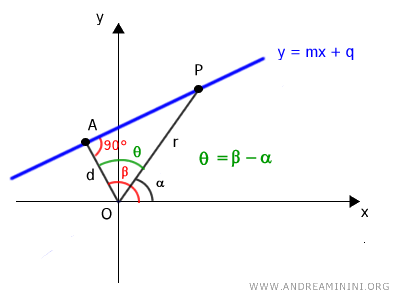
El ángulo θ = OAP también puede expresarse como la diferencia entre los ángulos beta y alpha: θ = \beta - \alpha

$$ \overline{OA} = \overline{OP} \cdot \cos(\beta - \alpha) $$

Sabiendo que OA es la distancia d entre la recta y el polo, y que OP es la longitud r:

$$ d = r \cdot \cos(\beta - \alpha) $$

Así obtenemos la fórmula de la distancia que queríamos demostrar.

Y así sucesivamente.