Ecuación de la Recta que Pasa por un Punto con Pendiente Dada
La ecuación de una recta que pasa por un punto concreto P(x1, y1) y tiene una pendiente m se expresa de la siguiente forma: $$ y = m \cdot (x - x_1) + y_1 $$ donde (x, y) representan cualquier otro punto situado sobre la recta.
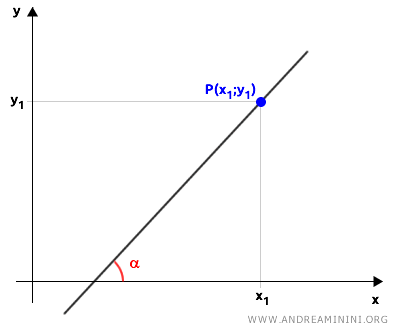
Esta fórmula nos permite determinar la ecuación de una recta conociendo únicamente un punto (x1, y1) y su pendiente.
La pendiente de una recta indica su inclinación respecto al eje x y se calcula como:
$$ m = \frac{y - y_1}{x - x_1} $$
Es decir, es el cociente entre la diferencia de las ordenadas $ (y - y_1) $ y la diferencia de las abscisas $ (x - x_1) $, lo que cuantifica cuán inclinada está la recta respecto al eje horizontal.
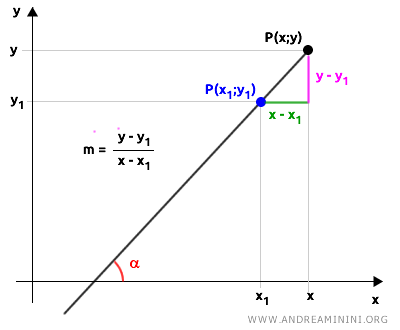
En esta ecuación, $ m $ es la pendiente de la recta, $ (x_1, y_1) $ son las coordenadas de un punto conocido por el que pasa la recta, y $ (x, y) $ representan cualquier otro punto que pertenece a ella.
Nota. La ecuación $ y = m \cdot (x - x_1) + y_1 $ es especialmente práctica para describir de manera geométrica una recta en el plano cartesiano, partiendo de un punto de referencia y su pendiente. También suele expresarse en la forma equivalente: $ y - y_1 = m \cdot (x - x_1) $.
Ejemplo Práctico
Supongamos que tenemos el punto (x1, y1) = (1, 3) y la pendiente m = 2.
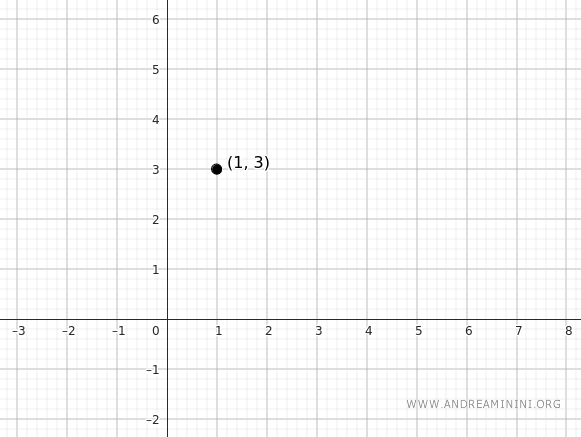
Aplicamos la ecuación de la recta que pasa por el punto dado con la pendiente conocida:
$$ y = m \cdot (x - x_1) + y_1 $$
Sustituyendo los valores x1 = 1, y1 = 3 y m = 2, obtenemos:
$$ y = 2 \cdot (x - 1) + 3 $$
$$ y = 2x - 2 + 3 $$
$$ y = 2x + 1 $$
Las variables x e y representan las coordenadas de todos los puntos que se encuentran sobre esta recta.
Podemos calcular algunos puntos específicos de la recta (distintos del inicial) utilizando una tabla de valores:
$$ \begin{array}{c|c} x & y = 2x + 1 \\ \hline -1 & -1 \\ 0 & 1 \\ 1 & 3 \\ 2 & 5 \end{array} $$
Así podemos determinar fácilmente las coordenadas de todos los puntos de la recta que pasa por el punto (1, 3) y tiene pendiente m = 2.
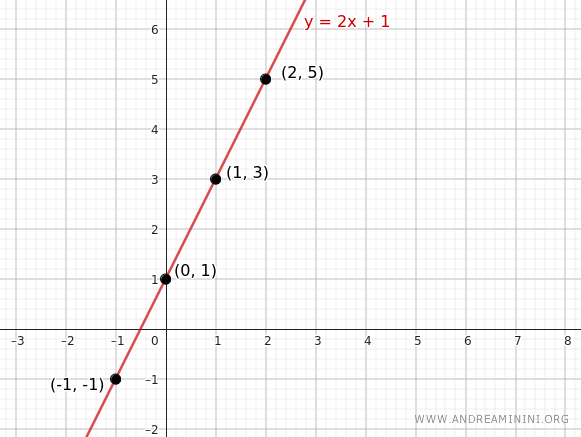
Nota. Desde el punto de vista geométrico, basta conocer las coordenadas de un segundo punto (x, y), distinto de (x1, y1), para poder trazar la recta que pasa por ambos. Un punto particularmente sencillo de calcular es la intersección con el eje y (ordenada al origen), que se obtiene sustituyendo x = 0 en la ecuación y = 2x + 1.
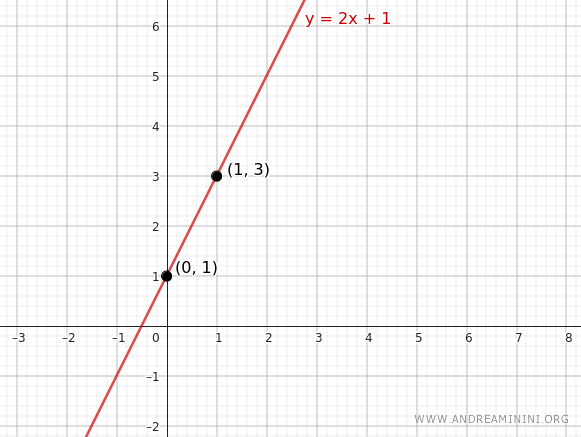
Demostración
La ecuación anterior se deduce de la ecuación de la recta que pasa por dos puntos (o de la condición de alineación).
$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$
Mediante una sencilla manipulación algebraica, se obtiene:
$$ \frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1} $$
Donde $ m = \frac{y_2 - y_1}{x_2 - x_1} $ es la pendiente de la recta.
Por lo tanto:
$$ m = \frac{y - y_1}{x - x_1} $$
Despejando y, se obtiene la ecuación de la recta que pasa por el punto (x1, y1) con pendiente m:
$$ y - y_1 = m(x - x_1) $$
$$ y = m(x - x_1) + y_1 $$
Y así sucesivamente.