Rectas paralelas

Dos rectas son paralelas si no se cortan en ningún punto o si coinciden en todos sus puntos.

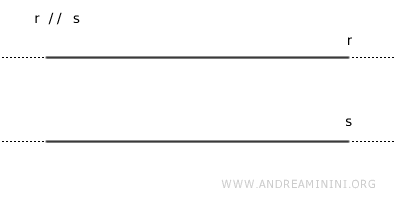
Los símbolos // o || se utilizan para indicar que dos rectas son paralelas.

$$ r // s $$ $$ r \parallel s $$

La región comprendida entre dos rectas paralelas se denomina franja o banda.

La distancia mínima entre un punto cualquiera de una recta y la otra se conoce como la altura de la franja o distancia entre rectas paralelas.

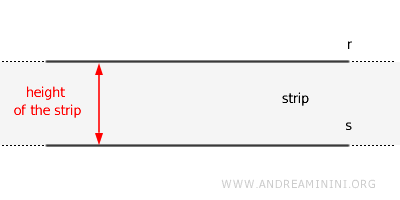
Esta altura corresponde a la distancia perpendicular entre ambas rectas, y se mantiene constante en todos sus puntos.

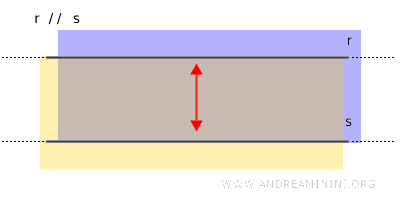
Nota. La región comprendida entre dos rectas paralelas distintas $ r $ y $ s $ también puede describirse como la intersección entre el semiplano delimitado por $ r $ que contiene a $ s $ y el semiplano delimitado por $ s $ que contiene a $ r $.

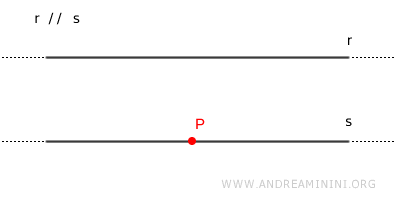
Quinto postulado de Euclides

Dado un punto $ P $ que no pertenece a una recta $ r $, existe una única recta $ s $ tal que $ s \parallel r $.

El quinto postulado de Euclides, conocido como el postulado de las paralelas, es el más célebre - y también el más controvertido - de sus axiomas.

A diferencia de los otros cuatro, no resulta evidente de forma inmediata ni se deduce de la intuición geométrica.

En términos precisos, es posible demostrar que por un punto exterior a una recta $ r $ pasa al menos una recta paralela a ella, pero no se puede demostrar que sea la única.

¿Qué se deduce del postulado?

Del postulado se derivan numerosas propiedades geométricas fundamentales relacionadas con las rectas paralelas.

• Teorema de transitividad del paralelismo
  Si dos rectas $a$ y $b$ son paralelas a una tercera recta $c$, entonces también son paralelas entre sí: $$ a \parallel c \ , \ b \parallel c \ \Rightarrow a \parallel b $$

  Demostración. Procedemos por contradicción. Supongamos que $a$ y $b$ son paralelas a $c$, pero no son paralelas entre sí: $$ a \parallel c $$ $$ b \parallel c $$ Si $a$ y $b$ no fueran paralelas, se cortarían en un punto $P$.
  
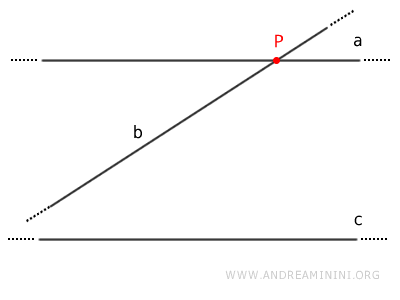
  Sin embargo, según la hipótesis, tanto $a$ como $b$ son paralelas a $c$. Eso implicaría que por el punto $P$ pasan dos rectas distintas, ambas paralelas a $c$, lo cual contradice el postulado de las paralelas. Por tanto, $a$ y $b$ no pueden intersectarse. La hipótesis inicial es falsa, y su negación es verdadera: las rectas $a$ y $b$, además de ser paralelas a $c$, también son paralelas entre sí (a // b)
  

• El paralelismo como relación de equivalencia
  El conjunto de todas las rectas paralelas a una dada $r$ se denomina dirección. Este conjunto forma una clase de equivalencia, ya que todas las rectas del grupo son mutuamente paralelas y constituyen un haz de rectas. En consecuencia, el paralelismo define una relación de equivalencia, pues cumple con las tres propiedades fundamentales: reflexividad, simetría y transitividad.
  • Reflexividad
    Toda recta es paralela a sí misma. $$ r \parallel r $$

    Nota. Esta propiedad está implícita en la definición misma de paralelismo.

  • Simetría
    Si una recta $r$ es paralela a otra recta $s$, entonces $s$ también lo es a $r$. $$ r \parallel s $$

    Nota. Esto se deduce directamente de la simetría de la relación.

  • Transitividad
    Si $r$ es paralela a $s$, y $s$ lo es a $p$, entonces $r$ también es paralela a $p$. $$ r \parallel s \ , \ s \parallel p \ \Rightarrow r \parallel p $$

    Nota. Esta propiedad se fundamenta en el teorema que afirma que dos rectas paralelas a una misma tercera recta son también paralelas entre sí.

• Teorema de la recta que corta un haz de paralelas
  Si una recta $ r $ corta a una recta $ a $ perteneciente a un haz impropio de rectas paralelas $ a \parallel b \parallel c \dots $, entonces debe cortar también a todas las demás rectas del haz.
  

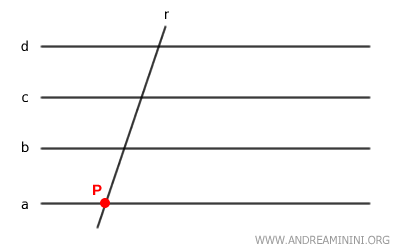
  Demostración. Consideremos un haz impropio de rectas paralelas: $$ a \parallel b \parallel c \parallel \dots $$ y una recta $ r $ que intersecta a $ a $ en un punto $ P $: $$ r \cap a = \{ P \} $$ Queremos probar que $ r $ también corta a todas las demás rectas del haz. Supongamos lo contrario: que $ r $ no corta a una de ellas, digamos $ b $: $$ r \cap b = \emptyset $$ Esto significaría que $ r $ es paralela a $ b $: $$ r \parallel b $$ Pero como $ b \parallel a $, por transitividad tendríamos: $$ r \parallel a $$ Lo cual contradice el hecho de que $ r $ y $ a $ se cruzan en el punto $ P $. Por tanto, la suposición $$ r \cap b = \emptyset $$ es falsa, y debe cumplirse que: $$ r \cap b \ne \emptyset $$ Este razonamiento se puede aplicar a cualquier recta del haz. Por tanto, $ r $ debe cortar a todas las rectas del conjunto.

Condición necesaria y suficiente para que dos rectas sean paralelas

Para que dos rectas sean paralelas, deben cumplirse dos condiciones fundamentales:

Coplanaridad

Dos rectas paralelas deben estar contenidas en un mismo plano; es decir, deben ser coplanares.

Si no son coplanares, no pueden ser paralelas.

Por tanto, la coplanaridad es una condición necesaria, aunque no suficiente.

Por ejemplo, en el espacio tridimensional, si dos rectas no se encuentran en el mismo plano, se denominan rectas alabeadas y, por definición, no pueden ser paralelas.

No intersección

Para que dos rectas sean paralelas, además de ser coplanares, no deben cortarse en ningún punto.

Dicho de otro modo: deben estar en el mismo plano y no compartir ningún punto.

Esta es la condición necesaria y suficiente para que dos rectas sean paralelas.

Si dos rectas están en el mismo plano y no se intersectan, entonces son paralelas por definición.

Teorema de las rectas paralelas

Este resultado también se conoce como el criterio de paralelismo entre rectas.

Su recíproco también es válido: si dos rectas son paralelas, entonces cualquier transversal que las corte generará pares de ángulos alternos congruentes, ángulos correspondientes congruentes y ángulos conjugados suplementarios.

Definición alternativa

Dos rectas (que no sean verticales) son paralelas si tienen la misma pendiente, y viceversa.

Es decir, son paralelas si tienen la misma inclinación respecto al eje x.

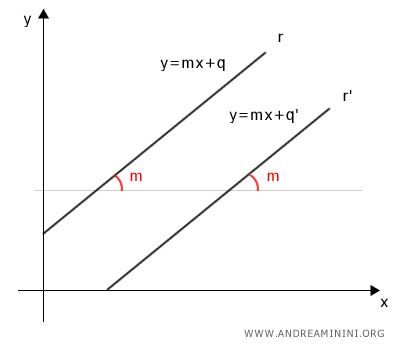
Las rectas verticales (paralelas al eje y) son casos especiales, ya que su pendiente no está definida.

Teorema recíproco. Si dos rectas tienen la misma pendiente (m = m'), entonces son paralelas.

Ejemplo práctico con demostración

Consideremos dos rectas paralelas: r: y = 2x - 2 y r': y = 2x - 6

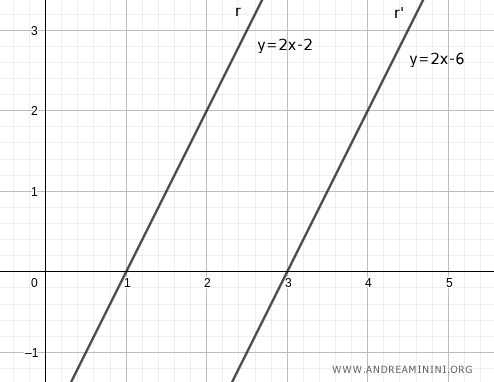
Sean x₁ y x₁' los puntos en los que las rectas cortan el eje x.

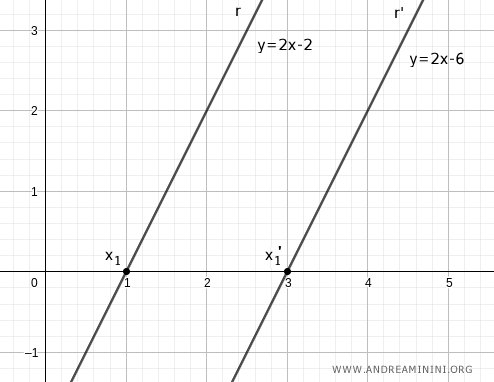
Elegimos otros dos puntos sumando una constante k a x₁ y x₁'. Por ejemplo, si k = 1:

$$ x_2 = x_1 + k \qquad x_2' = x_1' + k $$

Los segmentos x₁x₂ y x₁'x₂' tienen, por tanto, la misma longitud.

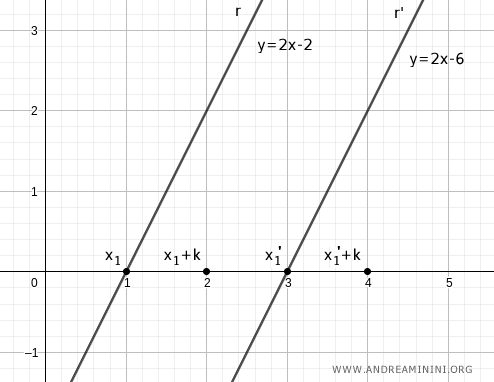
Desde esos nuevos puntos, trazamos perpendiculares que cortan a las rectas r y r'.

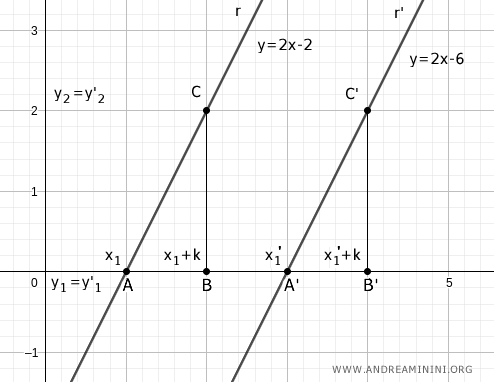
Esto genera dos triángulos rectángulos: ABC y A'B'C'.

Ambos comparten un ángulo recto α = α'.

Según el teorema del paralelismo, los ángulos β = β' también son congruentes, ya que son correspondientes al estar determinadas por la misma transversal (el eje x).

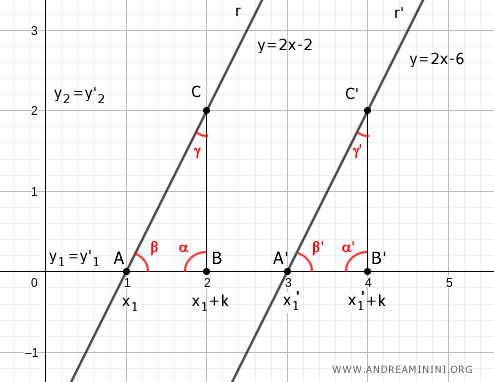
De acuerdo con el segundo criterio de congruencia, los triángulos ABC y A'B'C' son congruentes: tienen un lado correspondiente igual AB ≅ A'B' y dos ángulos adyacentes iguales.

Nota. Al ser ambos triángulos rectángulos, comparten un ángulo de 90°, y los ángulos formados por la transversal también son congruentes. Por lo tanto, el tercer ángulo también es igual (γ = γ').

Como los triángulos son congruentes, todos sus lados correspondientes son iguales:

$$ \overline{AB} \cong \overline{A'B'} \qquad \overline{BC} \cong \overline{B'C'} $$

Como AB = x₂ - x₁ y A'B' = x₂' - x₁', y los segmentos verticales también son iguales, entonces:

$$ \frac{y_2 - y_1}{x_2 - x_1} = \frac{y'_2 - y'_1}{x'_2 - x'_1} $$

Por tanto, las pendientes son iguales:

$$ m = m' $$

Demostración del teorema recíproco. Partiendo de que m = m', se deduce que los triángulos formados son congruentes y, por tanto, las rectas son paralelas.

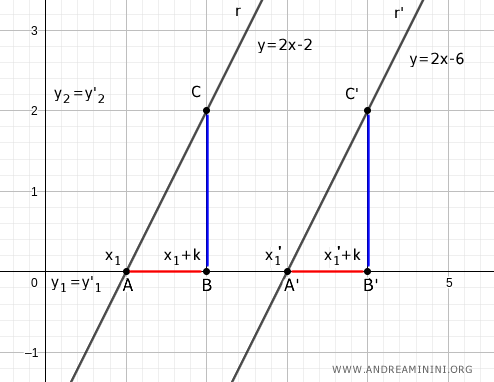
Si m = m' y sabemos que m = BC / AB y m' = B'C' / A'B', entonces: $$ \frac{BC}{AB} = \frac{B'C'}{A'B'} $$

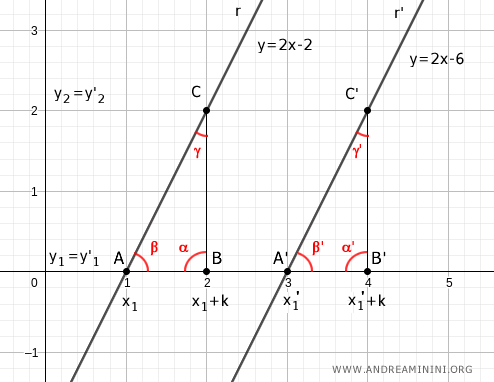
Si AB ≅ A'B' y BC ≅ B'C', y el ángulo entre ellos es recto, entonces los triángulos son congruentes por el primer criterio de congruencia. En particular, los ángulos β y β' son iguales y miden la inclinación respecto al eje x. Por tanto, r y r' son paralelas: r // r'.

Condición de paralelismo entre rectas en forma implícita

Sean $ r $ y $ s $ dos rectas cuyas ecuaciones implícitas son: $$ r: \ ax + by + c = 0 $$ $$ s: \ a'x + b'y + c' = 0 $$ Entonces $ r // s $ si se cumple la condición: $$ ab' - a'b = 0 $$ Esta condición también puede expresarse como: $$ \frac{a}{a'} = \frac{b}{b'} $$

Se conoce como la condición de paralelismo entre rectas.

Ejemplo

Consideremos dos rectas:

$$ r: \ 2x + 3y + 1 = 0 $$

$$ s: \ 4x + 6y - 8 = 0 $$

Verificamos si cumplen la condición:

$$ ab' - a'b = 2 \cdot 6 - 4 \cdot 3 = 12 - 12 = 0 $$

Como se cumple la igualdad, concluimos que las dos rectas son paralelas: $ r // s $.

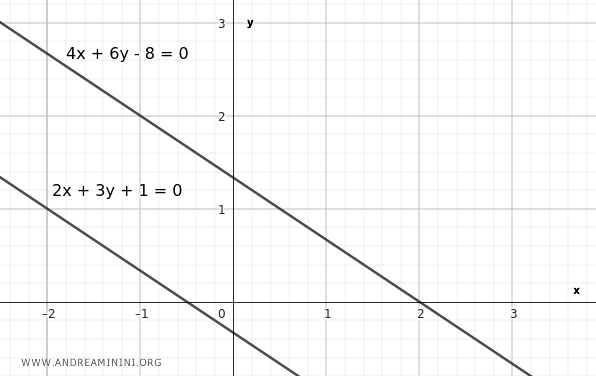
Demostración

Sean dos rectas paralelas $ r // s $ definidas por:

$$ r: \ ax + by + c = 0 \qquad s: \ a'x + b'y + c' = 0 $$

Sus pendientes son, respectivamente:

$$ m = - \frac{a}{b} \qquad m' = - \frac{a'}{b'} $$

Como r y s son paralelas, se cumple: $$ m = m' $$

Por tanto: $$ - \frac{a}{b} = - \frac{a'}{b'} \Rightarrow \frac{a}{b} = \frac{a'}{b'} \Rightarrow ab' = a'b $$

Con esto se concluye la demostración.

Cómo saber si dos rectas paralelas son distintas o coincidentes

Dos rectas son paralelas distintas si cumplen la condición de paralelismo pero no la de coincidencia: $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$ En cambio, si se verifican ambas condiciones, las rectas coinciden, es decir, representan la misma línea: $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$

Tanto las rectas paralelas distintas como las coincidentes satisfacen la condición de paralelismo:

$$ \frac{a}{a'} = \frac{b}{b'} $$

donde \( a, b, a', b' \) son los coeficientes de las variables \( x \) e \( y \) en las ecuaciones de ambas rectas:

$$ r: ax + by + c = 0 \qquad r': a'x + b'y + c' = 0 $$

En otras palabras, las rectas coincidentes son un caso particular de paralelismo, ya que tienen la misma pendiente y, además, comparten todos sus puntos.

Para distinguir si dos rectas paralelas son coincidentes o simplemente distintas, se debe comprobar también la condición de coincidencia, comparando la razón entre sus términos independientes: \( \frac{c}{c'} \).

• Rectas coincidentes
  Si la razón entre los términos constantes es igual a la de los coeficientes, las rectas son coincidentes: $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$ En este caso, ambas representan exactamente la misma recta.
• Rectas paralelas distintas
  Si la razón entre los términos constantes no coincide con la de los coeficientes, las rectas son paralelas pero no coinciden: $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$ Esto significa que nunca se cruzan, pero no comparten ningún punto.

Ejemplo

Consideremos las siguientes ecuaciones en forma general:

$$ r: 2x + 3y + 6 = 0 \qquad r': 4x + 6y + 12 = 0 $$

Queremos determinar si estas rectas son secantes, paralelas distintas o coincidentes.

Primero, comprobamos la condición de paralelismo:

$$ \frac{2}{4} = \frac{3}{6} = \frac{1}{2} $$

Como se cumple, podemos afirmar que las rectas no se cortan: son paralelas.

A continuación, analizamos la condición de coincidencia evaluando la razón entre los términos constantes:

$$ \frac{6}{12} = \frac{1}{2} $$

Al coincidir también esta tercera razón, concluimos que las rectas son coincidentes: $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{1}{2} $$

Por lo tanto, ambas ecuaciones representan exactamente la misma recta.

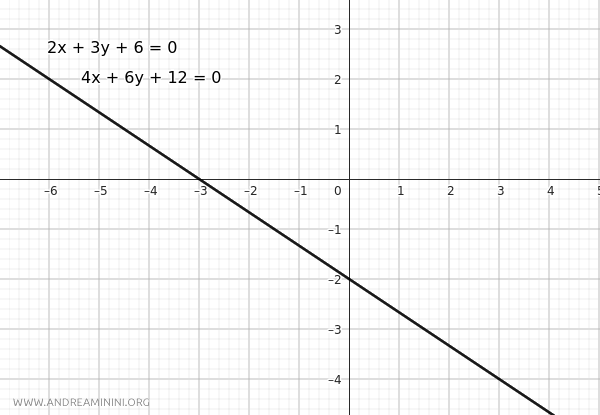
Este método permite identificar la relación entre dos rectas - sin resolver ningún sistema - simplemente comparando las razones entre sus coeficientes.

Ejemplo de rectas paralelas distintas. Veamos ahora un ejemplo donde las rectas son paralelas pero no coincidentes: $$ r: 2x + 3y + 6 = 0 \qquad r': 4x + 6y + 3 = 0 $$ Comprobamos primero la condición de paralelismo: $$ \frac{2}{4} = \frac{3}{6} = \frac{1}{2} $$ pero la razón entre los términos independientes es distinta: $$ \frac{6}{3} = 2 \ne \frac{1}{2} $$ En este caso: $$ \frac{a}{a'} = \frac{b}{b'} \ne \frac{c}{c'} $$ Por tanto, las rectas son paralelas entre sí, pero distintas.

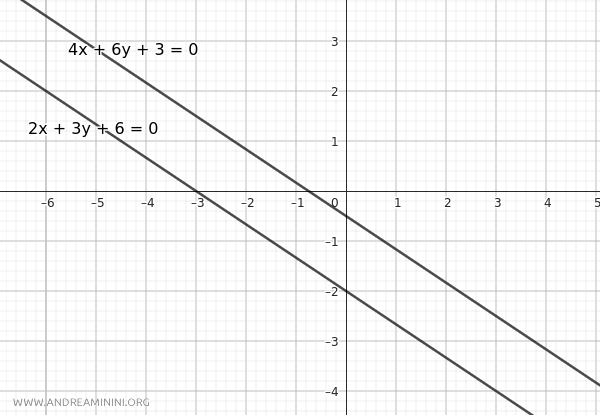
Observaciones

• La distancia entre dos rectas paralelas es constante
  Si trazamos segmentos perpendiculares desde distintos puntos de una recta \( r \) hacia otra paralela \( s \), todos tendrán la misma longitud.
  
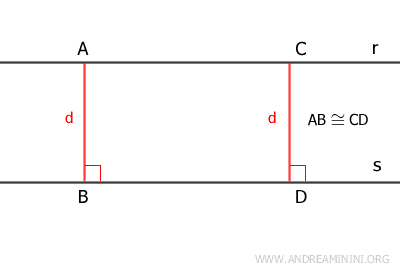
  Es decir, la separación entre dos rectas paralelas es siempre uniforme.

  Demostración. Sean \( r // s \) y dos perpendiculares \( AB \) y \( CD \) trazadas entre ellas. Se forma el rectángulo \( ABCD \). En cualquier rectángulo, los lados opuestos son congruentes, por lo tanto \( AB \cong CD \), lo que prueba que la distancia es constante.
  
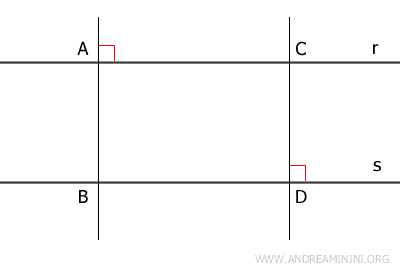
  Otra demostración. Tomamos dos puntos \( A \) y \( C \) en \( r \), y desde ellos trazamos perpendiculares a \( s \) que interceptan en \( B \) y \( D \). Unimos \( A \) con \( D \).
  
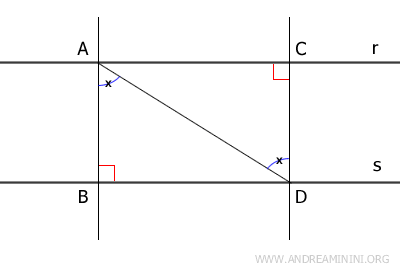
  Los triángulos \( \triangle ABD \) y \( \triangle ACD \) son congruentes por el criterio ASA: comparten el lado \( AD \), tienen ángulos rectos y un par de ángulos alternos internos iguales. Por tanto, \( AB \cong CD \).

• Dos rectas perpendiculares a una tercera son paralelas
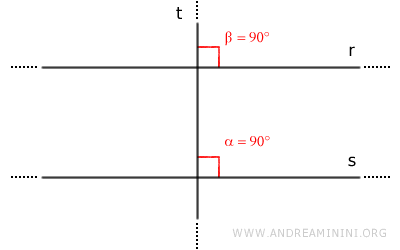
  Si \( r \) y \( s \) son perpendiculares a la misma recta \( t \), entonces \( r // s \).
  
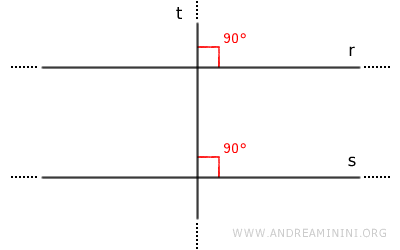
  Basta observar que generan ángulos correspondientes o alternos congruentes, por lo tanto son paralelas.

  Demostración. Supongamos que \( r \) y \( s \) se cortan en un punto. Entonces existirían dos rectas diferentes perpendiculares a \( t \) pasando por el mismo punto, lo que contradice la unicidad de la perpendicular. Por tanto, deben ser paralelas.

• Postulado de las paralelas
  Dado un punto \( P \) fuera de una recta \( r \), existe una única recta que pasa por \( P \) y es paralela a \( r \).
  
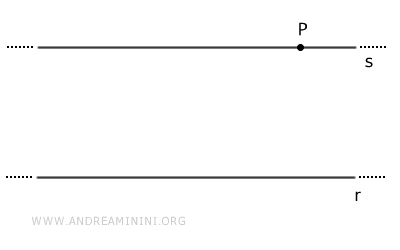
• Una recta perpendicular a \( r \) lo es también a toda recta paralela a \( r \)
  Si \( t \) es perpendicular a \( s \), y \( s // r \), entonces \( t \) también es perpendicular a \( r \).

  Demostración. Sean \( r // s \) y \( t \perp s \). Entonces forman un ángulo recto \( \alpha = 90^\circ \).
  
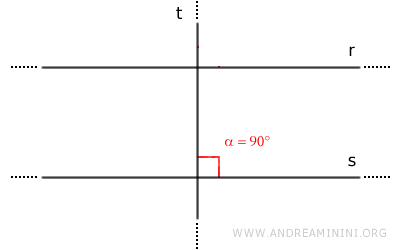
  Como \( r \) y \( s \) son paralelas, forman ángulos correspondientes iguales con \( t \), por tanto \( \beta = 90^\circ \) y \( t \perp r \).
  

• Las paralelas a dos rectas secantes también se cortan
  

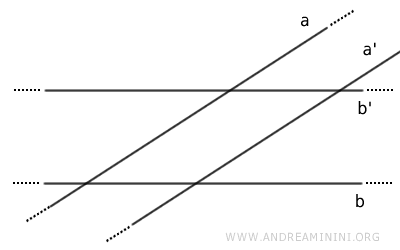
  Demostración. Supongamos que \( a \) y \( b \) se cortan, y que sus paralelas \( a' \) y \( b' \) fuesen paralelas entre sí: $$ a \parallel a' \qquad b \parallel b' \qquad a' \parallel b' $$ Entonces, por transitividad: $$ a \parallel b $$ lo cual contradice el hecho de que \( a \) y \( b \) se intersectan. Luego, \( a' \) y \( b' \) también deben cortarse.

• Teorema de los planos paralelos cortados por un tercer plano
  Si un plano \( \pi \) corta dos planos paralelos \( \pi_1 \) y \( \pi_2 \), las intersecciones son dos rectas paralelas.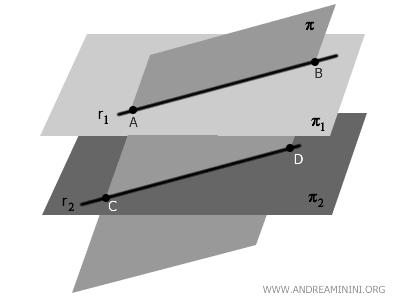

  Esto se debe a que \( \pi_1 \) y \( \pi_2 \) están a la misma distancia y son cortados con el mismo ángulo por \( \pi \). Por tanto, sus intersecciones son rectas paralelas.

Y así sucesivamente.