Primer teorema de congruencia de triángulos
El primer teorema de congruencia de triángulos establece que dos triángulos son congruentes si tienen dos lados y el ángulo comprendido entre ellos congruentes y en el mismo orden.
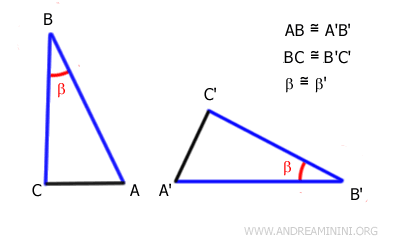
En otras palabras, dos triángulos son congruentes cuando poseen dos lados y el ángulo comprendido entre ellos con medidas idénticas.
Este teorema también se conoce como criterio Lado-Ángulo-Lado (LAL) o SAS (Side-Angle-Side).
Veamos, por ejemplo, estos dos triángulos ABC y A'B'C'.
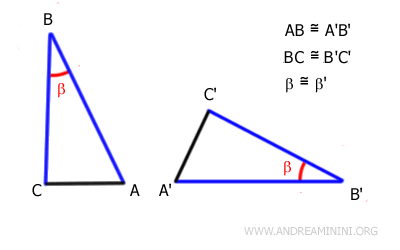
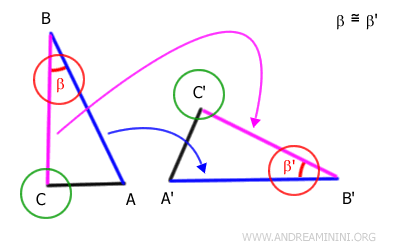
Los lados AB y BC del triángulo ABC son congruentes, respectivamente, con los lados A'B' y B'C' del triángulo A'B'C'; es decir, tienen la misma longitud aunque estén dispuestos de forma distinta.
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
Además, los ángulos β y β', formados por estos pares de lados, también son congruentes, es decir, tienen la misma medida:
$$ \beta \cong \beta' $$
Por lo tanto, según el primer teorema de congruencia, los dos triángulos son congruentes.
Si el ángulo congruente no está comprendido entre los dos lados, los triángulos no tienen por qué ser congruentes. Por ejemplo, considera el triángulo ABC. Se traza una circunferencia de radio AC con centro en A. El arco corta la prolongación de AC en el punto D, generando así el triángulo ACD.
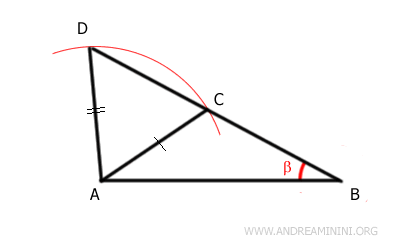
Es evidente que los triángulos ABC y ABD no son congruentes, ya que no pueden superponerse: el triángulo ABD es más grande que el triángulo ABC. Sin embargo, ambos triángulos presentan dos lados congruentes (AB ≅ AB y AC ≅ AD), así como un ángulo congruente β. Pero dicho ángulo no está comprendido entre los lados congruentes. En conclusión, disponer de dos lados y un ángulo no comprendido entre ellos no garantiza la congruencia.
Ilustración del postulado
El primer criterio de congruencia de triángulos se establece como un postulado porque se fundamenta en los axiomas esenciales de Euclides.
Por lo tanto, lo que se presenta a continuación no constituye una demostración formal estricta, ya que los movimientos rígidos se entienden como transformaciones geométricas intuitivas.
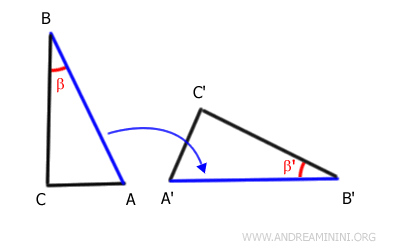
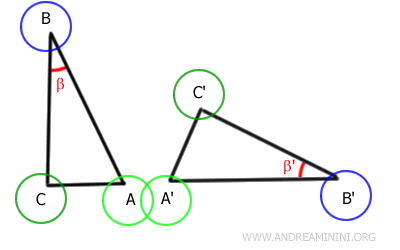
Consideremos dos triángulos, ABC y A'B'C'
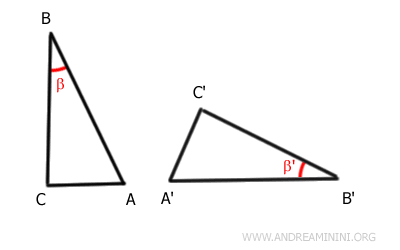
Según la hipótesis, los segmentos AB y A'B', así como BC y B'C', tienen la misma longitud, y los ángulos comprendidos β y β' son congruentes.
Aplicamos ahora un movimiento rígido - una combinación de rotación y traslación - que hace coincidir el lado AB con el lado A'B', de modo que el ángulo β también se alinee perfectamente con el ángulo β'.
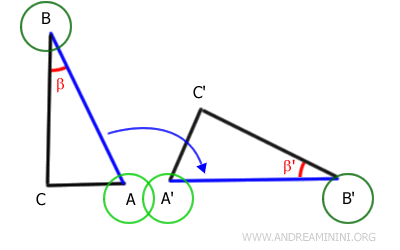
Como AB se superpone exactamente con A'B', sus extremos deben coincidir.
En consecuencia, el punto A coincide con el punto A' y el punto B con el punto B'.
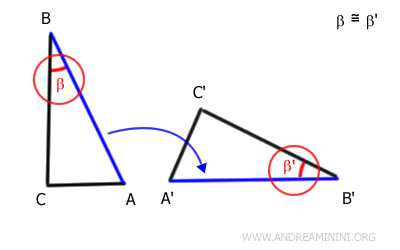
Dado que los ángulos β y β' están situados junto a los lados ya alineados, también se superponen perfectamente. Esto confirma que tienen la misma amplitud, es decir, son congruentes.
Como el ángulo comprendido es congruente y los lados adyacentes son iguales, el segmento BC debe coincidir exactamente con el segmento B'C'.
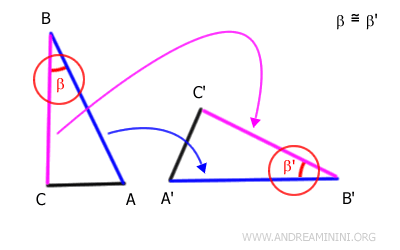
Esto implica que sus extremos también se corresponden.
Ya habíamos establecido que el punto B coincide con el punto B'; ahora comprobamos que el punto C coincide con el punto C'.
De ello se sigue que el segmento AC también debe coincidir con A'C', ya que sus extremos se superponen completamente.
En conclusión, todos los vértices correspondientes de ambos triángulos coinciden tras la transformación rígida. Esto implica que todos sus lados y ángulos son congruentes, en el mismo orden.
Por tanto, podemos afirmar que los dos triángulos son congruentes.
Y así sucesivamente.