Fórmula de Herón
¿Alguna vez te has preguntado cómo calcular el área de un triángulo conociendo únicamente las longitudes de sus lados? ¡La fórmula de Herón es la herramienta perfecta para lograrlo! Su expresión es sorprendentemente sencilla: $$ A = \sqrt{p(p-a)(p-b)(p-c)} $$ Aquí, \(a\), \(b\) y \(c\) representan los lados del triángulo, mientras que \(p\) es el semiperímetro.
El semiperímetro, aunque suene sofisticado, no es más que la mitad del perímetro del triángulo:
$$ p = \frac{a+b+c}{2} $$
Lo que hace tan valiosa la fórmula de Herón es que no depende de la altura ni de los ángulos, permitiendo calcular el área de forma directa y precisa.
En definitiva, es una auténtica salvación cuando medir la altura resulta un verdadero desafío.
Dato interesante: Esta fórmula recibe su nombre de Herón de Alejandría, un brillante matemático e ingeniero griego del siglo I d.C. No obstante, se cree que este ingenioso método pudo haber sido conocido incluso antes de su época.
No importa qué tipo de triángulo tengas entre manos: escaleno, isósceles o equilátero; mientras conozcas las longitudes de sus lados, podrás utilizar la fórmula de Herón sin problemas.
¡Pongámosla en práctica!
Veamos cómo funciona con un triángulo cuyos lados miden 8, 15 y 17 unidades.
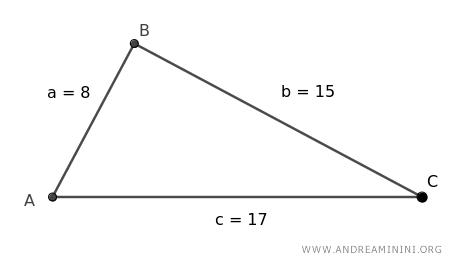
Nuestro objetivo: calcular el área de este triángulo.
Como no disponemos de la altura, la fórmula clásica de base por altura no es útil en este caso.
$$ A = \frac{ \text{base} \times \text{altura} }{2} $$
Sin embargo, no hay motivo para preocuparse: contamos con las longitudes de sus tres lados.
Es el momento perfecto para recurrir a la fórmula de Herón.
$$ A = \sqrt{p(p-a)(p-b)(p-c)} $$
Donde \(a\), \(b\) y \(c\) son los lados, y \(p\) es el semiperímetro.
Sustituyamos los valores: a = 8, b = 15 y c = 17.
\[A = \sqrt{p(p - 8)(p - 15)(p - 17)}\]
Primero, calculamos el semiperímetro \(p\), sumando las longitudes de los lados y dividiéndolas entre dos.
$$ p = \frac{a + b + c}{2} $$
$$ p = \frac{8 + 15 + 17}{2} = \frac{40}{2} = 20 $$
Curiosidad: ¿Por qué usar el semiperímetro? Es una especie de valor intermedio que vincula las longitudes de los lados con el área, facilitando el cálculo.
Con \( p = 20 \), seguimos con el cálculo del área:
$$ A = \sqrt{20(20 - 8)(20 - 15)(20 - 17)} $$
$$ A = \sqrt{20 \times 12 \times 5 \times 3} = \sqrt{3600} = 60 $$
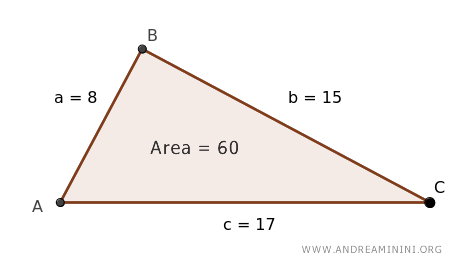
¡Y ahí lo tienes! El triángulo con lados de 8, 15 y 17 unidades tiene un área de 60 unidades cuadradas.
Una comprobación rápida en GeoGebra confirma que el resultado es correcto.
¿Sabías que…? La raíz cuadrada en la fórmula de Herón no es un mero adorno. Es el elemento clave que equilibra la relación entre el semiperímetro y las diferencias de las longitudes de los lados, permitiendo obtener el área exacta.
¡Y con esto, misión cumplida!