Teorema de la recta paralela a un lado de un triángulo

Una recta paralela a uno de los lados de un triángulo corta a los otros dos lados, dividiéndolos en segmentos proporcionales.

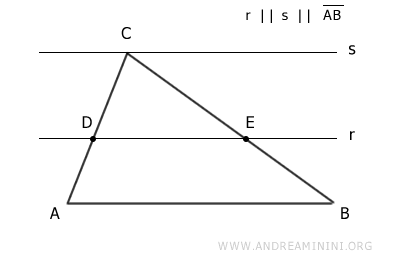
Este resultado se deduce del teorema de Tales.

Establece que, si una recta es paralela a uno de los lados de un triángulo y corta a los otros dos, entonces los divide en segmentos proporcionales.

Es uno de los fundamentos esenciales en el estudio de la semejanza de triángulos.

La recíproca también es válida

Si una recta corta dos lados de un triángulo y los divide en segmentos proporcionales, entonces dicha recta es paralela al tercer lado.

Este teorema, por tanto, proporciona un criterio geométrico para determinar el paralelismo entre rectas en el plano euclídeo. Es decir, nos permite establecer si una recta es paralela a otra mediante una simple relación de proporcionalidad.

Nota. Este principio es ampliamente utilizado en geometría plana para justificar el paralelismo de rectas y resolver problemas relacionados con triángulos semejantes. Asimismo, se extiende naturalmente a ámbitos más avanzados como la geometría proyectiva o la teoría de las proporciones.

Un ejemplo práctico

Consideremos, por ejemplo, un triángulo ABC.

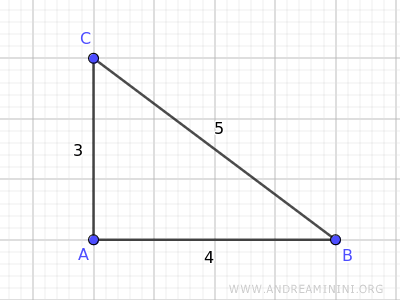
Se conocen las longitudes de sus lados: AB = 4, BC = 5 y AC = 3.

Ahora trazamos una recta paralela al lado AB que intersecta a los otros dos lados en los puntos D y E.

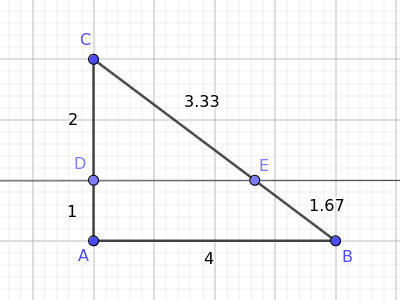
Dicha recta corta los lados AC y BC en los puntos D y E, respectivamente.

• El segmento AC queda dividido en AD y DC, de longitudes 1 y 2.
• El segmento BC se divide en BE y EC, que miden 1,67 y 3,33.

Según el teorema de Tales, se cumple que AD/DC = BE/EC, es decir, ambos pares de segmentos son directamente proporcionales.

$$ \frac{ \overline{AD} }{ \overline{DC} } = \frac{ \overline{BE} }{ \overline{EC} } $$

Sustituyendo los valores conocidos: AD = 1, DC = 2, BE = 1,67 y EC = 3,33

$$ \frac{1}{2} = \frac{1.6\overline{7}}{3.\overline{33}} $$

$$ 0.5 = 0.5 $$

Las razones coinciden, lo cual confirma que los segmentos son directamente proporcionales.

Demostración del teorema

La demostración es bastante directa.

Tomamos un triángulo cualquiera, ABC.

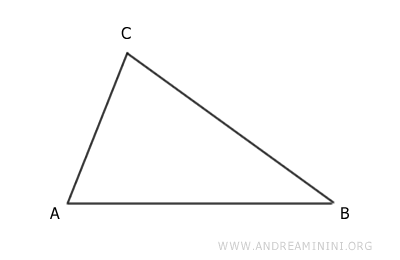
Se traza una recta paralela al lado AB, que corta a los lados AC y BC en los puntos D y E, respectivamente.

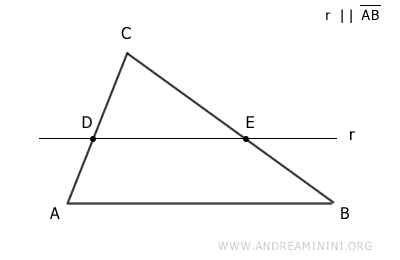
A continuación, se introduce una nueva recta s que pasa por el vértice opuesto al lado AB.

Las rectas AB, r y s constituyen un haz de paralelas que es cortado por las transversales AC y BC.

De acuerdo con el teorema de Tales, las divisiones en los lados AC y BC son proporcionales:

$$ AD:DC = BE:EC $$

Lo cual demuestra la validez del teorema.

Demostración de la recíproca

Como el teorema de Tales admite una recíproca, también lo hace este resultado derivado.

Por tanto, si una recta divide dos lados de un triángulo en segmentos proporcionales, se concluye que dicha recta es paralela al tercer lado.

Y así sucesivamente.