Segundo Teorema de Euclides
En un triángulo rectángulo, el área del cuadrado construido sobre la altura trazada a la hipotenusa es igual al área del rectángulo formado por las proyecciones de los catetos sobre dicha hipotenusa.
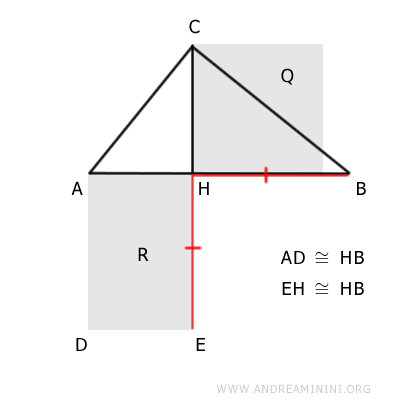
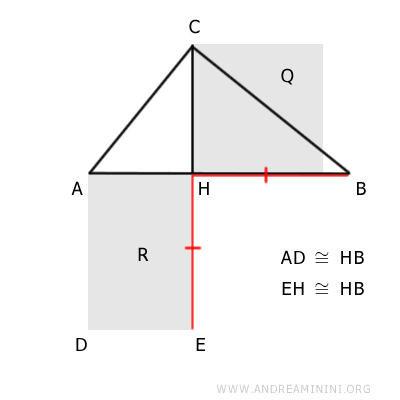
Dicho de otro modo, consideremos un cuadrado Q cuyo lado es igual a la altura CH del triángulo rectángulo respecto a la hipotenusa AB.
Las proyecciones de los catetos sobre la hipotenusa dividen a esta en dos segmentos, AH y BH. A partir de estos segmentos se construye un rectángulo R.
El cuadrado Q y el rectángulo R son polígonos equivalentes, es decir, poseen la misma área.
Corolario
Como corolario, en un triángulo rectángulo, la altura relativa a la hipotenusa es media proporcional entre las proyecciones de los catetos sobre dicha hipotenusa.
En términos de proporción, una proyección (p1) se relaciona con la altura (h) de la misma forma que la altura se relaciona con la otra proyección (p2) sobre la hipotenusa.
Nota: La proporción p1:h = h:p2 es equivalente al segundo teorema de Euclides: $$ p_1 : h = h : p_2 \rightarrow h^2 = p_1 \cdot p_2 $$ lo que indica que el área del cuadrado construido sobre la altura es igual al área del rectángulo formado por las proyecciones de los catetos sobre la hipotenusa.
Teorema Inverso
Si en un triángulo el cuadrado de la altura es igual al producto de las longitudes de los dos segmentos en que dicha altura divide al lado opuesto, entonces el triángulo es rectángulo. $$ \overline{CH}^2 = \overline{AH} \cdot \overline{BH} $$
En tal caso, el vértice (C) del cual se traza la altura forma un ángulo recto (90°).
Un Ejemplo
Consideremos el triángulo rectángulo ABC:
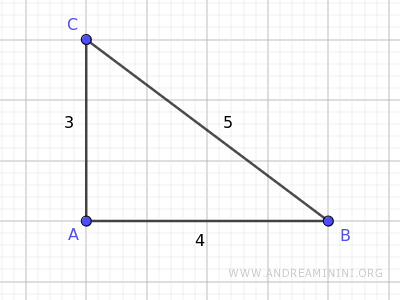
El triángulo rectángulo tiene catetos AB = 4 y AC = 3, y una hipotenusa BC = 5.
Se traza la altura del triángulo respecto a la hipotenusa.
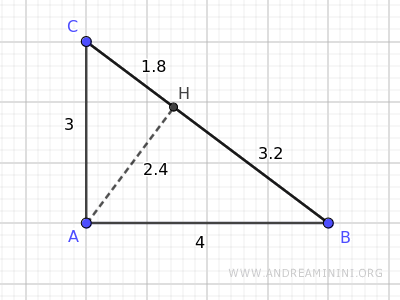
La altura AH del triángulo mide 2.4 y divide la hipotenusa en dos segmentos de longitudes 1.8 y 3.2.
El área del cuadrado construido sobre la altura es 5.76.
$$ \overline{AH}^2 = 2.4^2 = 5.76 $$
El área del rectángulo cuyos lados miden 1.8 y 3.2 es también 5.76.
$$ \overline{BH} \cdot \overline{CH} = 3.2 \cdot 1.8 = 5.76 $$
Por tanto, el cuadrado y el rectángulo tienen la misma área, es decir, son polígonos equivalentes.
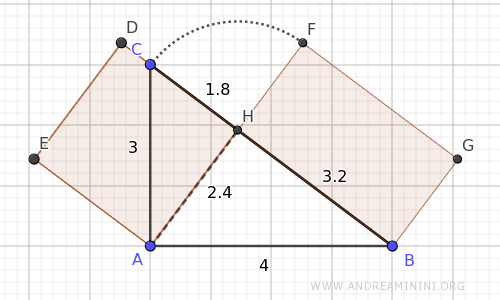
Demostración
Consideremos el triángulo rectángulo ABC.
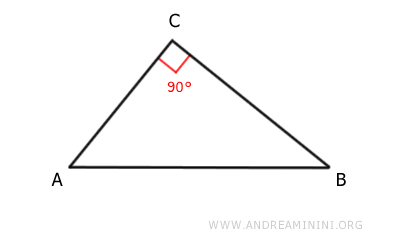
Los catetos del triángulo rectángulo son los segmentos AC y BC.
El segmento CH es la altura del triángulo respecto a la hipotenusa AB.
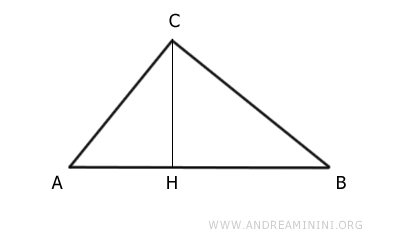
Se construye un cuadrado Q1 sobre la altura CH.
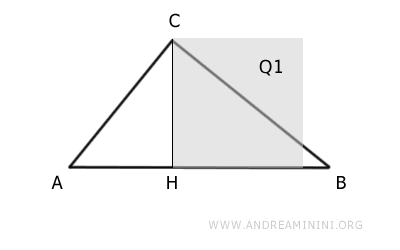
El punto H es también el pie de las proyecciones de los catetos, dividiendo la hipotenusa en dos segmentos AH y BH.
$$ \overline{AB} = \overline{AH} + \overline{BH} $$
Se construye un rectángulo R1 sobre el segmento AH, cuyos lados laterales son congruentes con AD≅EH≅AB, es decir, iguales a la longitud de la hipotenusa.
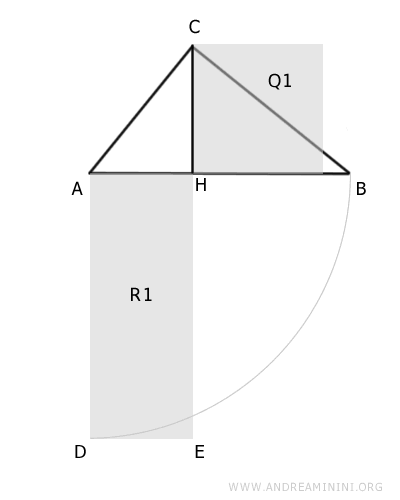
Podemos considerar el rectángulo R1 como un polígono compuesto por un cuadrado Q2, cuyo lado es congruente con AH, y un rectángulo R2.
$$ R1 \doteq Q2 + R2 $$
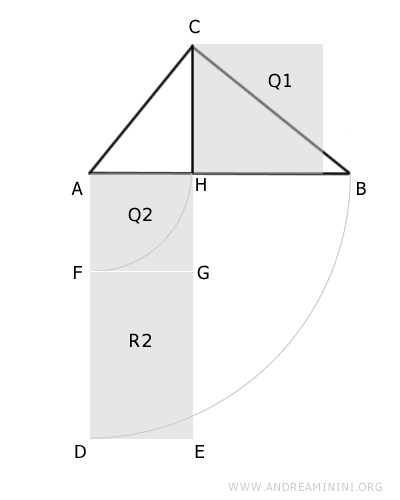
Es importante destacar que el rectángulo R2 tiene lados iguales a las proyecciones de los catetos del triángulo ABC sobre la hipotenusa, es decir, AH≅FG≅DE y BH≅FD≅EG.
$$ AH \cong FG \cong DE $$
$$ BH \cong FD \cong EG $$
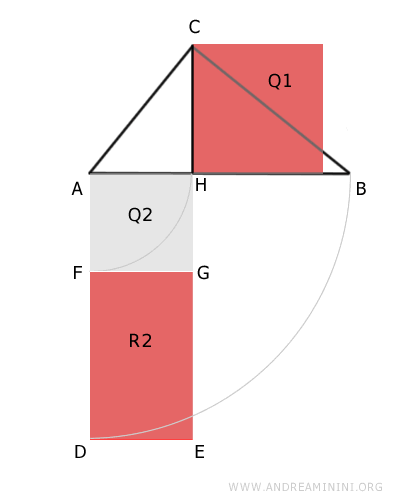
Por tanto, debemos demostrar que el cuadrado Q1 y el rectángulo R2 son polígonos equivalentes, es decir, tienen la misma área.
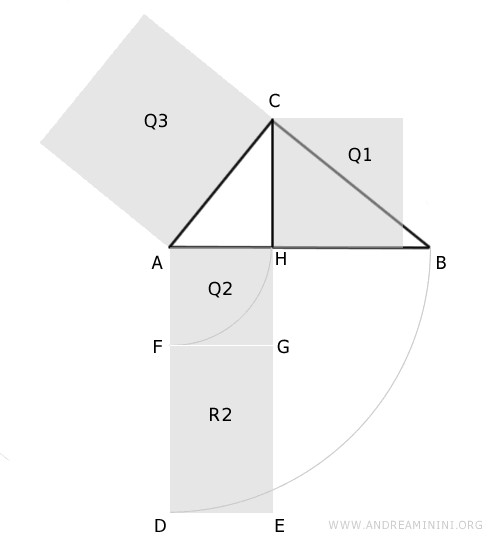
Observemos ahora el triángulo rectángulo AHC, que es parte integrante del triángulo ABC.
Según el Teorema de Pitágoras, la suma de los cuadrados de los catetos del triángulo AHC es igual al cuadrado construido sobre la hipotenusa AC.
$$ Q3 \doteq Q1 + Q2 $$
De esto se deduce que el área del cuadrado Q1 es igual a la diferencia entre Q3 y Q2.
$$ Q1 \doteq Q3 - Q2 $$
De acuerdo con el Primer Teorema de Euclides, el área Q3 es igual al área de R1 = Q2 + R2
$$ Q3 \doteq R1 $$
$$ Q3 \doteq Q2 + R2 $$
Por tanto, R2 también es equivalente a Q3 - Q2
$$ R2 \doteq Q3 - Q2 $$
En consecuencia, tanto Q1 como R2 son equivalentes a Q3 - Q2.
$$ R2 \doteq Q3 - Q2 \dot Q1 $$
Así, por la propiedad transitiva, Q1 y R2 son equivalentes, es decir, tienen la misma área.
$$ R2 \doteq Q1 $$
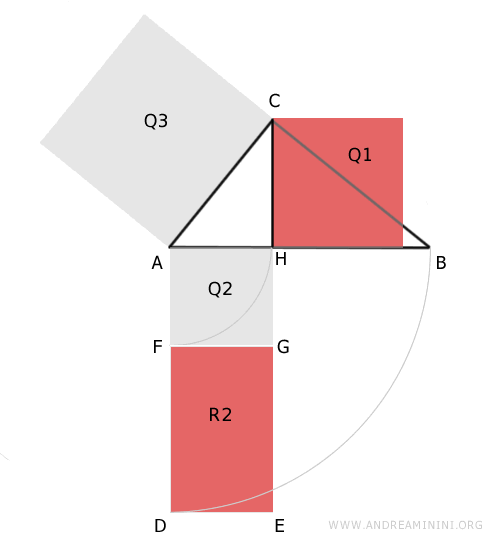
De este modo, se demuestra que el cuadrado Q1 construido sobre la altura CH respecto a la hipotenusa AB del triángulo ABC es equivalente al rectángulo R2, cuyos lados son iguales a las proyecciones AH≅FG y BH≅DF de los catetos.
Corolario
En un triángulo rectángulo, la altura (h) relativa a la hipotenusa es la media geométrica entre las proyecciones p1 y p2 de los catetos sobre dicha hipotenusa.
$$ p_1 : h = h : p_2 $$
Es decir, la proyección del cateto más corto (p1) se relaciona con la altura (h) de la misma manera en que esta se relaciona con la proyección del cateto más largo (p2).
Esto significa que el área del cuadrado construido sobre la altura es equivalente, es decir, igual, al área del rectángulo formado con una proyección como base y la otra como altura.
$$ \frac{p_1}{h} = \frac{h}{p_2} $$
$$ h^2 = p_1 \cdot p_2 $$
Así se confirma el segundo teorema de Euclides.
Ejemplo
Veamos un ejemplo con el triángulo rectángulo ABC, cuyas dimensiones son conocidas.
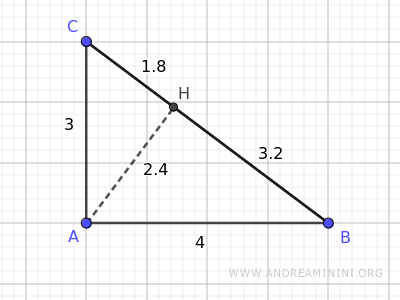
En este caso, la longitud del cateto más corto (AC) es 3, mientras que la del cateto más largo (AB) es 4.
La altura relativa a la hipotenusa mide 2.4.
De acuerdo con el corolario del segundo teorema de Euclides, se cumple la siguiente proporción:
$$ p_1 : h = h : p_2 $$
Sabemos que la altura (h) respecto a la hipotenusa mide 2.4.
$$ p_1 : 2.4 = 2.4 : p_2 $$
En este ejemplo, la proyección del cateto más corto (p1) sobre la hipotenusa mide 1.8, mientras que la proyección del cateto más largo (p2) mide 3.2.
$$ 1.8 : 2.4 = 2.4 : 3.2 $$
Si expresamos la proporción en forma de fracción y realizamos el cálculo, obtenemos:
$$ \frac{1.8}{2.4} = \frac{2.4}{3.2} $$
$$ 0.75 = 0.75 $$
Por lo tanto, la proporción se cumple perfectamente.
Demostración
Consideremos el triángulo rectángulo ABC.
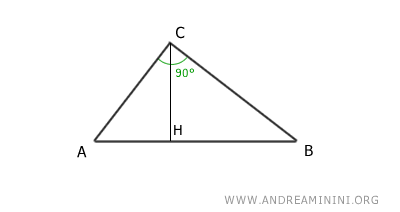
La altura relativa a la hipotenusa (CH) divide el ángulo recto en dos ángulos complementarios, γ1 y γ2, cuya suma es γ1 + γ2 = 90°.
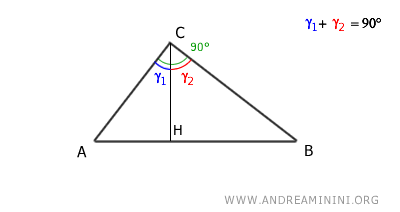
La altura CH divide el triángulo en dos triángulos rectángulos, ACH y CBH.
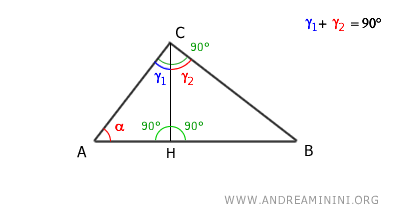
Sabiendo que la suma de los ángulos interiores de un triángulo es siempre 180°:
$$ \alpha + \gamma_1 + 90° = 180° $$
deducimos que, en el triángulo ACH, los ángulos α y γ1 son complementarios.
$$ \alpha + \gamma_1 = 180° - 90° $$
$$ \alpha + \gamma_1 = 90° $$
Como α + γ1 = 90° y γ1 + γ2 = 90°, se concluye que los ángulos α y γ2 son congruentes, es decir, α≅γ2, ya que ambos son complementarios de un mismo ángulo.
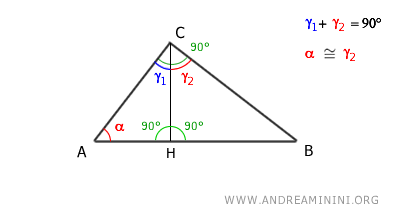
Por el primer criterio de semejanza de triángulos, los triángulos ACH y CBH son semejantes, puesto que comparten dos ángulos congruentes: el ángulo recto (90°) y los ángulos agudos α≅γ2.
$$ ACH \approx CBH $$
Al ser semejantes, los triángulos ACH y CBH tienen sus lados correspondientes en proporción.
$$ \overline{AC} : \overline{BC} = \overline{AH} : \overline{CH} = \overline{CH} : \overline{BH} $$
Esto demuestra el corolario del segundo teorema de Euclides.
$$ \overline{AH} : \overline{CH} = \overline{CH} : \overline{BH} $$
Aquí, AH es la proyección p1 del cateto más corto sobre la hipotenusa, mientras que BH es la proyección p2 del cateto más largo sobre la hipotenusa.
$$ p_1 : \overline{CH} = \overline{CH} : p_2 $$
Finalmente, CH es la altura del triángulo rectángulo ABC respecto a la hipotenusa.
$$ p_1 : h = h : p_2 $$
Y así sucesivamente.