Triángulo rectángulo con ángulos agudos de 30° y 60°
El triángulo rectángulo cuyos ángulos agudos miden 30° y 60° es exactamente la mitad de un triángulo equilátero.
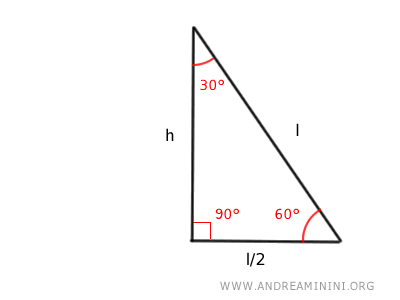
La altura (h) y el lado (l) de este triángulo rectángulo pueden determinarse mediante las siguientes fórmulas: $$ l = \frac{2h}{\sqrt{3}} $$ $$ h = \frac{l}{2} \sqrt{3} $$ La base (l/2) de este triángulo corresponde exactamente a la mitad del lado oblicuo (l), opuesto al ángulo recto.
Explicación
Si giro el triángulo rectángulo alrededor de su cateto mayor, obtengo un triángulo equilátero, es decir, un triángulo con tres ángulos de 60° y tres lados congruentes.
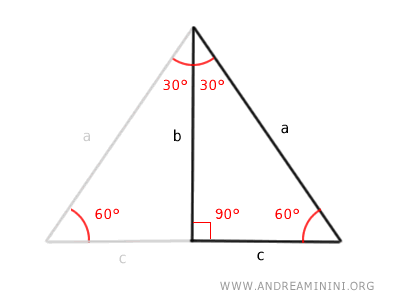
Una de las propiedades más importantes del triángulo rectángulo de 30°, 60° y 90° es que, conociendo la longitud de uno solo de sus lados, se pueden calcular las longitudes de los otros dos.
$$ a = \frac{2b}{\sqrt{3}} = \frac{2b \sqrt{3}}{3} $$
$$ b = \frac{a}{2} \sqrt{3} $$
$$ c = \frac{a}{2} $$
Esto es posible gracias a las relaciones trigonométricas entre sus lados y a la aplicación del teorema de Pitágoras.
Nota. Estas fórmulas son válidas exclusivamente para triángulos cuyos ángulos interiores son de 30°, 60° y 90°.
Demostración
Para demostrar las fórmulas del triángulo de 30°, 60° y 90°, se utiliza el teorema de Pitágoras.
Según este teorema, en un triángulo rectángulo, el cuadrado de la hipotenusa (a2) es igual a la suma de los cuadrados de los catetos (b2 + c2).
$$ a^2 = b^2 + c^2 $$
Dado que el triángulo rectángulo con ángulos de 30° y 60° equivale exactamente a la mitad de un triángulo equilátero, se deduce que el cateto c = a/2 es igual a la mitad de la hipotenusa, ya que en el triángulo equilátero todos los lados miden lo mismo (a = 2c).
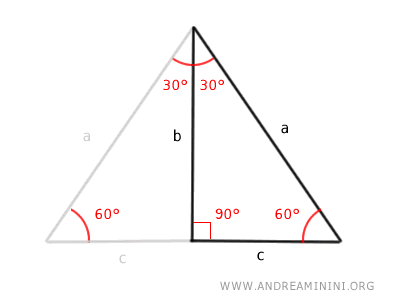
Así, puedo expresar el lado c = a/2 como la mitad de la hipotenusa (a).
$$ a^2 = b^2 + \left( \frac{a}{2} \right)^2 $$
Esta relación entre los lados del triángulo rectángulo permite resolverlo de distintas formas, según cuál de sus lados se conozca.
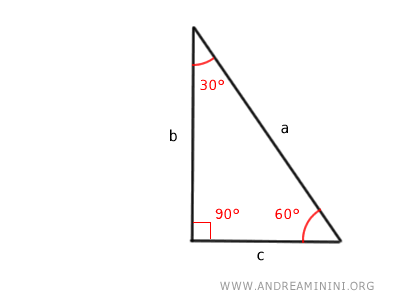
Por ejemplo, si conozco la hipotenusa (a), puedo calcular el valor de los otros catetos:
$$ b^2 = a^2 - \left( \frac{a}{2} \right)^2 $$
$$ b^2 = a^2 - \frac{a^2}{4} $$
$$ b^2 = \frac{4a^2 - a^2}{4} $$
$$ b^2 = \frac{3a^2}{4} $$
$$ \sqrt{b^2} = \sqrt{\frac{3a^2}{4}} $$
$$ b = \frac{a}{2} \sqrt{3} $$
El otro cateto (c) se calcula simplemente dividiendo la hipotenusa entre dos:
$$ c = \frac{a}{2} $$
Si, en cambio, conozco el cateto mayor (b), puedo determinar la hipotenusa (a) y, a partir de ella, el cateto menor (c = a/2).
$$ b^2 = a^2 - \left( \frac{a}{2} \right)^2 $$
$$ b^2 = a^2 - \frac{a^2}{4} $$
$$ b^2 = \frac{4a^2 - a^2}{4} $$
$$ b^2 = \frac{3a^2}{4} $$
$$ \frac{4b^2}{3} = a^2 $$
$$ \sqrt{\frac{4b^2}{3}} = \sqrt{a^2} $$
$$ \frac{2b}{\sqrt{3}} = a $$
Aplicando la propiedad invariativa de las fracciones, multiplico numerador y denominador por √3:
$$ \frac{2b}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = a $$
$$ \frac{2b \cdot \sqrt{3}}{3} = a $$
Una vez conocida la hipotenusa (a), obtengo el cateto menor, sabiendo que c = a/2.
$$ c = \frac{a}{2} $$
Y así sucesivamente.