Triángulo Equilátero

Un triángulo se llama triángulo equilátero cuando sus tres lados tienen exactamente la misma longitud.

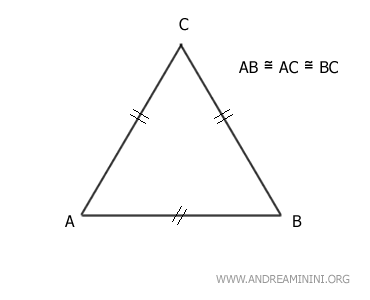
Es decir, un triángulo equilátero tiene los tres lados iguales en medida.

La palabra «equilátero» proviene del latín y significa literalmente «lados iguales».

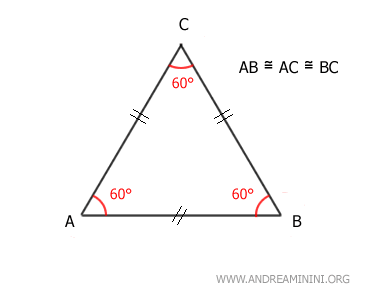
Otra propiedad fundamental de los triángulos equiláteros es que poseen todos sus ángulos iguales, midiendo cada uno 60°. En cualquier triángulo, la suma de los ángulos internos es 180°, lo que equivale a 60° + 60° + 60° en este caso.

Fórmulas

Las principales fórmulas para calcular las propiedades de un triángulo equilátero son:

• Perímetro
  Basta con multiplicar la longitud de uno de sus lados por tres. $$ P = 3 l $$
• Área
  Al igual que en cualquier triángulo, el área se obtiene multiplicando la base (b) por la altura (h) y dividiendo el resultado entre dos. $$ A = \frac{b \cdot h}{2} $$ Para los triángulos equiláteros, también se puede usar esta fórmula específica: $$ A = \frac{l^2 \cdot \sqrt{3}}{4} $$
• Longitud del lado
  Si conoces la altura (h) de un triángulo equilátero, puedes calcular la longitud del lado mediante la siguiente fórmula (demostración): $$ l = \frac{2h}{\sqrt{3}} $$ Otra forma de determinar la longitud del lado es multiplicar el radio (r) de la circunferencia circunscrita por la raíz cuadrada de tres (ver demostración): $$ l = r \cdot \sqrt{3} $$ También es posible calcular la longitud del lado a partir del radio de la circunferencia inscrita (demostración): $$ l = 2r \sqrt{3} $$
• Altura
  La altura se obtiene a partir de la longitud del lado (demostración) mediante la siguiente expresión: $$ h = \frac{l}{2} \sqrt{3} $$

Nota: El hecho de que todos los lados de un triángulo equilátero sean iguales permite calcular tanto el área como el perímetro utilizando fórmulas alternativas, aplicando el Teorema de Pitágoras sobre la mitad del triángulo.

Cómo dibujar un triángulo equilátero

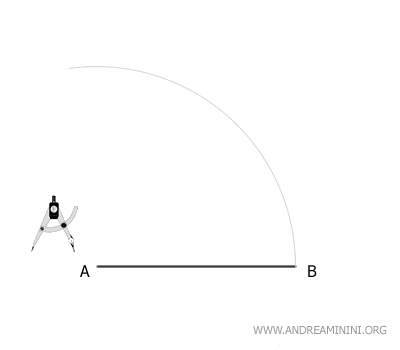
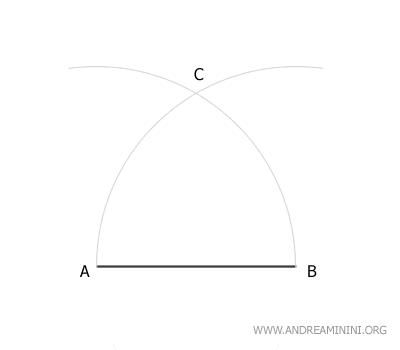
Para trazar un triángulo equilátero, comienza dibujando un segmento de recta AB.

A continuación, coloca la punta del compás en el punto A y dibuja un arco con radio igual a AB.

Sin variar la apertura del compás (radio AB), apóyalo ahora en el punto B y traza un segundo arco.

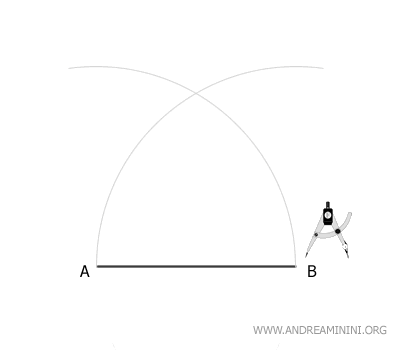
Los dos arcos se cruzan en un punto llamado C.

Ese punto es el tercer vértice del triángulo equilátero.

Une los puntos A y C, y B y C, con segmentos de recta.

El resultado final es un triángulo equilátero.

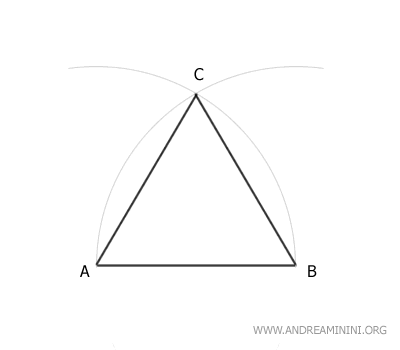
Todos sus lados son iguales, es decir, tienen la misma medida.

Si quieres aprender más técnicas para construir un triángulo equilátero, haz clic aquí.

Curiosidades sobre los triángulos equiláteros

Los triángulos equiláteros presentan las siguientes particularidades:

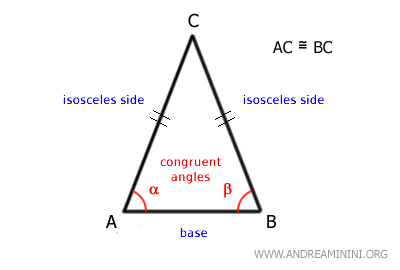
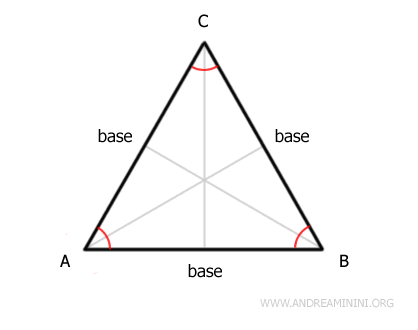
• Un triángulo equilátero es un caso especial de triángulo isósceles con tres bases iguales
  Un triángulo se considera isósceles si tiene dos lados congruentes (AC≅BC). El lado restante (AB) se denomina base y presenta dos ángulos congruentes (α≅β).
  
  En un triángulo equilátero, los tres lados son congruentes (AC≅BC≅AB). Por tanto, cualquiera de sus lados puede considerarse la base, y los otros dos conforman un triángulo isósceles.
  
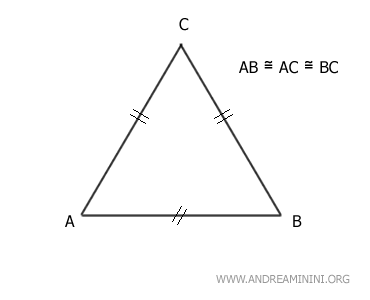
  De este modo, los triángulos equiláteros forman parte del conjunto de triángulos isósceles, en los que la base es congruente con los otros dos lados.

  Esto resulta muy relevante, ya que nos permite aplicar los mismos teoremas tanto a los triángulos isósceles como a los equiláteros para demostrar distintas propiedades.

• Todos los ángulos de un triángulo equilátero son congruentes
  En un triángulo equilátero, sus tres ángulos internos miden lo mismo.
  

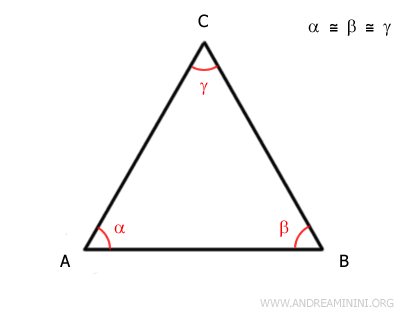
  Demostración. Un triángulo equilátero puede interpretarse como un triángulo isósceles con tres bases. En un triángulo isósceles, los ángulos opuestos a los lados congruentes son iguales (teorema del triángulo isósceles).
  
  En un triángulo equilátero, existen tres posibles bases.
  
  Dado que los ángulos en la base son congruentes, se tiene que $$ \alpha = \beta $$ $$ \beta = \gamma $$ $$ \alpha = \gamma $$ Por la propiedad transitiva, concluimos que $$ \alpha = \beta = \gamma $$ Por lo tanto, todos los ángulos de un triángulo equilátero son congruentes.

• Los ángulos de un triángulo equilátero miden 60°
  En un triángulo equilátero, cada ángulo interno mide exactamente 60 grados.
  

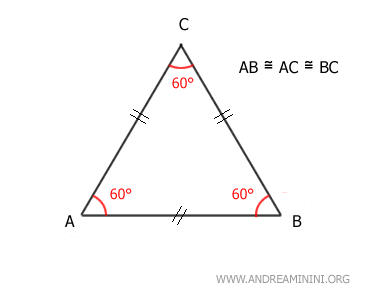
  Demostración. La suma de los ángulos interiores de cualquier triángulo es siempre 180°. Dado que en el triángulo equilátero los tres ángulos son iguales, basta dividir 180° entre tres: $$ 180° \ : \ 3 = 60° $$

• En un triángulo equilátero, cada bisectriz es también mediana y altura
  Las alturas, las medianas, las bisectrices de ángulo y las mediatrices trazadas desde cualquier vértice hacia el lado opuesto coinciden en el mismo segmento, conocido como el eje del triángulo.
  
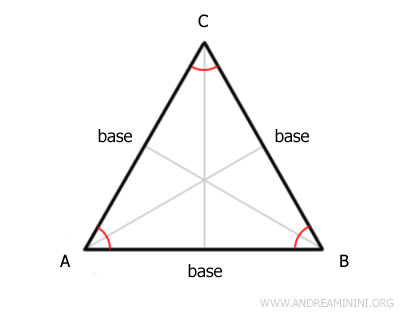
  Por ello, en un triángulo equilátero, el baricentro coincide con el incentro, el circuncentro y el ortocentro.

  Demostración. El triángulo equilátero puede considerarse un caso particular de triángulo isósceles con tres bases iguales. Por lo tanto, los teoremas que se aplican a los triángulos isósceles también son válidos en los equiláteros. En particular, recordemos que en un triángulo isósceles, la bisectriz del ángulo es, a la vez, altura y mediana respecto a la base.
  
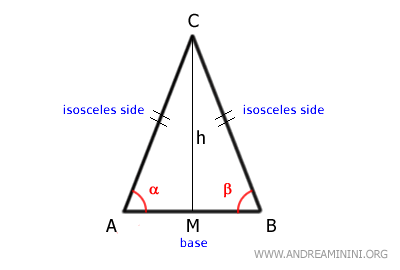
  En el caso del triángulo equilátero, existen tres bases, por lo que todas las bisectrices son simultáneamente alturas y medianas correspondientes a sus lados.
  

• Cada ángulo de un triángulo equilátero representa un tercio de un ángulo llano

  Demostración. Según el teorema de la suma de los ángulos interiores, la suma de los ángulos de un triángulo equivale a un ángulo llano (180°): $$ \alpha + \beta + \gamma = 180° $$ Sabiendo que en el triángulo equilátero los tres ángulos son congruentes, se deduce que cada uno mide la tercera parte de 180°: $$ \alpha = \beta = \gamma = \frac{180°}{3} = 60° $$

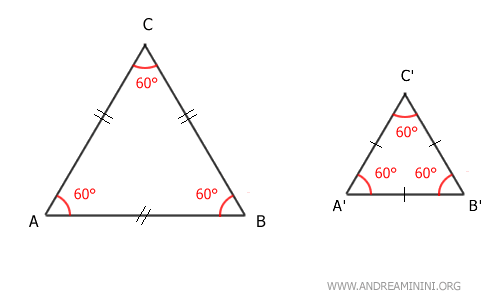
• Cualquier par de triángulos equiláteros son semejantes
  Dos triángulos equiláteros, aunque tengan diferentes dimensiones, poseen siempre ángulos correspondientes iguales. En consecuencia, según el primer criterio de semejanza de triángulos, cualquier par de triángulos equiláteros son semejantes.
  
• En un triángulo equilátero, no es posible trazar la recta de Euler, ya que el baricentro, el circuncentro y el ortocentro coinciden en un mismo punto y, por lo tanto, no son colineales. En su lugar, existen infinitas rectas que pasan por dicho punto.
• El área de un triángulo equilátero puede calcularse mediante la siguiente fórmula:
  $$ A = \frac{l^2 \cdot \sqrt{3}}{4} $$ donde \(l\) representa la longitud de uno de sus lados.
• El lado de un triángulo equilátero equivale al radio de su circunferencia circunscrita multiplicado por √3 $$ l = r \cdot \sqrt{3} $$

  El radio de la circunferencia circunscrita que pasa por los tres vértices del triángulo se calcula como \( l / \sqrt{3} \), siendo \( l \) la longitud de uno de sus lados. $$ r = \frac{l}{\sqrt{3}} $$
  
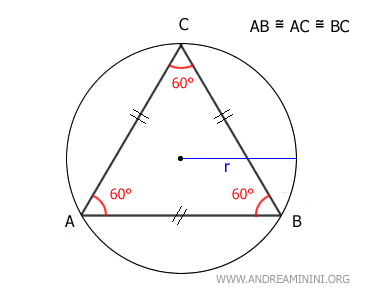
  Por lo tanto, el lado de un triángulo equilátero es igual al radio de la circunferencia circunscrita multiplicado por √3: $$ l = r \cdot \sqrt{3} $$

• El radio de la circunferencia inscrita, tangente a los tres lados del triángulo, se determina como \( l / (2 \cdot \sqrt{3}) \), siendo \( l \) la longitud del lado. $$ r = \frac{l}{2 \cdot \sqrt{3}} $$ En consecuencia, también se puede calcular la longitud del lado del triángulo equilátero a partir del radio de la circunferencia inscrita: $$ l = 2 \sqrt{3} \cdot r $$
  
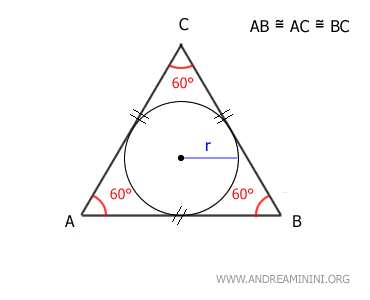
• Relación entre las circunferencias inscrita y circunscrita
  En el triángulo equilátero existe una relación constante entre el radio de la circunferencia inscrita (denotado \(r\)) y el radio de la circunferencia circunscrita (denotado \(R\)). Esta relación se expresa mediante la fórmula: $$ r = \frac{1}{2} \cdot R $$ Esto se debe a que, en un triángulo equilátero, todos los puntos notables (baricentro, ortocentro, circuncentro e incentro) coinciden en un único punto \(O\).
  
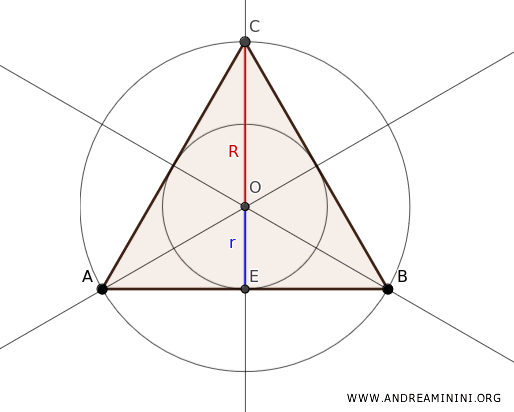
  En particular, el circuncentro y el incentro se superponen, lo que significa que las circunferencias inscrita y circunscrita comparten el mismo centro, aunque poseen radios distintos. Como el baricentro divide cada mediana (por ejemplo, EC) en dos segmentos, uno de los cuales es el doble del otro, se deduce que el radio de la circunferencia circunscrita \(R\) es el doble que el radio de la circunferencia inscrita \(r\), es decir: $$ R = 2r $$ La altura del triángulo equilátero \(ABC\) puede expresarse como la suma de ambos radios: $$ h = r + R $$ Sustituyendo \( R = 2r \) en la ecuación, se obtiene: $$ h = r + 2r = 3r $$ Dado que \( h = r + R \) y \( h = 3r \), se concluye que: $$ 3r = r + R $$ Simplificando, resulta: $$ 2r = R $$, lo que confirma que $$ r = \frac{1}{2}R $$.

Estas propiedades se cumplen exclusivamente en los triángulos equiláteros.

Y así sucesivamente.