Relación entre el lado de un triángulo equilátero y el radio de su circunferencia circunscrita
La longitud del lado de un triángulo equilátero equivale al radio de su circunferencia circunscrita multiplicado por la raíz cuadrada de tres. $$ l = r \cdot \sqrt{3} $$
Un ejemplo práctico
Consideremos el triángulo equilátero ABC y la circunferencia circunscrita que lo contiene, cuyo centro es O y radio \( r \).
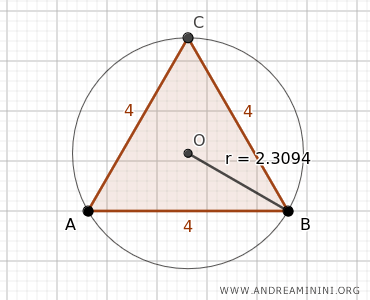
En este caso, el radio de la circunferencia circunscrita es \( r = 2.3094 \).
Podemos aplicar la fórmula para calcular la longitud de un lado del triángulo equilátero:
$$ l = r \cdot \sqrt{3} $$
$$ l = 2.3094 \cdot \sqrt{3} = 4 $$
Este resultado nos indica la longitud de cada lado del triángulo equilátero.
Demostración
Para demostrar esta relación, vamos a analizar un hexágono regular inscrito en una circunferencia de centro O y radio \( r \).
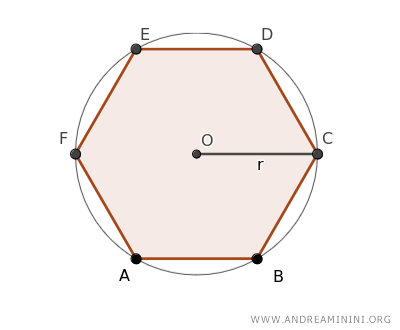
Seleccionamos tres vértices no consecutivos del hexágono - por ejemplo, A, E y C - y los unimos, formando así el triángulo central AEC, junto a tres triángulos periféricos (ABC, AEF y CDE).
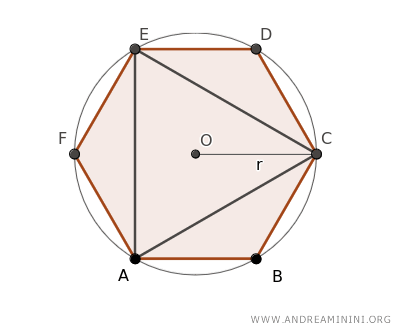
Los triángulos periféricos son congruentes por el primer teorema de congruencia de triángulos, ya que sus lados corresponden a las aristas del hexágono y el ángulo comprendido entre ellos mide 120°.
Por lo tanto, todos sus lados tienen la misma longitud.
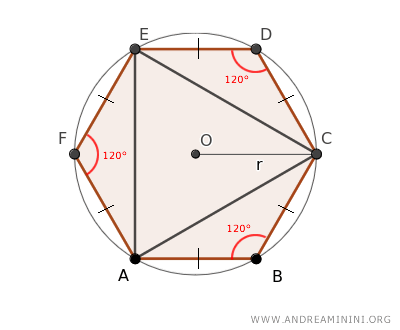
Nota: Un hexágono regular posee todos sus lados iguales y cada uno de sus ángulos interiores mide 120°.
En consecuencia, el triángulo central AEC resulta ser un triángulo equilátero.
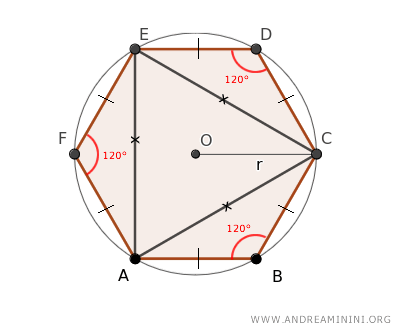
Queremos ahora determinar la longitud de cualquiera de los lados de este triángulo equilátero.
Para ello, trazamos el segmento CF, que coincide con el diámetro de la circunferencia. Así, \( d = 2r \).
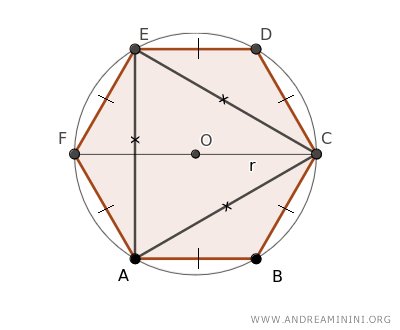
Observando la figura, identificamos otro triángulo, ECF, que comparte el lado EC con el triángulo equilátero AEC.
El ángulo en el vértice E del triángulo ECF es recto, ya que se trata de un ángulo inscrito en una semicircunferencia.
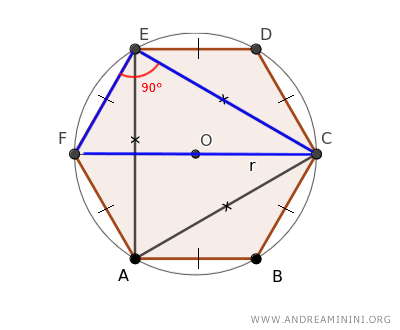
Esto significa que el triángulo ECF es un triángulo rectángulo, lo que nos permite aplicar el teorema de Pitágoras para hallar la longitud del lado EC:
$$ \overline{EC} = \sqrt{ \overline{FC}^2 - \overline{EF}^2 } $$
Sabemos que el segmento FC es el diámetro de la circunferencia, por lo que \( d = 2r \):
$$ \overline{EC} = \sqrt{ (2r)^2 - \overline{EF}^2 } $$
El segmento EF corresponde a uno de los lados del hexágono regular.
Dado que cada lado de un hexágono regular es igual al radio de su circunferencia circunscrita, sustituimos EF = r:
$$ \overline{EC} = \sqrt{ (2r)^2 - r^2 } $$
Procedemos a simplificar paso a paso:
$$ \overline{EC} = \sqrt{ 4r^2 - r^2 } $$
$$ \overline{EC} = \sqrt{ 3r^2 } $$
$$ \overline{EC} = r \sqrt{ 3 } $$
El segmento EC constituye uno de los lados del triángulo equilátero AEC y, por tanto, es congruente con los otros dos lados del triángulo.
Así queda demostrado que el lado de un triángulo equilátero equivale al radio de su circunferencia circunscrita multiplicado por la raíz cuadrada de tres.
Y así sucesivamente.