Bisectrices Perpendiculares de un Triángulo
Una bisectriz perpendicular de un triángulo es una recta que pasa por el punto medio de uno de sus lados y es perpendicular a dicho lado.
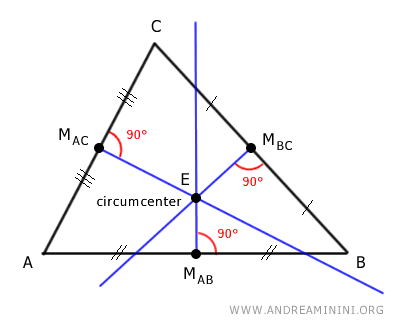
En todo triángulo existen tres bisectrices perpendiculares, una correspondiente a cada lado. Estas rectas también se conocen como mediatrices.
Una bisectriz perpendicular es aquella recta que atraviesa el punto medio de un lado del triángulo (MAB, MBC, MAC), dividiéndolo en dos partes iguales y formando un ángulo recto de 90° con dicho lado.
Cada triángulo posee tres bisectrices perpendiculares, una por cada lado.
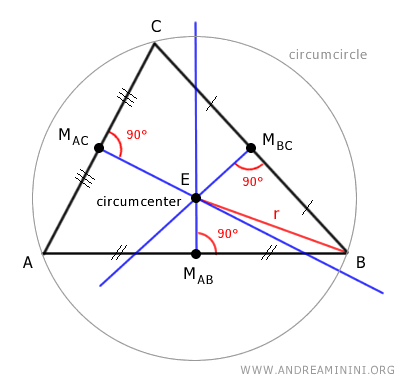
Estas tres bisectrices perpendiculares se intersectan en un único punto denominado circuncentro (E) del triángulo.
El circuncentro (E) es el centro de la circunferencia circunscrita, conocida como la circunferencia circunscrita, que pasa por los tres vértices (A, B y C) del triángulo.
Y así sucesivamente.