Teorema de la Desigualdad Triangular
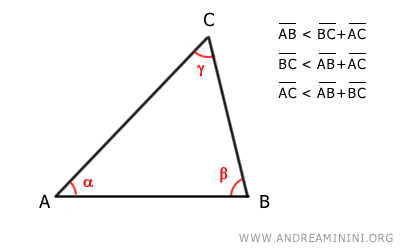
En cualquier triángulo, cada lado es menor que la suma de los otros dos.
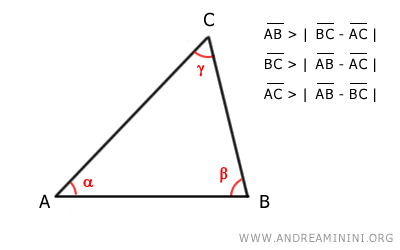
Además, cada lado es mayor que la diferencia entre los otros dos.
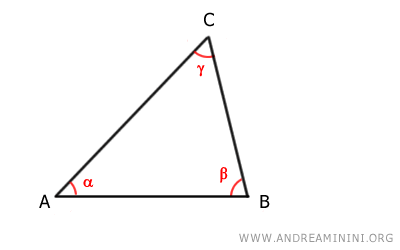
Por ejemplo, consideremos el triángulo ABC.
El lado AB es menor que la suma de los lados BC y AC.
$$ \overline{AB} < \overline{BC}+\overline{AC} $$
La misma relación se cumple para los otros dos lados:
$$ \overline{BC} < \overline{AB}+\overline{AC} $$
$$ \overline{AC} < \overline{AB}+\overline{BC} $$
Este teorema también puede expresarse de forma equivalente: "En un triángulo, cada lado es mayor que la diferencia entre los otros dos lados".
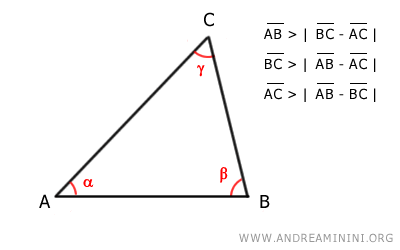
Por ejemplo, si sabemos que AB < BC + AC, $$ \overline{AB} < \overline{BC}+\overline{AC} $$ al restar AC a ambos lados obtenemos AB - AC < BC, $$ \overline{AB} - \overline{AC} < \overline{BC} $$ y de manera análoga para los demás lados.
Un Ejemplo Práctico
Veamos el triángulo ABC:
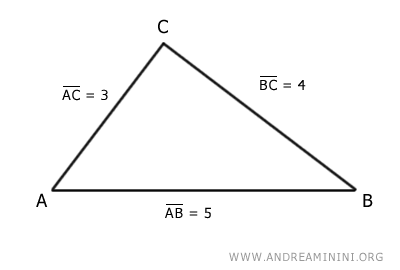
Sus lados miden:
$$ \overline{AB} = 5 $$
$$ \overline{BC} = 4 $$
$$ \overline{AC} = 3 $$
El lado AB, que mide 5 unidades, es menor que la suma de los otros dos lados, AC y BC:
$$ 5 < 4 + 3 = 7 $$
Además, el lado AB es mayor que la diferencia entre AC y BC:
$$ 5 > 4 - 3 = 1 $$
El lado BC, de 4 unidades, es menor que la suma de AB y AC:
$$ 4 < 5 + 3 = 8 $$
Y también es mayor que la diferencia entre AB y AC:
$$ 4 > 5 - 3 = 2 $$
El lado AC, de 3 unidades, es menor que la suma de AB y BC:
$$ 3 < 5 + 4 = 9 $$
Y también es mayor que la diferencia entre AB y BC:
$$ 3 > 5 - 4 = 1 $$
Por tanto, se cumplen todas las condiciones del teorema de la desigualdad triangular.
Demostración
Consideremos un triángulo ABC, donde el lado más largo es AC.
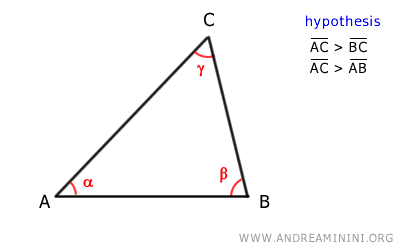
Partimos de estas hipótesis:
$$ \overline{AC} > \overline{BC} $$
$$ \overline{AC} > \overline{AB} $$
Queremos demostrar que el lado AC es menor que la suma de los otros dos:
$$ \overline{AC} < \overline{BC} + \overline{AB} $$
Y también que el lado BC es mayor que la diferencia entre los otros dos lados:
$$ \overline{AC} - \overline{AB} < \overline{BC} $$
Prolongamos el lado AB añadiendo un segmento BD, congruente con BC:
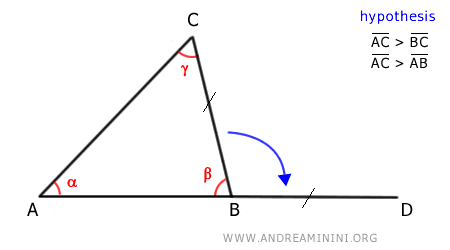
Luego trazamos el segmento CD, que une los puntos C y D:
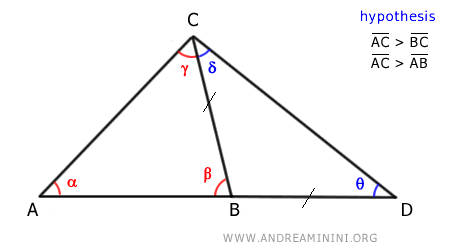
El triángulo BDC es un triángulo isósceles, ya que tiene dos lados de igual longitud.
En un triángulo isósceles, los ángulos opuestos a los lados congruentes también son iguales (δ≅θ):
$$ \delta \cong θ $$
Se observa de inmediato que el ángulo γ + δ es mayor que δ:
$$ \gamma + \delta > \delta $$
Y como δ y θ son iguales, se deduce que γ + δ es también mayor que θ:
$$ \gamma + \delta > θ $$
Consideremos ahora el triángulo ADC:
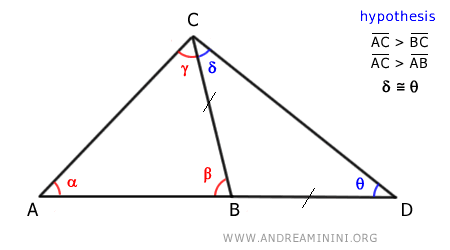
Según el teorema del ángulo mayor, en el triángulo ADC, el lado AC, que se opone al ángulo θ, es menor que el lado AD, opuesto al ángulo γ + δ:
$$ \overline{AC} < \overline{AD} $$
Sabemos que el lado AD equivale a la suma de los segmentos AB y BD:
$$ \overline{AC} < \overline{AB} + \overline{BD} $$
Y dado que BC y BD son congruentes (BC ≅ BD):
$$ \overline{AC} < \overline{AB} + \overline{BC} $$
Hemos probado así que el lado AC es menor que la suma de los lados AB y BC en el triángulo ABC.
Ahora aplicamos la propiedad de la igualdad y restamos AB en ambos lados de la desigualdad:
$$ \overline{AC} - \overline{AB} < \overline{AB} + \overline{BC} - \overline{AB} $$
$$ \overline{AC} - \overline{AB} < \overline{BC} $$
Con esto, también hemos demostrado que el lado BC es mayor que la diferencia entre los otros dos lados del triángulo ABC.
Distancia Entre Tres Puntos en el Espacio
De forma más general, el teorema de la desigualdad triangular sustenta otro resultado fundamental sobre distancias.
En un espacio métrico, dados tres puntos A, B y C, la distancia entre dos puntos cualesquiera d(A,B) es menor o igual que la suma de las distancias entre los otros dos, es decir: $$ d(A,B) \le d(B,C) + d(A,C) $$
En este caso, es importante tener en cuenta que puede darse la igualdad, la cual ocurre cuando los puntos A, B y C están alineados.
Observaciones
Algunas observaciones sobre el teorema de la desigualdad triangular:
- Dadas tres longitudes a, b y c, es posible construir un triángulo con esos segmentos únicamente si cada uno es menor que la suma de los otros dos: $$ a < b+c $$ $$ b < a+c $$ $$ c < a+b $$
Y así sucesivamente.