Teorema del Punto Medio en un Triángulo

En un triángulo, el segmento que une los puntos medios de dos de sus lados es paralelo al tercer lado y mide la mitad de su longitud.

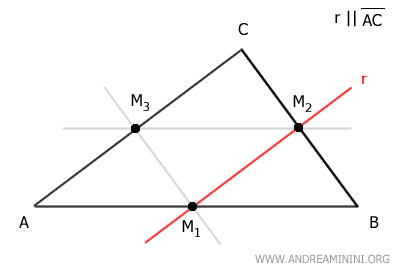
En otras palabras, si trazamos una recta que une los puntos medios de dos lados de un triángulo, esta será paralela al tercer lado y tendrá la mitad de su longitud.

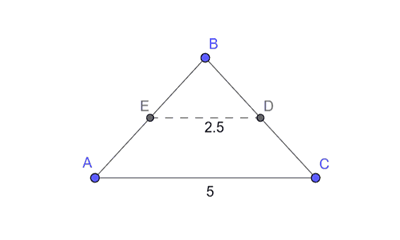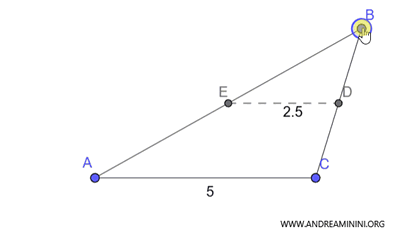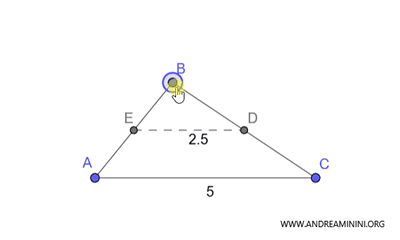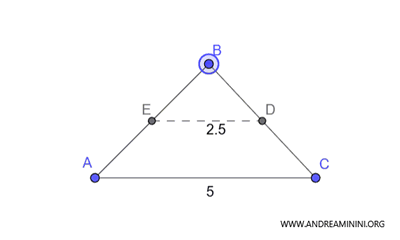
Esta propiedad se cumple en cualquier tipo de triángulo.

Ejemplo

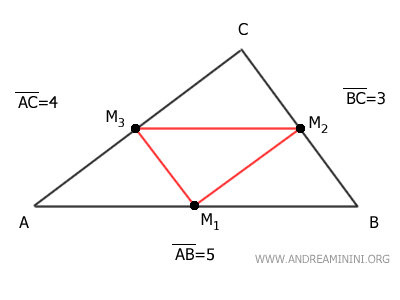
Consideremos el triángulo ABC con las siguientes longitudes de lados: AB=5, BC=3 y AC=4.

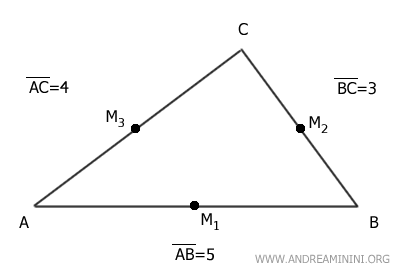
Cada lado posee su punto medio, dividiéndolo en dos segmentos iguales: M₁ en el lado AB, M₂ en el lado BC y M₃ en el lado AC.

Ahora tracemos el segmento que conecta el punto medio M₂ del lado BC con el punto medio M₃ del lado AC.

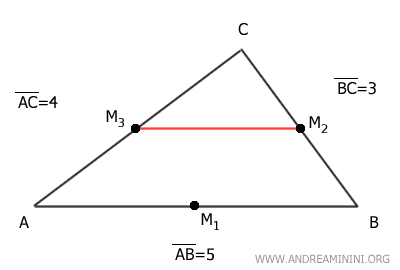
Dicho segmento M₂M₃ es paralelo al lado AB del triángulo.

Además, la longitud de M₂M₃ es la mitad de la longitud del lado AB, es decir, 2.5.

$$ \overline{M_2M_3} = \frac{\overline{AB}}{2} = \frac{5}{2} = 2.5 $$

De forma análoga, el segmento que une los puntos medios M₁ y M₃ es paralelo al lado BC y mide la mitad de su longitud, es decir, 1.5.

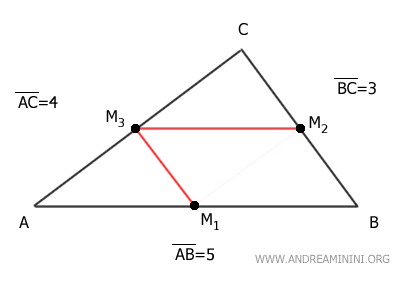
Finalmente, el segmento que conecta los puntos medios M₁ del lado AB y M₂ del lado BC es paralelo al lado AC y mide la mitad de su longitud, es decir, 2.

Corolario

Una recta que pasa por el punto medio M de un lado de un triángulo y es paralela a otro lado, atraviesa también el punto medio del lado restante.

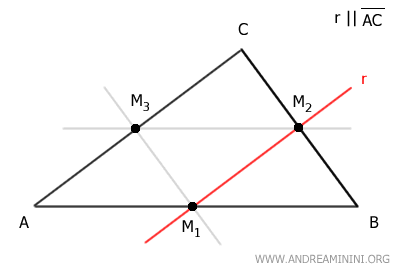
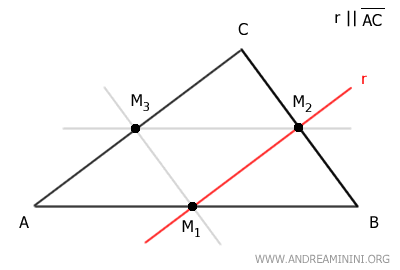
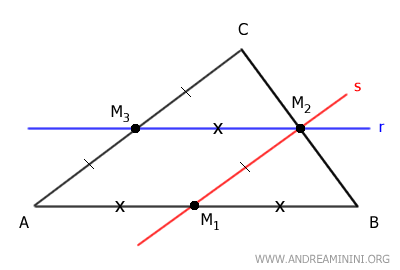
Por ejemplo, tracemos la recta r, paralela al lado AB, que pasa por el punto medio M₂ del lado BC.

Dicha recta atraviesa también el punto medio M₃ del lado AC.

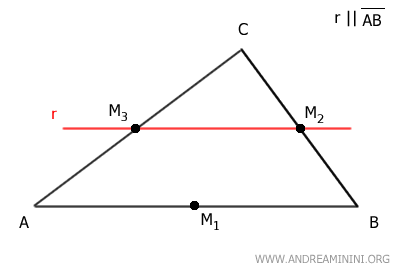
Esta relación es recíproca. Si trazamos una recta r paralela a AB y que pase por el punto medio M₃, también atravesará el punto medio M₂ del lado BC.

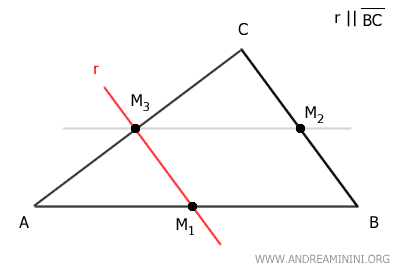
Del mismo modo, si trazamos una recta paralela al lado BC que pase por el punto medio M₃ del lado AC, esta pasará también por el punto medio M₁ del lado AB, y viceversa.

Por último, si trazamos una recta paralela al lado AC que pase por el punto medio M₁ del lado AB, atravesará también el punto medio M₂ del lado BC, y viceversa.

Demostración

Consideremos un triángulo ABC y el punto M sobre el lado AC.

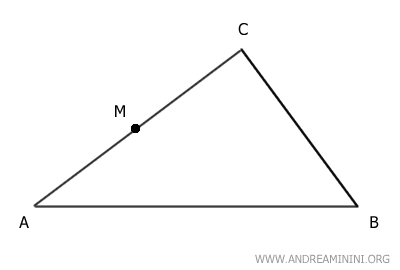
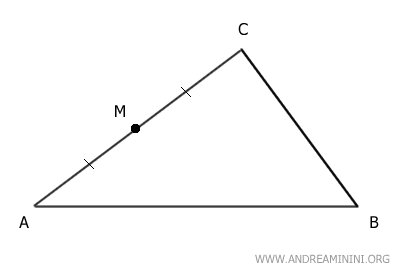
El punto M es el punto medio del lado AC, dividiéndolo en dos segmentos congruentes: AM ≅ CM.

La demostración se divide en tres partes:

A] Si una recta es paralela a un lado y pasa por el punto medio de otro lado, también atraviesa el punto medio del lado restante.

Tracemos dos rectas, r y s, paralelas al lado AB y que pasan, respectivamente, por los puntos M y C.

La recta r corta al lado BC en el punto D.

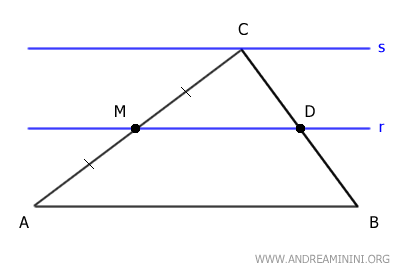
Consideremos el lado AC y las rectas r y s como un conjunto de rectas paralelas, y los lados AC y BC como dos transversales.

Según el teorema de las rectas paralelas, los segmentos correspondientes sobre las transversales son proporcionales.

Así, si AM ≅ CM, entonces BD ≅ CD.

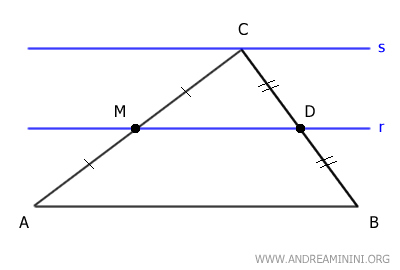
Los segmentos BD y CD resultan congruentes, por lo que el punto D es el punto medio del lado BC.

Esto demuestra que una recta paralela a un lado de un triángulo que pasa por el punto medio de otro lado atraviesa también el punto medio del lado restante.

En conclusión, si un segmento es paralelo a un lado del triángulo y parte del punto medio de otro lado, termina en el punto medio del tercer lado.

B] Si una recta pasa por los puntos medios de dos lados, entonces es paralela al tercer lado del triángulo.

Demostremos ahora la proposición recíproca: si una recta pasa por los puntos medios de dos lados, es paralela al tercer lado del triángulo.

Consideremos el triángulo ABC y una recta r que pasa por los puntos medios M₂ del lado BC y M₃ del lado AC.

Queremos demostrar que la recta r es paralela al lado AB.

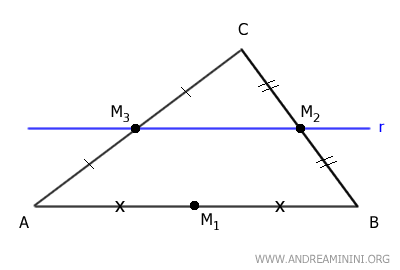
Para ello, recurriremos a una demostración por contradicción.

Supongamos que la recta r pasa por los puntos medios de los lados BC y AC, pero no es paralela al lado AB.

Si esto fuera cierto, según el teorema de las rectas paralelas, debería existir otra recta s paralela a AB, de manera que:

$$ \overline{AM_2} : \overline{CM_2} = \overline{BM_2} : \overline{CM_2} $$

Dado que AM₂ ≡ CM₂, esto implicaría que la recta s cortaría el lado BC en otro punto medio M'₂, diferente de M₂.

Así, el lado BC tendría dos puntos medios: uno, el original M₂, y otro, el construido M'₂.

Como esto es imposible, concluimos que la hipótesis es falsa.

Por lo tanto, es cierto que si una recta pasa por los puntos medios de dos lados de un triángulo, es paralela al tercer lado.

C] El segmento que une dos puntos medios mide la mitad del lado paralelo del triángulo.

En esta última parte de la demostración, debemos probar que el segmento que une dos puntos medios es exactamente la mitad del lado paralelo restante.

Por ejemplo, ya hemos demostrado que el segmento que une los puntos medios M₂ y M₃ es paralelo al lado AB del triángulo.

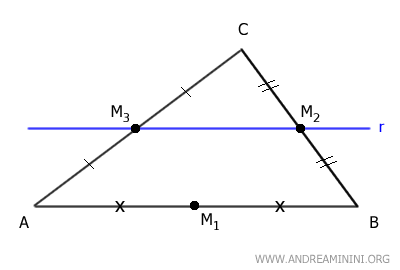
Tracemos una recta s paralela al lado AC que pase por el punto medio M₂.

Dado que esta recta pasa por M₂ y es paralela al lado AC, según el teorema demostrado previamente, esta recta también debe pasar por el punto medio del lado restante, es decir, por el punto medio M₁ del lado AB.

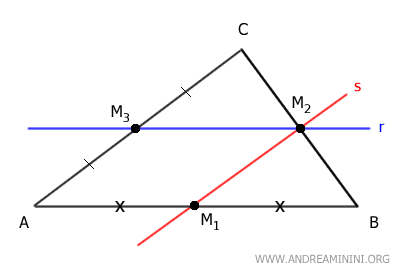
En este momento, el cuadrilátero AM₁M₂M₃ es un paralelogramo, por lo que presenta lados opuestos congruentes y paralelos.

$$ AM_1 \cong M_2 M_3 $$

$$ AM_3 \cong M_1 M_2 $$

De esto se deduce que el segmento M₂M₃ es congruente al segmento AM₁, que equivale a la mitad de la longitud del lado AB.

$$ AM_3 \cong \frac{\overline{AB}}{2} $$

Esto demuestra que la distancia entre los puntos medios de dos lados de un triángulo es exactamente la mitad de la longitud del lado restante.

Y así sucesivamente.