Criterios de semejanza de triángulos

Los criterios de semejanza de triángulos establecen las condiciones fundamentales que permiten determinar cuándo dos triángulos son semejantes.

Estos criterios son sumamente útiles, ya que permiten verificar la semejanza entre dos triángulos sin necesidad de analizar en detalle todos sus elementos.

Existen tres criterios principales para determinar la semejanza de triángulos.

Criterio de semejanza por Ángulo-Ángulo-Ángulo (AAA)

Dos triángulos son semejantes si tienen dos ángulos correspondientes congruentes.

Cuando dos triángulos poseen dos ángulos internos iguales y dispuestos en el mismo orden, esto garantiza que el tercer ángulo también será congruente.

De este modo, ambos triángulos conservan la misma forma en el plano, aunque sus dimensiones puedan variar.

Este criterio se conoce también como el criterio de semejanza AAA.

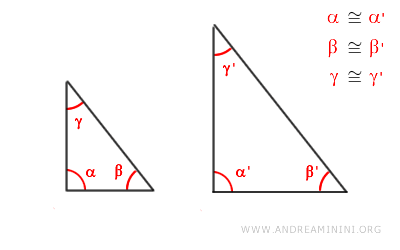
Por ejemplo, si dos triángulos presentan dos ángulos correspondientes congruentes α≅α' y β≅β',

$$ \alpha \cong \alpha ' $$

$$ \beta \cong \beta ' $$

cumplen con el criterio de semejanza y, por lo tanto, son semejantes.

Nota: Basta comprobar que dos pares de ángulos correspondientes sean congruentes en un triángulo, puesto que la suma de los ángulos internos siempre es 180°. Por ello, si dos triángulos tienen dos ángulos iguales α y β, el tercero coincide necesariamente, ya que es el complemento hasta 180°, es decir, γ≅180°-α-β. Este principio se cumple para cualquier par de ángulos internos correspondientes.

Criterio de semejanza por Lado-Ángulo-Lado (LAL)

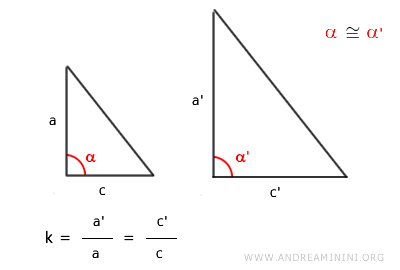
Dos triángulos son semejantes si tienen dos lados correspondientes proporcionales y el ángulo comprendido entre ellos es congruente.

Si dos triángulos presentan lados correspondientes en la misma proporción \( k \), y el ángulo incluido entre dichos lados es congruente, se considera que son semejantes.

Este criterio recibe también el nombre de criterio de semejanza LAL.

Criterio de semejanza por Lado-Lado-Lado (LLL)

Dos triángulos son semejantes si todos sus lados correspondientes son proporcionales.

Si cada lado de un triángulo guarda la misma proporción con respecto al lado correspondiente del otro triángulo, en razón \( k \), entonces ambos son semejantes.

Este criterio se conoce también como el criterio de semejanza LLL.

 

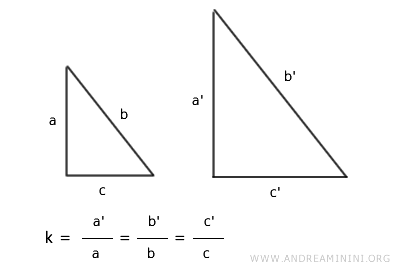
Y, en esencia, esto resume lo fundamental sobre los criterios de semejanza de triángulos.