Semejanza

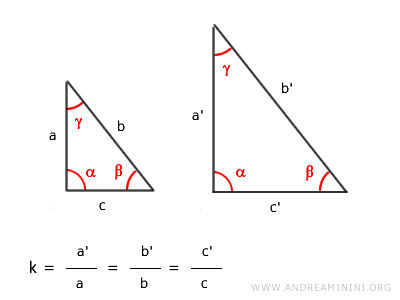
La semejanza es una transformación geométrica que conserva la forma de una figura. Mantiene todos los ángulos correspondientes congruentes y establece una razón constante $ k $ entre los lados correspondientes. Cualquier transformación de este tipo puede obtenerse combinando una homotecia con una isometría.

La transformación que genera esta relación se denomina similitud, y suele representarse con la letra griega sigma en minúscula, $ \sigma $.

Es una transformación geométrica que mantiene la forma de la figura original, aunque su tamaño pueda cambiar.

En otras palabras, dos figuras son semejantes si una puede obtenerse a partir de la otra mediante una similitud. Esto ocurre cuando se cumplen las siguientes condiciones:

1. Los ángulos correspondientes son congruentes
2. Los lados correspondientes son proporcionales, todos con la misma razón $ k $

Por lo tanto, una figura semejante conserva la misma forma, pero con dimensiones distintas.

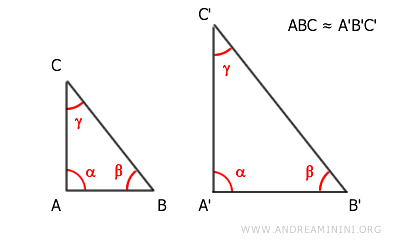
Para expresar que dos figuras son semejantes, se utiliza el símbolo "≈".

Por ejemplo, si los triángulos ABC y A'B'C' son semejantes, escribimos:

$$ ABC ≈ A'B'C' $$

Los elementos que se corresponden en ambas figuras (lados y ángulos) se llaman lados correspondientes y ángulos correspondientes.

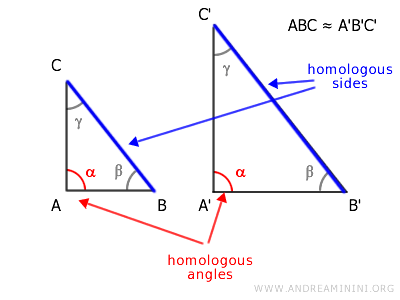
Nota. En los triángulos semejantes, cada lado correspondiente es el que se encuentra frente al mismo ángulo en ambas figuras. En resumen, los lados correspondientes son los que se oponen a ángulos iguales.

La razón de proporcionalidad $ k $ es la misma para todos los lados correspondientes y se denomina razón de semejanza o factor de escala.

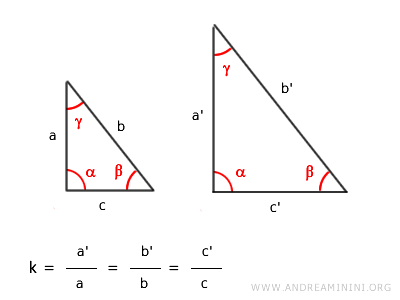
En consecuencia, los invariantes de la semejanza son las medidas de los ángulos y las razones entre los lados correspondientes.

• Conserva las razones de longitud.
• Conserva las medidas de los ángulos, ya que cada uno se transforma en un ángulo congruente.
• Si dos rectas son perpendiculares en la figura original, también lo serán en la semejante. Del mismo modo, si dos rectas son paralelas, seguirán siéndolo.

Como resultado, la semejanza conserva el paralelismo: si dos lados de la figura original son paralelos, sus correspondientes en la figura semejante también lo serán (afinidad).

Un ejemplo cotidiano de semejanza es ampliar una fotografía. La imagen ampliada y la original mantienen exactamente la misma forma, aunque tengan tamaños distintos.

La semejanza también se extiende a la geometría del espacio. Dos sólidos son semejantes si sus ángulos correspondientes son congruentes y sus aristas correspondientes son paralelas, manteniendo la misma razón |k|.

La razón de semejanza

Cuando dos figuras son semejantes, los lados correspondientes guardan una proporción constante. Esta razón se llama razón de semejanza o factor de escala, y siempre es positiva ( $ k > 0 $ ).

• Ampliación (k>1)
  Si la razón de semejanza es mayor que 1, la figura resultante es una ampliación con escala 1:k.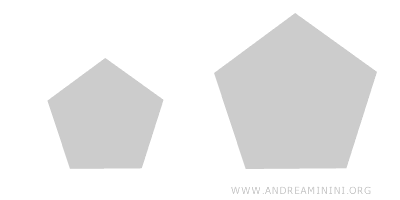

  
  Por ejemplo, si k=2, la figura se amplía al doble. Cada lado de la nueva figura mide el doble que el correspondiente en la original.

• Isometría (k=1)
  Si la razón es igual a 1, la transformación es una isometría, como una rotación, una traslación o una reflexión.
  
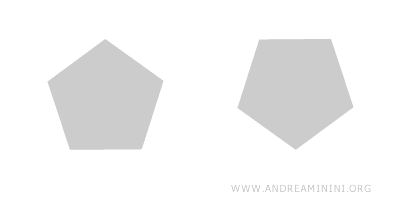
• Reducción (0<k<1)
  Si la razón está entre 0 y 1, la figura es una reducción con escala 1:k.
  

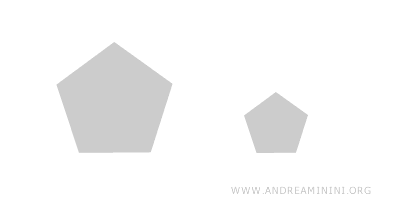
  Por ejemplo, si k=0.5, la figura se reduce a escala 1:0.5, equivalente a una escala 2:1.

En todos los casos, las figuras semejantes conservan siempre la misma forma.

Polígonos Semejantes

Dos polígonos se consideran semejantes si sus lados correspondientes están en una proporción constante y sus ángulos son iguales en medida, garantizando que sus formas sean congruentes.

Por extensión, todos los polígonos regulares y los círculos son, entre sí, figuras semejantes por naturaleza.

Criterios de Semejanza de Triángulos

Existen criterios específicos que determinan la semejanza entre figuras geométricas, especialmente entre triángulos, entre los cuales destacan:

• Criterio AAA (Ángulo-Ángulo-Ángulo)
  Dos triángulos son semejantes si tienen sus ángulos correspondientes congruentes, estableciendo la semejanza únicamente a partir de la igualdad angular.
  

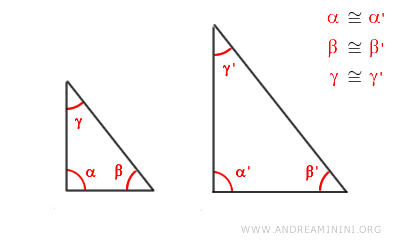
  Nota: En la práctica, basta comprobar que dos ángulos sean congruentes para asegurar la semejanza de dos triángulos, ya que el tercer ángulo será necesariamente igual, dado que la suma de los ángulos interiores de un triángulo es siempre 180 grados.

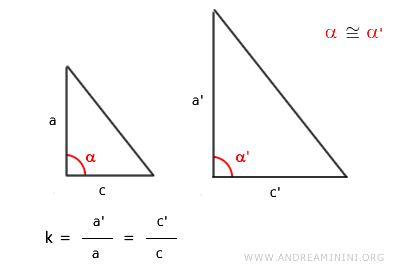
• Criterio LAL (Lado-Ángulo-Lado)
  La semejanza también se establece cuando dos lados de un triángulo son proporcionales a los de otro y el ángulo comprendido entre ellos es congruente.
  
• Criterio LLL (Lado-Lado-Lado)
  Dos triángulos son semejantes si sus tres lados son proporcionales, lo que implica un mismo factor de escala en todos los lados correspondientes.
  

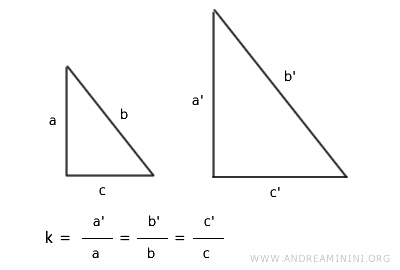
Ecuaciones de la Semejanza

La representación matemática de la semejanza en el plano cartesiano se expresa mediante un sistema de ecuaciones matriciales que refleja cómo la transformación afecta las coordenadas.

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = M \cdot \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} c \\ d \end{pmatrix} $$

La matriz M varía en función de si se trata de una semejanza directa o inversa.

• Semejanza Directa $$ M = \begin{pmatrix} a & -b \\ b &a \end{pmatrix} $$
• Semejanza Inversa $$ M = \begin{pmatrix} a & b \\ b & -a \end{pmatrix} $$

Así, las semejanzas directas e inversas obedecen sistemas cartesianos distintos, y la razón de semejanza k se determina mediante:

$$ k = \sqrt{a^2+b^2} $$

Otra forma de describir la semejanza es a través de expresiones trigonométricas, lo que evidencia la versatilidad de estas transformaciones en la geometría.

Ejemplo

Analicemos una transformación geométrica y sus efectos sobre una figura simple del plano. Estudiaremos cómo actúa, qué tipo de transformación representa y cómo modifica las longitudes y la orientación de un triángulo.

Partimos de la siguiente aplicación:

\[ \tau:\; \begin{cases} x' = 2x + y + 1 \\ \\ y' = x - 2y - 1 \end{cases} \]

Su parte lineal está asociada a la matriz:

\[ A= \begin{pmatrix} 2 & 1\\ 1 & -2 \end{pmatrix} \]

Esta matriz tiene la forma \(\begin{pmatrix} a & b \\ b & -a \end{pmatrix}\), con \(a=2\) y \(b=1\), lo que nos indica que se trata de una similitud inversa. Este tipo de transformación conserva las proporciones y los ángulos, pero invierte la orientación de la figura.

Comprobemos primero el determinante:

\[ \det A = (2)(-2) - (1)(1) = -5 \]

El valor negativo confirma que la orientación se invierte. A continuación, calculamos el factor de escala de la similitud:

\[ k=\sqrt{a^2+b^2}=\sqrt{2^2+1^2}=\sqrt{5} \]

Esto significa que la transformación multiplica todas las longitudes por \(\sqrt{5}\).

Aplicamos ahora \(\tau\) al triángulo rectángulo isósceles \(OAB\), con vértices \(\,O(0,0),\;A(1,0),\;B(0,1)\).

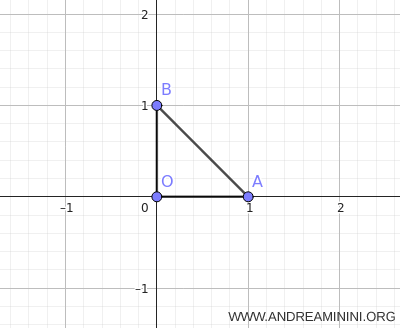
Determinamos las imágenes de los vértices sustituyendo las coordenadas en el sistema:

• Punto \(O\): \(O'(1,-1)\)
• Punto \(A\): \(A'(3,0)\)
• Punto \(B\): \(B'(2,-3)\)

Como referencia, el cálculo para el punto \(O\) es el siguiente:

\[ x' = 2\cdot 0 + 0 + 1 = 1,\qquad y' = 0 - 2\cdot 0 - 1 = -1 \]

El triángulo transformado \(O'A'B'\) queda definido por los puntos \(O'(1,-1)\), \(A'(3,0)\) y \(B'(2,-3)\).

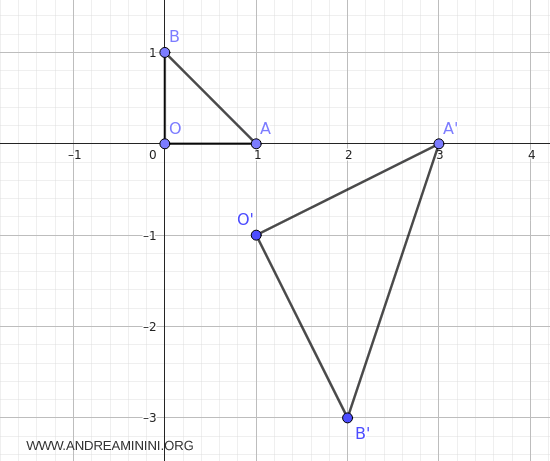
Antes de transformar, las longitudes originales eran:

• \(\overline{OA}=1\)
• \(\overline{OB}=1\)
• \(\overline{AB}=\sqrt{2}\)

Después de aplicar la similitud, las longitudes se multiplican por \(\sqrt{5}\):

• \( O'A' = \sqrt{5}\)
• \( O'B' = \sqrt{5}\)
• \( A'B' = \sqrt{10}\)

La figura resultante conserva sus ángulos y su forma, pero aparece ampliada y con orientación invertida. El triángulo sigue siendo rectángulo e isósceles.

Semejanza Espacial

La semejanza espacial se define de manera análoga a la semejanza en el plano.

Es una transformación geométrica que resulta de la combinación de una isometría (transformación que preserva distancias, como traslaciones, rotaciones o simetrías) con una dilatación (transformación que amplía o reduce un objeto manteniendo sus proporciones).

Principales propiedades de la semejanza espacial

La semejanza espacial presenta las siguientes características:

• Preserva los ángulos entre elementos geométricos.
• Transforma segmentos en otros proporcionales, manteniendo una razón constante de semejanza.
• La razón de semejanza coincide con el factor de dilatación y determina la escala de la transformación.

Ejemplos reales de semejanza espacial

Si una estructura se amplía con una razón de semejanza \( k = 2 \), todas sus dimensiones - longitud, altura y profundidad - se duplican con respecto al objeto original.

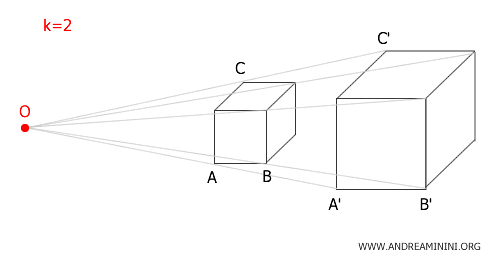
Por el contrario, si un sólido se somete a una transformación con razón de semejanza \( k = \frac{1}{2} \), sus aristas se reducirán a la mitad de su longitud original, aunque su forma permanezca inalterada.

Observaciones

Al profundizar en el concepto de semejanza, surgen varias ideas esenciales que permiten comprender con mayor claridad esta transformación geométrica:

• Una semejanza es la composición de una homotecia y una isometría
  En el plano, toda semejanza puede descomponerse como la combinación de una homotecia y una isometría (traslación, rotación, reflexión axial o central, o incluso la identidad), en cualquier orden. El siguiente ejemplo muestra de manera visual cómo ambas transformaciones actúan conjuntamente para producir una semejanza.
  
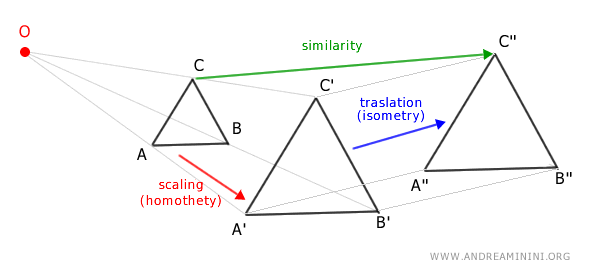
• La composición de dos semejanzas también es una semejanza
  Cuando combinamos dos semejanzas con factores de escala k₁ y k₂, obtenemos otra semejanza cuyo factor de escala es el producto k₁·k₂. Es decir, al aplicar una semejanza tras otra, el resultado sigue siendo una transformación del mismo tipo.
• Isometrías y homotecias: tipos especiales de semejanzas
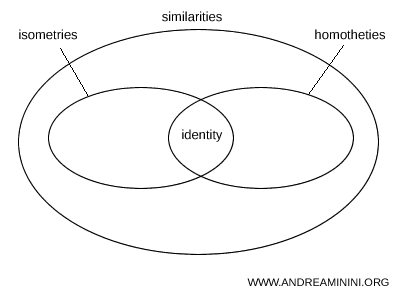
  Dentro del conjunto general de las semejanzas encontramos dos casos muy importantes: las isometrías y las homotecias. Todas ellas son transformaciones que conservan los ángulos y las proporciones entre longitudes, aunque no necesariamente las distancias absolutas.
  • Una isometría es una semejanza con factor de escala unitario $ k = 1 $, lo que significa que todas las distancias permanecen exactamente iguales.
  • Una homotecia es una semejanza con un centro fijo y sin rotación ni traslación, que multiplica las distancias desde ese punto por un mismo factor $ k $.
  Por tanto, todas las isometrías y las homotecias son semejanzas, pero no ocurre lo contrario:
  • No toda semejanza es una isometría, ya que el factor de escala puede ser distinto de uno ( $ k \ne 1 $ ).
  • Tampoco toda semejanza es una homotecia, porque puede incluir rotaciones, traslaciones o simetrías además de la dilatación.
  En resumen, las isometrías y las homotecias son subconjuntos dentro del conjunto más amplio de las semejanzas. Este conjunto general incluye las isometrías cuando $ k = 1 $ y las homotecias cuando no intervienen rotaciones ni traslaciones.
  
• Las figuras congruentes son un caso particular de figuras semejantes
  Toda pareja de figuras congruentes es, necesariamente, semejante. En efecto, una congruencia puede interpretarse como la composición de una homotecia con centro arbitrario y razón 1, seguida de una isometría (identidad, traslación, rotación o reflexión).
• Centro de semejanza
  En el plano, toda semejanza que no sea una traslación posee un punto fijo, es decir, un punto que permanece invariante bajo la transformación. Este punto recibe el nombre de centro de semejanza.
• Semejanzas directas e indirectas
  Una semejanza se denomina directa si conserva la orientación de la figura, e indirecta si la invierte.
• Relación entre los perímetros de dos figuras semejantes
  Si dos figuras planas son semejantes con razón $ k $, entonces sus perímetros guardan la misma proporción $ k $. En particular, si $ F' $ es la imagen de $ F $ mediante una semejanza de razón $ k $, se verifica: $$ \text{Perimeter}(F') = k \cdot \text{Perimeter}(F) $$

  Nota. La semejanza multiplica todas las longitudes por $ k $. Como el perímetro es una magnitud lineal, se escala por el mismo factor. Por ejemplo, si el perímetro de un cuadrado es $ P = 4L $, entonces un cuadrado semejante de lado $ kL $ cumple: $$ P' = 4(kL) = k \cdot (4L) = k \cdot P $$

• Relación entre las áreas de dos figuras semejantes
  Si dos figuras planas son semejantes con razón $ k $, entonces la relación entre sus áreas es $ k^2 $. En particular, si $ F' $ es la imagen de $ F $ mediante una semejanza de razón $ k $, entonces: $$ \text{Area}(F') = k^2 \cdot \text{Area}(F) $$

  Nota. La semejanza multiplica cada longitud por $ k $. Como el área depende de dos dimensiones lineales, el factor total es $ k^2 $. Por ejemplo, si el área de un cuadrado es $ A = L \cdot L $, entonces un cuadrado semejante con lado $ kL $ cumple: $$ A' = (kL) \cdot (kL) = k^2 \cdot (L \cdot L) $$

• Relación entre los volúmenes de dos cuerpos semejantes
  En el espacio tridimensional, si dos sólidos son semejantes con razón \(k\), entonces sus volúmenes guardan la proporción \(k^3\). En particular, si \(F'\) es la imagen de \(F\) bajo una semejanza de razón \(k\), se tiene: \[ \text{Volume}(F') = k^3 \cdot \text{Volume}(F) \]

  Nota. La semejanza multiplica cada dimensión lineal por \(k\). Como el volumen depende de tres dimensiones, el factor acumulado es \(k^3\). Por ejemplo, si un cubo tiene volumen \(V = L \cdot L \cdot L\), entonces un cubo semejante con lado \(kL\) cumple: \[ V' = (kL)\cdot(kL)\cdot(kL) = k^3 \cdot (L \cdot L \cdot L) = k^3 \cdot V \]

Estas observaciones ofrecen una visión más profunda y estructurada de la semejanza, y muestran cómo esta transformación organiza de manera coherente las relaciones geométricas tanto en el plano como en el espacio.