Transformaciones afines

Una transformación afín (o afinidad) es una operación geométrica que conserva la alineación de los puntos y el paralelismo de las rectas, aunque no necesariamente las distancias ni los ángulos.

En otras palabras, una transformación afín puede trasladar, rotar, escalar, reflejar o deformar una figura, siempre que las líneas rectas sigan siendo rectas y las paralelas continúen siéndolo. El orden de los puntos sobre una misma recta nunca se altera.

La alineación y el paralelismo son los dos grandes invariantes de toda transformación afín.

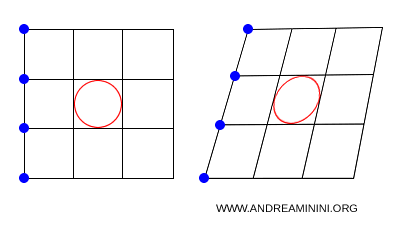
Por lo general, las longitudes, los ángulos y las áreas cambian. Esto significa que la forma global de una figura puede modificarse: un triángulo rectángulo, por ejemplo, puede transformarse en uno acutángulo o en uno obtusángulo.

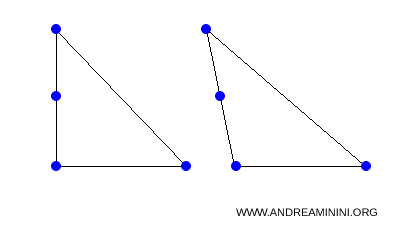
Desde el punto de vista matemático, una transformación afín es una aplicación que relaciona puntos, rectas y figuras de un plano o del espacio con otros, manteniendo el paralelismo entre las rectas.

$$ \mathbf{y} = A\mathbf{x} + \mathbf{b} $$

En esta ecuación, \( \mathbf{x} \) representa las coordenadas iniciales, \( A \) es la matriz que define la parte lineal de la transformación (rotaciones, escalados, reflexiones, etc.), y \( \mathbf{b} \) es el vector de traslación que desplaza la figura completa.

Las transformaciones afines pueden o no ser isometrías. En las isometrías se conservan distancias y ángulos; en las demás, estos cambian. Sin embargo, el paralelismo y la colinealidad siempre permanecen intactos.

Ejemplos prácticos

Ejemplo 1: afinidad no isométrica

Esta transformación es afín porque mantiene el paralelismo de las rectas y la alineación de los puntos. No obstante, no es isométrica, ya que las longitudes y los ángulos se modifican.

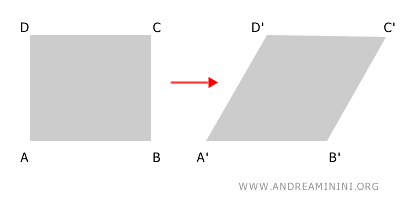
Ejemplo 2: afinidad isométrica

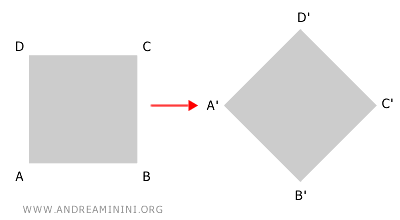
En este caso, la transformación combina una traslación con una rotación. El resultado es una afinidad isométrica que conserva la congruencia de las longitudes y los ángulos, además del paralelismo y la colinealidad.

El cociente de afinidad

En toda transformación afín, la relación entre las áreas de dos figuras correspondientes es constante: $$ \frac{A_{S'}}{A_S} = k $$. Si $ S $ es una figura plana y $ S' $ su imagen afín, la constante \( k \) se conoce como cociente de afinidad.

Cuando $ k = 1 $, las áreas son iguales, lo que significa que la transformación conserva el área.

Las transformaciones que conservan el área reciben el nombre de equiafinidades o afinidades que preservan el área.

Ejemplo

Imaginemos un cuadrado \(S\) de lado 2. Su área es:

\( A_S = 2^2 = 4. \)

Aplicamos una transformación que estira las coordenadas horizontales al doble y deja sin cambios las verticales. Matemáticamente se expresa así:

\[ \begin{cases} x' = 2x \\ \\ y' = y \end{cases} \]

La nueva figura \(S'\) es un rectángulo con base 4 y altura 2, cuya área vale:

\( A_{S'} = 4 \times 2 = 8. \)

De modo que:

\[ \frac{A_{S'}}{A_S} = \frac{8}{4} = 2 = k. \]

El cociente de afinidad es, por tanto, \(k = 2\).

Nota. Si la transformación fuera solo una rotación o una traslación (sin escalado), entonces \(k = 1\) y el área se conservaría. En ese caso, la transformación sería equiafín.

Ecuaciones de la Transformación Afín

En geometría analítica, una transformación afín describe cómo un conjunto de puntos en el plano se transforma mediante una combinación de operaciones lineales y traslaciones. En otras palabras, es una forma general de cambiar de posición, orientación o tamaño una figura geométrica sin perder su estructura esencial.

Se representa mediante el siguiente sistema de ecuaciones lineales:

\[
\begin{cases}
x' = a x + b y + c \\ \\
y' = a' x + b' y + c'
\end{cases}
\]

Los coeficientes \( a, b, a', b' \) determinan la parte lineal de la transformación, que puede incluir rotaciones, dilataciones o cizallamientos. Los términos \( c \) y \( c' \), en cambio, controlan la traslación de la figura en el plano.

Para que la transformación sea válida e invertible, el determinante de la matriz lineal debe ser distinto de cero:

\[ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} \ne 0 \]

Esta condición garantiza que cada punto del plano original tenga una única imagen y que la transformación pueda revertirse. El signo del determinante también nos indica el tipo de transformación:

• Transformación afín directa
  Si el determinante es positivo, la figura conserva su orientación original. \[ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} > 0 \]
  
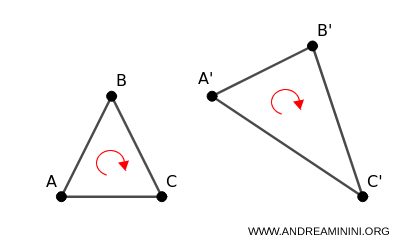
• Transformación afín indirecta
  Si el determinante es negativo, la orientación se invierte, lo que implica que la figura queda reflejada respecto a un eje. \[ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} < 0 \]
  

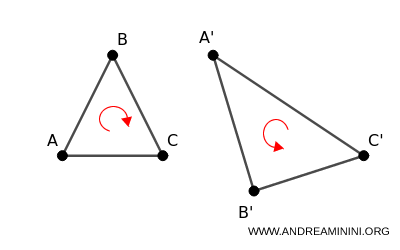
En resumen, una transformación directa mantiene la orientación de la figura, mientras que una indirecta la invierte al mismo tiempo que la deforma o la traslada.

Ejemplo práctico

Supongamos un triángulo con vértices \( A(1, 1), B(2, 3), C(3, 1) \). Aplicamos la siguiente transformación afín:

\[
\begin{cases}
x' = 2x + y + 1 \\ \\
y' = x + y + 2
\end{cases}
\]

El determinante de la parte lineal es:

\[
D =
\begin{vmatrix}
2 & 1 \\
1 & 1
\end{vmatrix}
= 2 \cdot 1 - 1 \cdot 1 = 1 > 0
\]

Como el determinante es positivo, la transformación es directa y conserva la orientación del triángulo original.

Calculemos las imágenes de los vértices:

• A(1, 1): \[ x'_A = 2(1) + 1 + 1 = 4 \] \[ y'_A = 1 + 1 + 2 = 4 \] → \( A′(4, 4) \)
• B(2, 3): \[ x'_B = 2(2) + 3 + 1 = 8 \] \[ y'_B = 2 + 3 + 2 = 7 \] → \( B′(8, 7) \)
• C(3, 1): \[ x'_C = 2(3) + 1 + 1 = 8 \] \[ y'_C = 3 + 1 + 2 = 6 \] → \( C′(8, 6) \)

El triángulo transformado tiene vértices \( A′(4, 4), B′(8, 7), C′(8, 6) \). La figura se ha desplazado y deformado, pero conserva el sentido original de sus vértices porque el determinante es positivo.

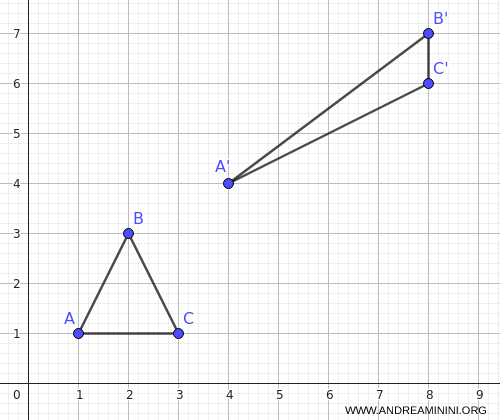
Ejemplo 2: transformación indirecta

Consideremos nuevamente el triángulo \( A(1, 1), B(2, 3), C(3, 1) \), pero esta vez aplicamos una transformación con determinante negativo:

\[
\begin{cases}
x' = x + 2y \\ \\
y' = 3x + y
\end{cases}
\]

El determinante es:

\[
D =
\begin{vmatrix}
1 & 2 \\
3 & 1
\end{vmatrix}
= 1\cdot1 - 3\cdot2 = 1 - 6 = -5 < 0
\]

Al ser negativo, la transformación es indirecta: la figura resultante está reflejada respecto a la original.

Calculamos las imágenes de los vértices:

• A(1, 1): \[ x'_A = 1 + 2(1) = 3 \] \[ y'_A = 3(1) + 1 = 4 \] → \( A′(3, 4) \)
• B(2, 3): \[ x'_B = 2 + 2(3) = 8 \] \[ y'_B = 3(2) + 3 = 9 \] → \( B′(8, 9) \)
• C(3, 1): \[ x'_C = 3 + 2(1) = 5 \] \[ y'_C = 3(3) + 1 = 10 \] → \( C′(5, 10) \)

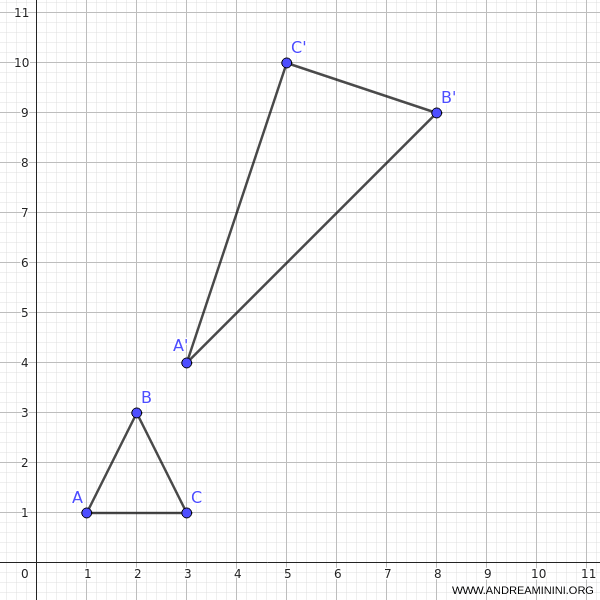
El triángulo transformado tiene vértices \( A′(3, 4), B′(8, 9), C′(5, 10) \). En este caso, la orientación del triángulo se invierte: si en el original los vértices estaban dispuestos en sentido antihorario, en la imagen aparecen en sentido horario.

El signo del determinante, por tanto, no solo nos dice si la transformación es invertible, sino también si mantiene o invierte la orientación geométrica de la figura.

Puntos fijos en las transformaciones afines

En una transformación afín pueden existir uno, ninguno o infinitos puntos fijos. Se llama punto fijo a aquel que no cambia de posición al aplicarse la transformación: su imagen coincide exactamente con él mismo.

Cuando una transformación afín tiene un único punto fijo, se denomina afinidad central o transformación centro-afín.

De manera inmediata se deduce que, si una transformación afín posee dos puntos fijos distintos, en realidad existen infinitos. Esto ocurre porque ambos puntos determinan una recta, y todos los puntos de esa recta permanecen invariantes.

Demostración

La forma general de una transformación afín en el plano puede expresarse así:

\[ \begin{cases} x' = a x + b y + c \\ y' = a' x + b' y + c' \end{cases} \]

Si un punto \( (x', y') \) es fijo, entonces \( x' = x \) y \( y' = y \). Sustituyendo estas igualdades en las ecuaciones anteriores, se obtiene:

\[ \begin{cases} x = a x + b y + c \\ y = a' x + b' y + c' \end{cases} \]

Lo que equivale a:

\[ \begin{cases} (a - 1)x + b y + c = 0 \\ a' x + (b' - 1)y + c' = 0 \end{cases} \]

O, de forma más sencilla,

\[ \begin{cases} (a - 1)x + b y = -c \\ a' x + (b' - 1)y = -c' \end{cases} \]

Este sistema lineal de ecuaciones puede resolverse de tres maneras posibles:

• Compatible determinado: el sistema tiene una única solución, por lo tanto existe un solo punto fijo.
• Incompatible: el sistema no tiene solución, es decir, no hay ningún punto fijo.
• Compatible indeterminado: el sistema tiene infinitas soluciones, lo que significa que los puntos fijos forman una recta completa.

En resumen, una transformación afín puede tener uno, ninguno o infinitos puntos fijos, pero nunca exactamente dos. Si aparecen al menos dos puntos fijos, estos definen una línea continua de puntos que permanecen invariantes bajo la transformación.

Propiedades adicionales

Las transformaciones afines presentan varias propiedades interesantes:

• Conservación de los paralelogramos
  Dado que mantienen el paralelismo, cualquier paralelogramo se transforma en otro paralelogramo, que puede estar desplazado, rotado, escalado o deformado, pero cuyos lados opuestos siguen siendo paralelos.
• Incidencia de las rectas
  Si dos rectas se cruzan en un punto $ P $, sus imágenes también se cruzarán en el punto $ P' $, imagen de $ P $.
• Secciones cónicas
  Una transformación afín conserva el tipo de una sección cónica: una elipse se transforma en otra elipse, una parábola en otra parábola y una hipérbola en otra hipérbola. En particular, una circunferencia - caso especial de elipse - suele transformarse en una elipse.
• Isometrías y semejanzas como subconjuntos
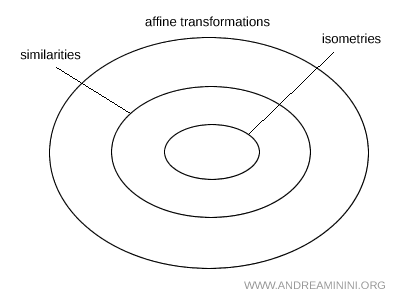
  Las isometrías y las semejanzas son casos particulares de transformaciones afines. El conjunto de todas las transformaciones afines incluye al de las semejanzas, y dentro de este se encuentran las isometrías.
  
• Las dilataciones como transformaciones afines
  Una dilatación es, en esencia, un tipo particular de transformación afín en el que los factores de escala \( h \) y \( k \) son ambos diferentes de cero, es decir, \( h \ne 0 \) y \( k \ne 0 \). Esta condición garantiza que la transformación mantenga su estructura geométrica y resulte plenamente invertible. $$ \begin{cases} x' = h x + p \\[4pt] y' = k y + q \end{cases} $$ En esta formulación, los coeficientes \( h \) y \( k \) indican en qué medida la figura original se estira o se comprime a lo largo de cada eje. El valor de \( h \) determina la deformación en la dirección del eje \( x \), mientras que \( k \) describe el mismo efecto sobre el eje \( y \). Gracias a estos parámetros, la dilatación puede representarse como una transformación que modifica la escala de la figura de manera diferenciada en cada dirección.

  Observación. Dado que los dos factores de escala son no nulos, el determinante de la matriz lineal asociada también es distinto de cero. Esto confirma que la aplicación es una transformación afín válida y reversible: $$ \begin{vmatrix} h & 0 \\ 0 & k \end{vmatrix} = hk \ne 0 $$

• Transformaciones afines isométricas: condiciones de isometría
  Una transformación afín es isométrica cuando se verifican las siguientes condiciones: $$ \begin{cases} a^2 + a'^2 = 1 \\ b^2 + b'^2 = 1 \\ ab + a'b' = 0 \end{cases} $$
• Transformaciones afines y semejanza: condiciones de semejanza
  Una transformación afín se convierte en una transformación de semejanza únicamente cuando se verifican las condiciones siguientes: $$ a^2 + a'^2 = b^2 + b'^2 $$ $$ ab + a'b' = 0 $$ Bajo estas condiciones, la razón de semejanza queda determinada por $$ k = \sqrt{a^2 + a'^2} = \sqrt{b^2 + b'^2} $$

Y así sucesivamente.