Punto fijo en geometría

Se llama punto fijo (o punto invariante) de una transformación geométrica a aquel que permanece en la misma posición después de aplicar dicha transformación.

Dicho de otro modo, si un punto conserva exactamente las mismas coordenadas antes y después de la transformación, se considera un punto fijo de esa transformación.

Formalmente, dada una función \( T: \mathbb{R}^2 \to \mathbb{R}^2 \), un punto \( P \) es un punto fijo si se cumple que \( T(P) = P \); es decir, el punto se transforma en sí mismo.

Por ejemplo, en una rotación en el plano, el centro \( P \) de rotación es un punto fijo, ya que permanece inmóvil.

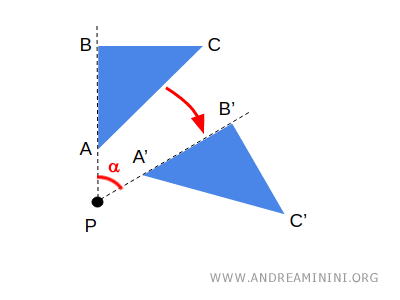
Una transformación puede tener varios puntos fijos.

Por ejemplo, en una simetría axial respecto a una recta \( r \), todos los puntos que pertenecen al eje de simetría \( r \) permanecen sin desplazamiento.

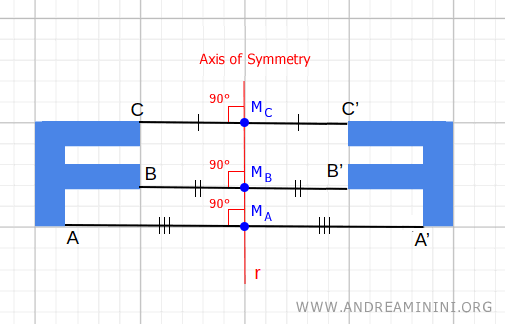
En determinados casos, todos los puntos de una figura pueden ser fijos.

Por ejemplo, una rotación completa de 360° alrededor de un punto central \( P \) deja cada punto exactamente en su lugar original.

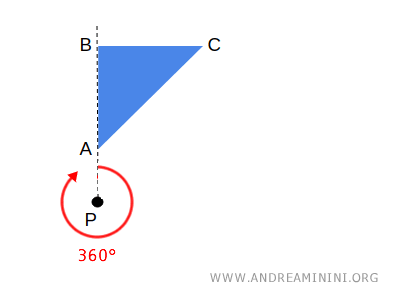
En este caso, todos los puntos son fijos, y se dice que la figura es puntualmente invariante bajo la transformación.

Cuando todos los puntos de una figura permanecen fijos, la transformación geométrica se denomina identidad.

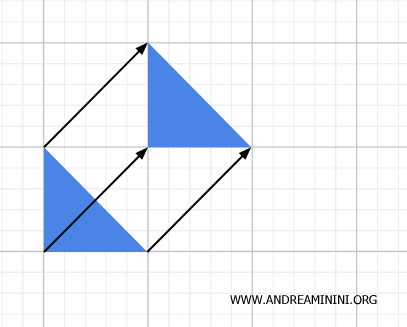
Nota: Puede ocurrir que ciertos puntos se transformen en otros puntos de la misma figura. En ese caso, no se consideran puntos fijos. Por ejemplo, tomemos la recta \( y = x \) y la transformación geométrica $$ T: \begin{cases} x' = x + 1 \\ y' = y + 1 \end{cases} $$ En este caso, cada punto de la figura transformada corresponde a otro punto de la recta original, aunque ninguno permanezca en su posición inicial.

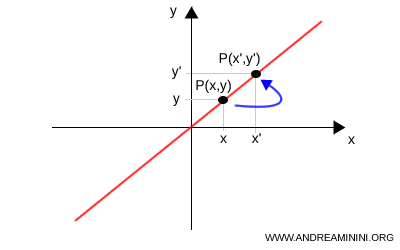
Conviene señalar que, en este ejemplo, la figura es una figura invariante bajo una isometría: la distancia entre cualquier par de puntos no se altera. Sin embargo, a pesar de esta invariancia, los puntos individuales no son fijos bajo la transformación.

En cambio, existen transformaciones que no tienen ningún punto fijo.

Por ejemplo, en una traslación, ningún punto permanece en su sitio, a menos que se trate de una traslación nula (sin desplazamiento).

Estos son solo algunos ejemplos de puntos fijos en el contexto de las transformaciones geométricas.

Nota: El concepto de punto fijo se extiende de forma natural del plano al espacio tridimensional. Un punto se considera fijo si sus coordenadas no varían después de la transformación. La única diferencia es que, en lugar de dos coordenadas \((x, y)\), el punto se describe mediante tres: \((x, y, z)\).

Y así sucesivamente.