Figura invariante

Se dice que una figura es invariante cuando permanece sin cambios tras ser sometida a una transformación.

En otras palabras, una figura es invariante si su imagen transformada coincide exactamente con la figura original.

Esto ocurre cuando una transformación geométrica no modifica la figura en modo alguno.

De manera más general, una figura se considera invariante bajo una transformación geométrica cuando ciertas propiedades - como distancias, ángulos o alineaciones - se conservan tras la aplicación de dicha transformación.

Este concepto es especialmente relevante en el estudio de simetrías, transformaciones geométricas y operaciones algebraicas. Desempeña un papel clave en el análisis de las isometrías y las transformaciones conformes.

Ejemplos

A continuación, algunos ejemplos ilustrativos del concepto:

• Una traslación nula genera una figura invariante, ya que cada punto se transforma en sí mismo. En este caso, el vector de traslación es el vector nulo. $$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$
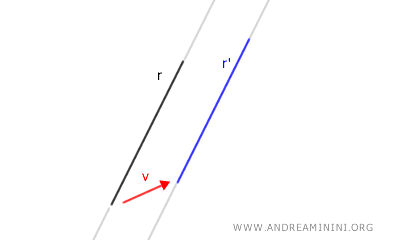
• Cuando se traslada una recta, el resultado es otra recta paralela, es decir, perteneciente a la misma familia. Por tanto, toda recta paralela puede considerarse invariante respecto a la original.
  
• Una rotación de 360° aplicada a una figura plana produce una figura invariante, ya que tras completar la vuelta, la figura permanece indistinguible del original.

En álgebra, un elemento se considera "invariante" respecto a una operación cuando, al aplicarle dicha operación junto con el elemento neutro, su valor no cambia. Por ejemplo, sumar un número cualquiera con cero (elemento neutro de la suma) no altera su valor: $$ x + 0 = x $$ Multiplicar cualquier número real por uno (elemento neutro de la multiplicación) también lo deja inalterado: $$ x \cdot 1 = x $$ En contextos más abstractos, como la teoría de grupos o la aritmética modular, el concepto de invarianza sigue siendo fundamental, aunque su tratamiento resulte más complejo.

Y así sucesivamente.

Diferencia entre invariancia puntual y global

En geometría, una figura se dice invariante respecto a una transformación cuando, al aplicarla, coincide exactamente con su imagen. Esta propiedad de invariancia puede manifestarse de dos maneras diferentes:

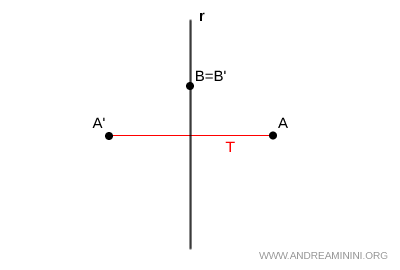
• Figura invariante puntual
  Una figura es invariante puntual cuando cada uno de sus puntos permanece fijo tras la transformación; es decir, todos conservan exactamente las mismas coordenadas.

  Ejemplo. En una simetría axial, todos los puntos situados sobre el eje de simetría (r) permanecen sin cambio. Así, el punto B se transforma en B', que ocupa la misma posición. Lo mismo ocurre con cualquier otro punto del eje. Por ello, el eje de simetría (r) es una figura invariante puntual.
  

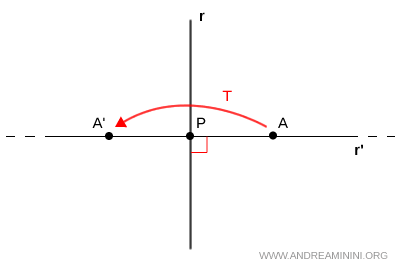
• Figura invariante global
  Una figura es invariante global cuando, tras la transformación, la figura completa coincide con su imagen, aunque sus puntos individuales se desplacen a posiciones distintas.

  Ejemplo. En una simetría axial, una recta (r') perpendicular al eje de simetría (r) se transforma en sí misma: los puntos cambian de lugar, pero la recta como objeto permanece inalterada. Por ejemplo, el punto A se convierte en A', que tiene coordenadas distintas pero sigue perteneciendo a la misma recta (r'). De este modo, la recta perpendicular (r') al eje es una figura invariante global.