Invariantes en las transformaciones geométricas
Los invariantes de una transformación geométrica son aquellas propiedades que permanecen inalteradas cuando una figura se somete a dicha transformación.
Los invariantes concretos dependen del tipo de transformación que se aplique.
Cada tipo de transformación geométrica posee su propio conjunto de invariantes característicos.
¿Por qué son importantes? Identificar los invariantes es fundamental para comprender las propiedades de las figuras geométricas y cómo se comportan al ser transformadas.
Un ejemplo práctico
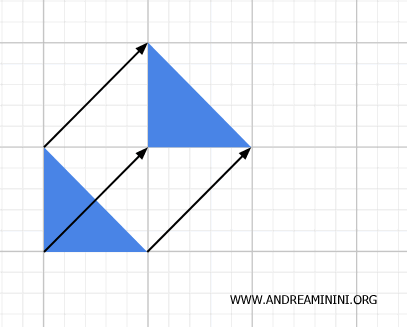
En una traslación, todos los puntos de una figura se desplazan en la misma dirección y a igual distancia.
Como consecuencia, se conservan las distancias entre puntos, así como la forma, el tamaño y la orientación de la figura.
Ejemplo 2
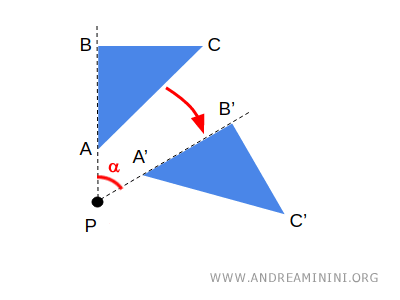
En una rotación, una figura gira alrededor de un punto fijo, P.
En este caso, los invariantes son el punto fijo, las distancias entre puntos, y la forma y el tamaño de la figura.
Ejemplo 3
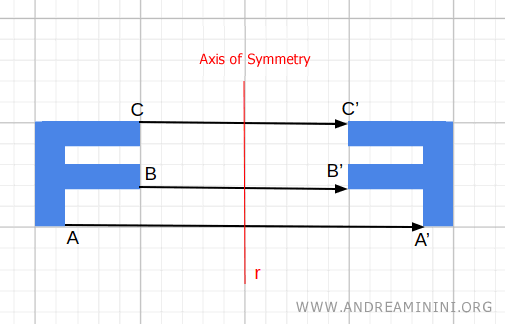
En una simetría axial, la figura se refleja respecto de una recta denominada eje de simetría.
Los invariantes en una reflexión son las distancias entre los puntos, la forma y el tamaño de la figura.
Nota: En general, una isometría (como la traslación, la rotación o la reflexión) es una transformación geométrica que preserva las distancias entre todos los pares de puntos. Por eso también se las conoce como "movimientos rígidos". Las propiedades invariantes de cualquier isometría son la distancia, la forma y el tamaño.
Ejemplo 4
En una homotecia (o dilatación), una figura se escala con respecto a un punto fijo llamado centro de homotecia.
En este caso, los invariantes son la razón entre las distancias respecto del centro de homotecia y la forma de la figura, aunque no su tamaño absoluto.
Nota: La homotecia no es una isometría. A diferencia de las isometrías, la homotecia modifica las distancias absolutas entre los puntos, y por tanto el tamaño de la figura, aunque mantiene sus proporciones y su forma.
Y así sucesivamente.