Traslación

La traslación es una transformación geométrica (isometría) que desplaza todos los puntos de una figura a la misma distancia y en la misma dirección, a lo largo de una línea determinada.

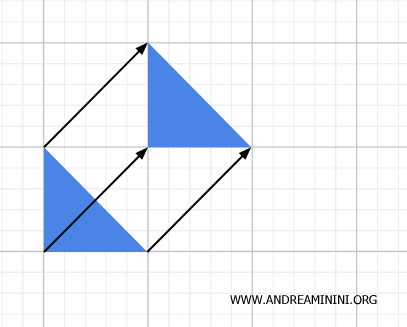
Este desplazamiento se representa mediante vectores llamados "vectores de traslación". La longitud o módulo de estos vectores indica la distancia recorrida durante el movimiento.

La dirección del vector marca el rumbo del desplazamiento, mientras que la punta de la flecha señala su sentido.

Dirección y sentido no son lo mismo. La dirección se refiere a la línea sobre la que ocurre el movimiento (por ejemplo, horizontal, vertical, diagonal, etc.), mientras que el sentido indica hacia qué lado se desplaza a lo largo de esa línea. Por ejemplo, un objeto que se mueve horizontalmente puede hacerlo hacia la derecha o hacia la izquierda. La dirección es horizontal, y el sentido nos dice si se dirige a un lado o al otro.

En geometría, una traslación en el plano se representa mediante un par ordenado (x;y):

• El primer valor, "x", indica el desplazamiento horizontal. Por convención, un valor positivo implica un movimiento hacia la derecha, y uno negativo hacia la izquierda.
• El segundo valor, "y", corresponde al desplazamiento vertical. Un valor positivo implica un movimiento hacia arriba, y uno negativo hacia abajo.

Es decir, ambos valores expresan cómo se mueve un punto a lo largo de los ejes horizontal (x) y vertical (y).

Los valores x e y son las componentes del desplazamiento.

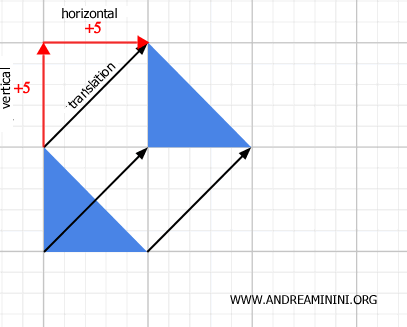
Cuando una figura geométrica se traslada, conserva su forma y tamaño originales, es decir, sigue siendo congruente con la figura inicial.

Después de la traslación, la distancia entre cualquier par de puntos de la figura permanece inalterada.

Por tanto, la traslación es un caso particular de isometría.

Nota. Una traslación también puede entenderse como una transformación geométrica que asocia a cada punto \( P \) del plano otro punto \( P' \), de manera que el vector \( \vec{PP'} \) coincida con un vector de traslación fijo \( \vec{v} \); es decir, \( \vec{PP'} = \vec{v} \).

Ecuaciones de la traslación

Las ecuaciones que describen una traslación se expresan en función de las componentes x e y del desplazamiento.

$$ \begin{cases} x' = x_0 + x \\ \\ y' = y_0 + y \end{cases} $$

Aquí, x' e y' son las nuevas coordenadas, mientras que x e y representan el desplazamiento respecto de las coordenadas originales x₀ e y₀.

Ejemplo

El rectángulo ABCD tiene sus vértices en las coordenadas A(1;1), B(2;1), C(1;3) y D(2;3) en el plano.

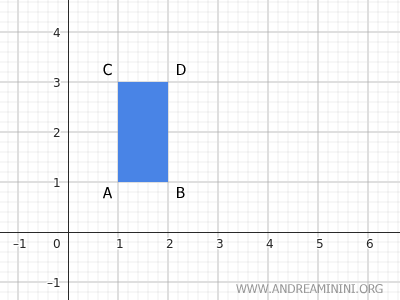
Consideremos ahora una traslación (3;1), que desplaza la figura 3 unidades hacia la derecha (x = 3) y 1 unidad hacia arriba (y = 1).

Aplicamos el desplazamiento horizontal de +3 a la coordenada x de cada punto:

$$ \begin{cases} A'(1+3;1) \\ B'(2+3;3) \\ C'(1+3;3) \\ D'(2+3;3) \end{cases} $$

$$ \begin{cases} A'(4;1) \\ B'(5;2) \\ C'(4;1) \\ D(5;2) \end{cases} $$

De este modo, toda la figura se desplaza hacia la derecha.

Las flechas rojas representan los vectores de desplazamiento correspondientes a la componente horizontal (x).

Todos los puntos de la figura se trasladan exactamente la misma distancia en la misma dirección. En este caso, 3 unidades hacia la derecha.

¿Qué es un vector? Un vector es una magnitud definida por su módulo (longitud), dirección y sentido. El origen del vector indica el punto de partida, y la punta de la flecha señala el punto de llegada.

Por ejemplo, un vector que va del punto A al punto A' se denomina "vector aplicado en A". En una traslación, el mismo vector se aplica a todos los puntos de la figura geométrica.

Luego aplicamos la traslación vertical de +1, desplazando los puntos A', B', C' y D' hacia arriba.

$$ \begin{cases} A'(4;1+1) \\ B'(5;2+1) \\ C'(4;1+1) \\ D(5;2+1) \end{cases} $$

$$ \begin{cases} A'(4;2) \\ B'(5;3) \\ C'(4;2) \\ D(5;3) \end{cases} $$

Estas son las coordenadas finales de la figura tras la traslación.

Es decir, hemos sumado algebraicamente las componentes (x;y) del vector v(3;1) a las coordenadas (x;y) de cada punto de la figura.

Traslación de una función

Trasladar una función \( y = f(x) \) consiste en desplazar cada punto de su gráfica mediante un vector \( \vec{v} = (a, b) \), sin alterar la forma de la curva. La función resultante queda expresada como: $$ y' = f(x' - a) + b $$

Partiendo de una función original \( y = f(x) \), aplicar una traslación significa modificar las coordenadas de todos sus puntos según el vector \( \vec{v} = (a, b) \): $$ \begin{cases} x' = x + a \\ y' = y + b \end{cases} $$

Para expresar la función trasladada en función de las nuevas coordenadas, reescribimos las variables originales de la siguiente manera:

$$ \begin{cases} x = x' - a \\ y = y' - b \end{cases} $$

Al sustituir estas expresiones en la ecuación original \( y = f(x) \), se obtiene:

$$ y' - b = f(x' - a) $$

$$ y' = f(x' - a) + b $$

Esta es la forma general de una función traslada.

La gráfica de la función se desplaza \( a \) unidades en sentido horizontal (a lo largo del eje x) y \( b \) unidades en sentido vertical (a lo largo del eje y).

Casos particulares

Existen dos casos destacables en los que la traslación se produce a lo largo de un único eje:

• Traslación vertical (eje y)
  Si se toma \( a = 0 \), el desplazamiento ocurre únicamente en dirección vertical: $$ y' = f(x) + b $$
• Traslación horizontal (eje x)
  Si se fija \( b = 0 \), el desplazamiento es exclusivamente horizontal: $$ y' = f(x - a) $$

Ejemplo

Consideremos la siguiente función cuadrática:

$$ y = 3x^2 $$

Queremos trasladarla mediante el vector \( \vec{v} = (4, 5) \), es decir, 4 unidades hacia la derecha y 5 unidades hacia arriba.

Al aplicar la fórmula general de la traslación, obtenemos:

$$ y = 3(x - 4)^2 + 5 $$

Esta nueva ecuación representa la misma parábola, ahora ubicada en una posición diferente dentro del plano cartesiano.

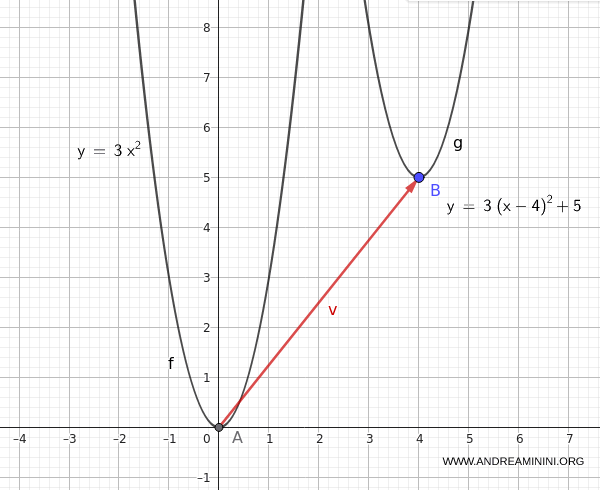
Nota. Este tipo de transformación es especialmente útil para estudiar cómo varía la posición de una gráfica sin que se vea afectada su forma. En otras palabras, la “identidad” de la función permanece intacta: solo cambia su ubicación en el plano.

La traslación como isometría

La traslación es una isometría porque mantiene inalterada la distancia entre puntos tras la transformación.

Demostración

Para demostrar que una traslación es una isometría, consideremos dos puntos cualesquiera A y B de una figura.

Aplicamos el mismo vector de traslación $ \vec{v} $ a ambos puntos, obteniendo las nuevas posiciones A' y B'.

En toda isometría, las distancias entre los puntos permanecen constantes.

Por tanto, debemos demostrar que la distancia entre A' y B' es igual a la distancia entre A y B.

Los segmentos AA' y BB' son congruentes y paralelos, ya que se ha aplicado el mismo vector a ambos puntos.

 

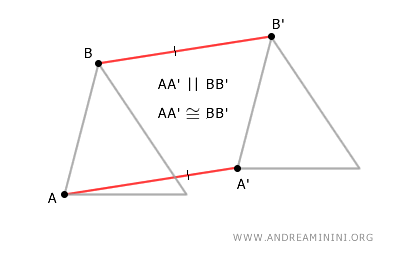
Si conectamos todos los puntos, obtenemos el cuadrilátero AA'B'B, que forma un paralelogramo.

En un paralelogramo, los lados opuestos son congruentes y paralelos entre sí.

Por tanto, los segmentos AB y A'B' también son congruentes, es decir, tienen la misma longitud:

$$ \overline{AB} \cong \overline{A' B'} $$

Esto demuestra que la distancia entre los puntos A y B no cambia tras la traslación.

En consecuencia, la traslación es una isometría.

Traslación en el espacio tridimensional

Una traslación en el espacio es una transformación geométrica que desplaza cada punto de un sólido mediante un vector \(\vec{v}\), manteniendo constantes las distancias y los ángulos.

Si un punto \( P(x, y, z) \) se traslada mediante el vector \( \vec{v} = (a, b, c) \), sus nuevas coordenadas serán:

\[ P'(x', y', z') = (x + a, y + b, z + c). \]

Esto demuestra que la traslación en el espacio tridimensional consiste simplemente en sumar el vector de desplazamiento a cada coordenada.

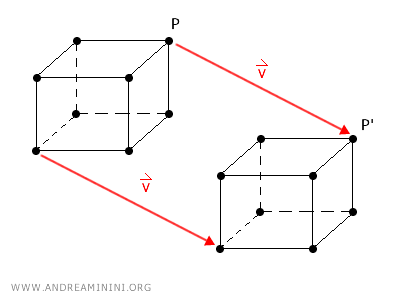
En tres dimensiones, la traslación sigue las mismas reglas que en el plano, con la diferencia de que se aplica también sobre el eje z.

Propiedades fundamentales de la traslación en el espacio

La traslación conserva todas las propiedades geométricas del sólido, por lo que la figura trasladada es perfectamente congruente con la original.

En concreto, preserva la longitud de los segmentos, las medidas angulares, el paralelismo y la colinealidad de los puntos.

Por eso, la traslación espacial también se clasifica como una isometría, ya que mantiene constantes las distancias.

Además, es una transformación afín, porque conserva el paralelismo, la alineación de puntos y las relaciones proporcionales entre segmentos alineados.

Notas

A continuación, se presentan algunas observaciones adicionales sobre la traslación:

• La composición de varias traslaciones también es una traslación
  La aplicación sucesiva de dos o más traslaciones equivale a una sola traslación, cuyo vector es la suma vectorial de los vectores iniciales. Es decir, trasladar una figura varias veces seguidas equivale a aplicar una única traslación con el vector resultante.
  

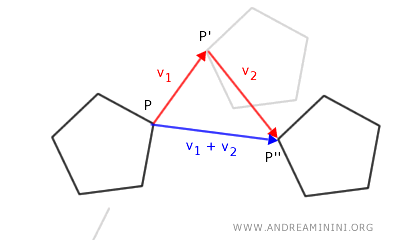
  En geometría analítica, la composición de dos traslaciones definidas por los vectores \( \vec{v}_1 \) y \( \vec{v}_2 \) da lugar a otra traslación, cuyo vector es \( \vec{v}_1 + \vec{v}_2 \).

• Propiedad conmutativa
  La composición de dos traslaciones cuyos vectores son \( \vec{v}_1 \) y \( \vec{v}_2 \) es conmutativa, es decir, \( \vec{v}_1 \circ \vec{v}_2 = \vec{v}_2 \circ \vec{v}_1 \).
• La traslación de una recta da como resultado una recta paralela o coincidente
  Si el vector de traslación tiene la misma dirección que la recta, el resultado es una recta coincidente, independientemente del sentido.
  
  Si la dirección del vector es distinta, se obtiene una recta paralela.
  
• Una traslación nula equivale a la transformación identidad
  Se considera nula una traslación cuyo vector es el vector nulo, es decir, un vector de módulo cero y sin dirección ni sentido definidos.$$ \vec{v} =  \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ Al sumar el vector nulo a cualquier punto, sus coordenadas permanecen inalteradas. $$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ Por tanto, una traslación nula deja la figura exactamente igual, lo que equivale a una transformación identidad.

  ¿Qué es una figura invariante? Una figura se dice invariante si, tras una transformación, su imagen coincide exactamente con la figura original. Por ejemplo, una traslación nula genera una figura invariante.

• Traslaciones horizontales y verticales
  Las traslaciones horizontales y verticales constituyen casos particulares de traslaciones lineales. Cuando el vector de traslación es \( \vec{v}(a, 0) \), todos los puntos del plano se desplazan horizontalmente; si el vector es \( \vec{v}(0, b) \), el desplazamiento es vertical.
• Puntos fijos
  Toda traslación distinta de la identidad carece de puntos fijos.

  Nota. Una traslación equivale a la transformación identidad únicamente cuando ambos componentes del vector de traslación son cero: \( \vec{v}(0, 0) \). Si al menos uno de los componentes de \( \vec{v}(a, b) \) es distinto de cero, entonces cada punto del plano se desplaza según la regla: $$ \begin{cases} x' = x + a \\ \\ y' = y + b \end{cases} $$ Por lo tanto, ningún punto permanece invariante bajo esta transformación.

• Las rectas paralelas al vector de traslación permanecen invariantes como conjunto
  Bajo una traslación, toda recta paralela al vector de traslación se transforma en sí misma: la isometría conserva la recta en su totalidad, aunque cada uno de sus puntos se desplace.
  

Y así sucesivamente.