Composición de transformaciones geométricas
Componer transformaciones geométricas consiste en aplicar dos o más transformaciones de manera sucesiva sobre un mismo objeto. $$ s \circ t $$
Se lee como "s compuesta con t", donde t es la primera transformación que se aplica, seguida de s. Por lo tanto, la composición se interpreta de derecha a izquierda.
Un ejemplo práctico
Tomemos como punto de partida una figura geométrica inicial.
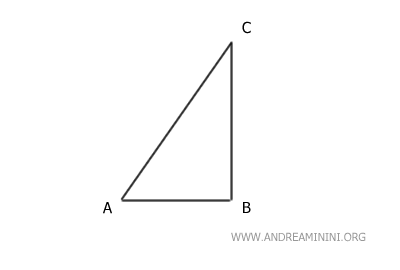
Primero aplicamos una rotación de 90° en torno al punto A, que actúa como centro de rotación.
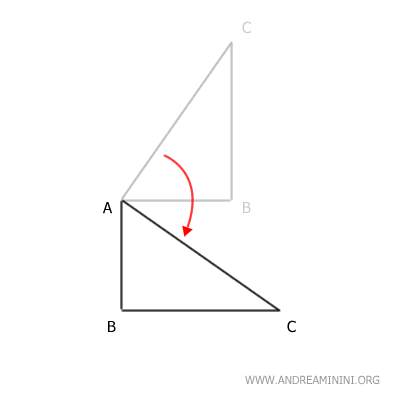
Después, aplicamos una segunda transformación al resultado. Por ejemplo, una traslación a lo largo del segmento AB.
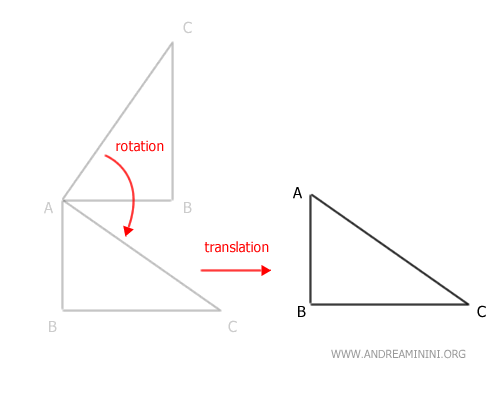
El resultado final es la figura obtenida mediante la composición de estas dos transformaciones geométricas.
Nota: Una transformación geométrica modifica una figura siguiendo ciertas reglas, sin alterar propiedades fundamentales como distancias, ángulos o paralelismos. Entre las transformaciones más comunes se encuentran las traslaciones, rotaciones, simetrías y homotecias.
Es importante tener en cuenta que la composición de transformaciones geométricas no es conmutativa.
Esto significa que el orden en que se aplican las transformaciones influye directamente en el resultado final.
Composición de transformaciones en el espacio
Las transformaciones geométricas también pueden componerse cuando se aplican a cuerpos tridimensionales.
Si aplico una transformación a una figura sólida, obtengo una nueva figura transformada. Al aplicar otra transformación sobre esta nueva figura, obtengo una transformación compuesta que lleva directamente de la figura original a la final.
Ejemplo
Consideremos un sólido en el espacio, \( \mathcal{F} \), como una pirámide de base cuadrada. Primero aplicamos una traslación, a la que llamaremos transformación \( t_1 \), obteniendo así un nuevo sólido, \( \mathcal{F}_1 \).
Luego realizamos una simetría respecto de un plano, que será la segunda transformación, \( t_2 \), generando otro sólido transformado, \( \mathcal{F}_2 \).
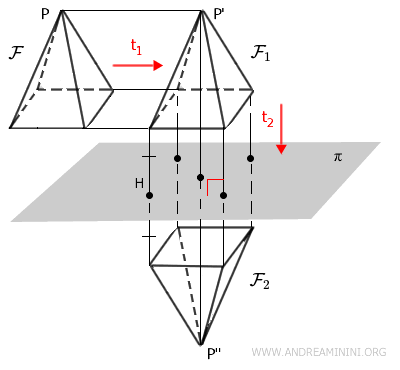
Esta secuencia de pasos representa una transformación compuesta, \( t_2 \circ t_1 \), donde primero se aplica \( t_1 \) y luego \( t_2 \).
En lugar de efectuar ambas transformaciones por separado, es posible aplicar directamente la composición \( t_2 \circ t_1 \) a la figura original \( \mathcal{F} \), obteniendo directamente el sólido transformado \( \mathcal{F}_2 \).
Nota: En el espacio tridimensional, el orden de las transformaciones es crucial, ya que en general la composición no es conmutativa. Es decir, cambiar el orden de aplicación puede dar lugar a resultados completamente diferentes.
Composición en geometría analítica
Dadas dos transformaciones $t_1$ y $t_2$, la composición $t_2 \circ t_1$ se define como: $$(t_2 \circ t_1)(P) = t_2(t_1(P))$$ donde $P$ es un punto cualquiera del plano.
En otras palabras, primero se aplica la transformación $t_1$ al punto $P$, obteniendo $P_1 = t_1(P)$. Luego se aplica $t_2$ sobre $P_1$, obteniendo finalmente $P_2 = t_2(P_1)$.
Así, si $t_1: (x, y) \mapsto (x', y')$ y $t_2: (x', y') \mapsto (x'', y'')$, la composición $t_2 \circ t_1$ puede escribirse como:
$$ t_2 \circ t_1 : (x, y) \mapsto (x'', y'') = t_2(t_1(x, y)) $$
Como ya se mencionó, la composición no es conmutativa, por lo que el orden de aplicación de las transformaciones es fundamental:
$$ t_2 \circ t_1 \ne t_1 \circ t_2 $$
Sin embargo, se cumple la propiedad asociativa:
$$ t_1 \circ ( t_2 \circ t_3 ) = ( t_1 \circ t_2 ) \circ t_3 $$
Esto significa que el modo en que agrupamos las transformaciones no afecta al resultado final.
Ya sea que primero compongamos $t_2$ con $t_3$ y luego apliquemos $t_1$, o que primero compongamos $t_1$ con $t_2$ y luego apliquemos el resultado a $t_3$, la transformación global será la misma.
Nota: Si componemos una transformación $t_1$ con su inversa $t_1^{-1}$, obtenemos la transformación identidad, que deja todos los puntos invariantes: $$ t_1 \circ t_1^{-1} = t_1^{-1} \circ t_1 = i $$ En este caso particular, la composición sí es conmutativa.
Ejemplo
Veamos las siguientes dos transformaciones en el plano cartesiano:
La transformación $t_1$ refleja un punto respecto al eje $x$:
$$ t_1: \begin{cases} x' = x \\ y' = -y \end{cases} $$
La transformación $t_2$ traslada un punto 2 unidades a la derecha y 3 unidades hacia arriba:
$$ t_2: \begin{cases} x'' = x' + 2 \\ y'' = y' + 3 \end{cases} $$
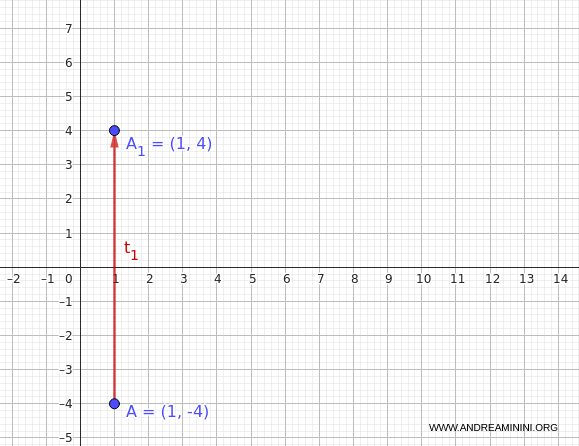
Tomamos como punto de partida $A(1, -4)$.
Calculamos ahora la composición $t_2 \circ t_1$, es decir, aplicamos primero $t_1$ y luego $t_2$.
Aplicando $t_1$ a $A(1, -4)$ obtenemos:
$$ A_1 = t_1(1, -4) = (1, 4) $$
Ahora, al aplicar $t_2$ a $A_1(1, 4)$ se obtiene:
$$ A_2 = t_2(1, 4) = (1 + 2, 4 + 3) = (3, 7) $$
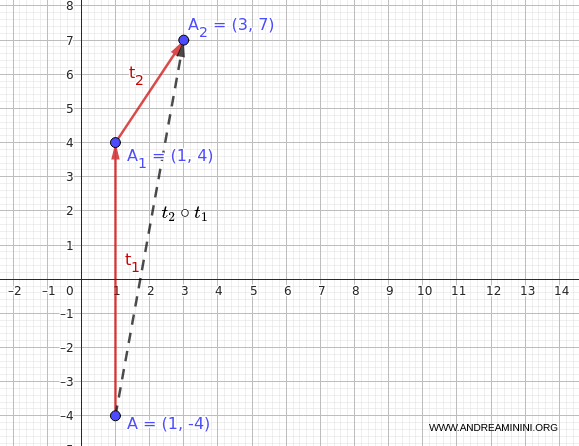
Por lo tanto, la composición $t_2 \circ t_1$ aplicada a $A$ da como resultado el punto $(3, 7)$:
$$ (t_2 \circ t_1)(A) = (3, 7) $$
Nota: Si combinamos ambas transformaciones en una sola operación, la composición resulta ser: $$ t_2 \circ t_1 : \begin{cases} x'' = x + 2 \\ y'' = -y + 3 \end{cases} $$
Ejemplo 2
Volvemos a considerar las mismas dos transformaciones y el punto inicial $A(1, -4)$:
$$ t_1: \begin{cases} x' = x \\ y' = -y \end{cases} $$
$$ t_2: \begin{cases} x'' = x' + 2 \\ y'' = y' + 3 \end{cases} $$
Esta vez, calculamos la composición en orden inverso:
$$t_1 \circ t_2$$
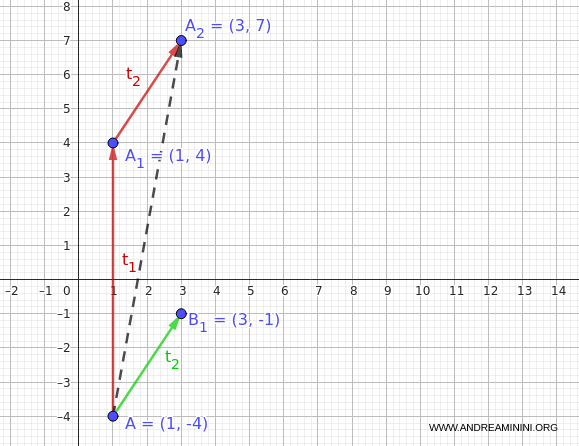
Es decir, primero aplicamos $t_2$ y luego $t_1$.
Aplicando $t_2$ a $A(1, -4)$ se obtiene:
$$ B_1 = t_2(1, -4) = (1 + 2, -4 + 3) = (3, -1) $$
Después, aplicamos $t_1$ a $B_1(3, -1)$ y obtenemos:
$$ B_2 = t_1(3, -1) = (3, 1) $$
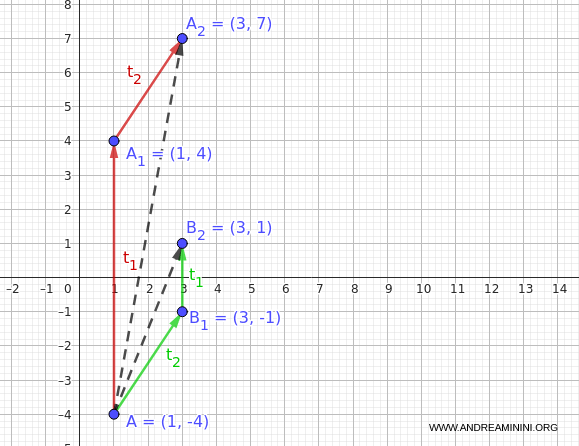
Por tanto, la composición $t_1 \circ t_2$ aplicada a $A$ da como resultado el punto $(3, 1)$:
$$ (t_1 \circ t_2)(A) = (3, 1) $$
Nota: Las dos composiciones (en rojo y verde) conducen a resultados distintos: $$(t_2 \circ t_1)(A) = (3, 7)$$ $$(t_1 \circ t_2)(A) = (3, 1)$$ Lo cual confirma que, en general, la composición no es conmutativa: $$ t_2 \circ t_1 \ne t_1 \circ t_2 $$
Ejemplo 3
Consideremos ahora la transformación $t_1$, que traslada un punto 4 unidades a la derecha y 2 unidades hacia abajo:
$$ t_1: \begin{cases} x' = x + 4 \\ y' = y - 2 \end{cases} $$
Su inversa $t_1^{-1}$ anula el efecto de la original:
$$ t_1^{-1}: \begin{cases} x'' = x' - 4 \\ y'' = y' + 2 \end{cases} $$
Componemos ahora ambas transformaciones:
$$t_1^{-1} \circ t_1$$
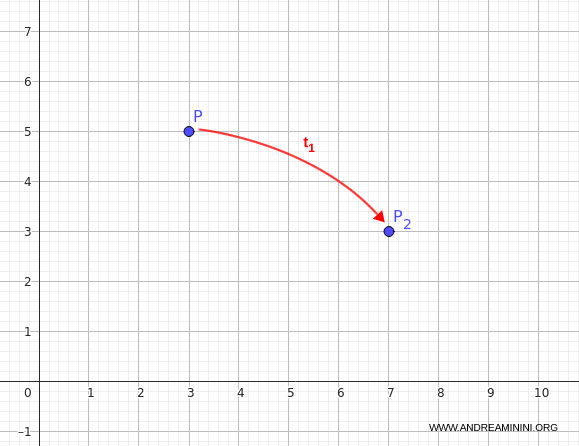
Tomamos un punto cualquiera, por ejemplo:
$$ P(3, 5) $$
Aplicamos $t_1$ sobre $P$:
$$ P_2 = t_1(3, 5) = (3 + 4, 5 - 2) = (7, 3) $$
Ahora aplicamos $t_1^{-1}$ a $P_2$:
$$ t_1^{-1}(7, 3) = (7 - 4, 3 + 2) = (3, 5) $$
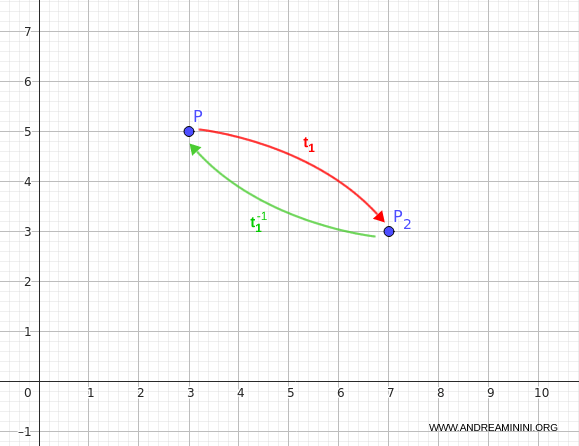
Por tanto, la composición nos devuelve exactamente al punto original:
$$ (t_1^{-1} \circ t_1)(3, 5) = (3, 5) $$
Esto confirma que componer una transformación con su inversa da como resultado la transformación identidad, que no modifica ningún punto del plano:
$$ t_1^{-1} \circ t_1 = \text{id} $$
Y así sucesivamente.