Transformaciones geométricas inversas

Una transformación geométrica inversa es aquella que revierte los efectos de una transformación geométrica previamente aplicada.

Dicho de otro modo, la transformación inversa devuelve una figura a su posición original cuando se aplica después de la transformación inicial.

Al igual que la transformación original, su inversa también se considera una transformación geométrica.

Nota: Desde el punto de vista matemático, si una transformación se representa mediante una matriz A, su inversa se denota por la matriz A^-1, de manera que al multiplicarlas se obtiene la matriz identidad: $$ A \cdot A^{-1} = I $$. Esto significa que aplicar A seguida de A^-1 no modifica el objeto, y este mismo principio se aplica en geometría.

Un ejemplo práctico

Partamos de una figura geométrica situada en el plano.

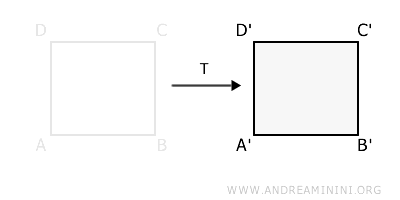
Aplicamos una traslación T que desplaza la figura 5 centímetros hacia la derecha.

Esta operación constituye una transformación geométrica.

La transformación inversa, T^-1, traslada la figura 5 centímetros hacia la izquierda.

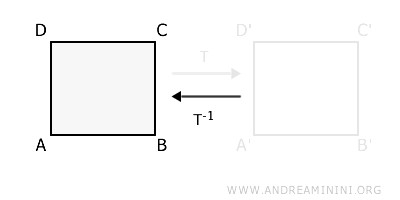
En definitiva, la transformación inversa deshace el efecto de la transformación inicial.

Al componer la transformación T con su inversa T^-1, se obtiene la transformación identidad I.

$$ T \circ T^{-1} = I $$

Ejemplo 2

Volvamos a utilizar la misma figura del ejemplo anterior.

Ahora aplicamos una rotación R de 45° en sentido horario, tomando como centro el punto A.

Al igual que la traslación, la rotación es una transformación geométrica.

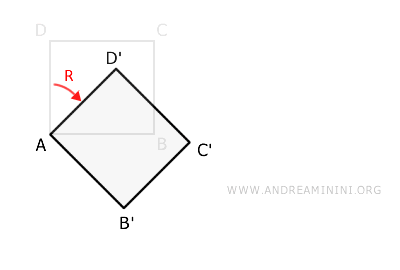
Su transformación inversa, R^-1, consiste en una rotación de 45° en sentido antihorario.

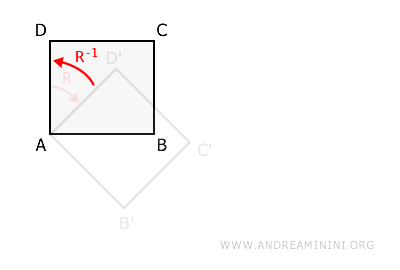
Una vez más, la transformación inversa anula el efecto de la transformación original.

La composición de R con su inversa R^-1 da lugar a la transformación identidad I.

$$ R \circ R^{-1} = I $$

Y así sucesivamente.