Transformaciones Geométricas
Una transformación geométrica es una correspondencia biunívoca que asigna a cada punto de un plano (o del espacio) un único punto en ese mismo plano (o espacio).
Existen distintos tipos de transformaciones geométricas, como las rotaciones, traslaciones, isometrías, entre otras.
De manera más formal, una transformación geométrica es toda función invertible T que asocia a cada punto P de un conjunto no vacío X un punto P′ perteneciente al conjunto Y.
$$ T: X \rightarrow Y $$
En este contexto, el conjunto Y representa la imagen T(X) del conjunto X bajo la acción de la transformación T.
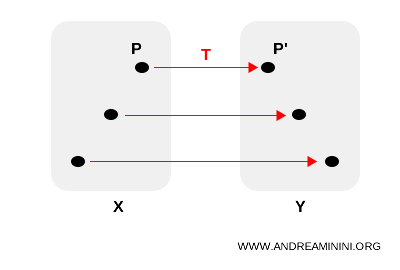
El punto P′ en Y se denomina imagen o transformado de P, mientras que P en X se conoce como preimagen o transformado inverso.
En términos simples, las transformaciones geométricas son operaciones matemáticas que modifican la posición o la forma de un objeto dentro de un espacio geométrico. Estas transformaciones pueden aplicarse a distintos elementos, como puntos, rectas, figuras planas o cuerpos sólidos.
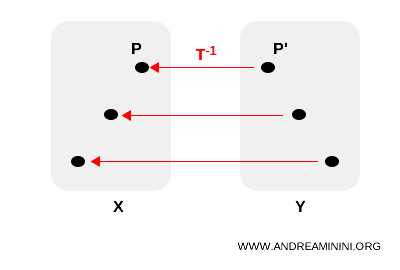
Como se trata de una correspondencia biunívoca, existe también una transformación inversa $ T^{-1}: Y \rightarrow X $, que permite recuperar el punto original del conjunto X a partir de su imagen en Y.
Las propiedades geométricas que se conservan tras aplicar una transformación reciben el nombre de invariantes.
Un Ejemplo
Consideremos una figura geométrica formada por los puntos A, B y C.
Si rotamos la figura un ángulo determinado α, se establece una correspondencia entre los puntos A y A', B y B', C y C'.
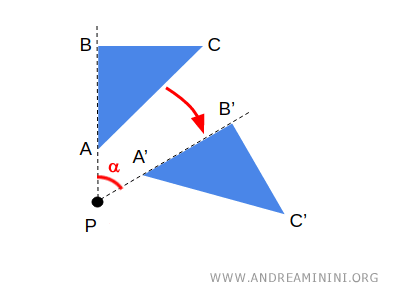
Los puntos A', B' y C', obtenidos tras la transformación, se denominan imágenes o puntos transformados de los puntos A, B y C, respectivamente.
Si interpretamos la rotación como una función biyectiva f, podemos expresarlo así:
$$ A' = f(A) $$
$$ B' = f(B) $$
$$ C' = f(C) $$
Esta notación se lee como "A' es igual a f de A", y lo mismo se aplica a los demás puntos.
Naturalmente, esta relación se extiende a todos los puntos y segmentos de la figura.
Por ejemplo, el segmento A'B' es la imagen del segmento AB.
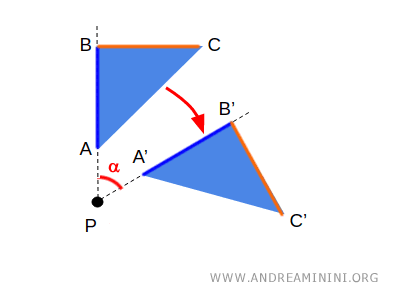
Este es un ejemplo concreto de transformación geométrica.
Nota. En este caso, el punto P coincide con su imagen. Es decir, su posición no varía tras la rotación. A este tipo de punto se lo denomina punto fijo.
Tipos de Transformaciones Geométricas
Existen diferentes tipos de transformaciones geométricas.
A continuación, se presentan las principales:
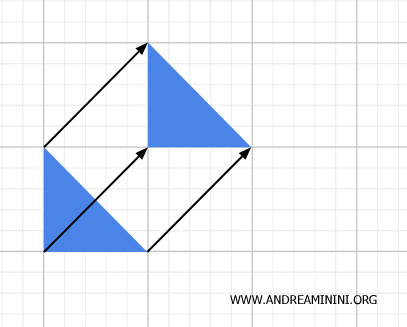
- Traslación
Consiste en desplazar todos los puntos de una figura una distancia constante en una dirección determinada. La figura trasladada conserva exactamente la forma y el tamaño de la original.
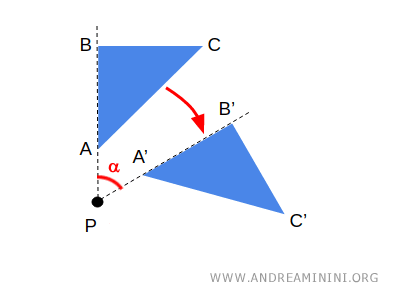
- Rotación
Es el movimiento circular de una figura alrededor de un punto fijo, llamado centro de rotación. La distancia de cada punto respecto al centro se mantiene constante.
- Reflexión (o Simetría Axial)
Es una transformación que invierte una figura respecto a una recta (eje de simetría), generando una imagen especular.
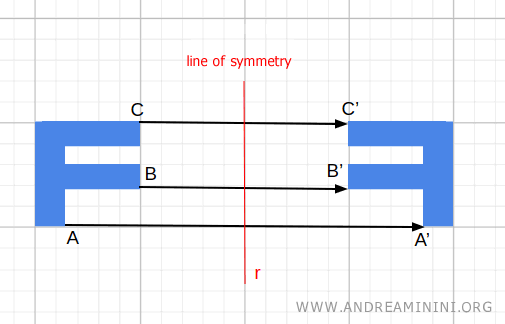
- Isometría
Las isometrías son transformaciones que conservan las distancias entre puntos y las dimensiones de los objetos. Entre ellas se encuentran la traslación, la rotación y la reflexión. - Homotecia (Dilatación o Escalado)
Se trata de una transformación que modifica el tamaño de una figura, conservando sus proporciones y su forma general. Esto se logra multiplicando por un factor constante las distancias de todos los puntos respecto a un punto fijo, llamado centro de dilatación.
Transformaciones Geométricas en Geometría Analítica
Una transformación geométrica puede representarse mediante un sistema de ecuaciones lineales que determina una única solución para cada par de coordenadas: $$ \begin{cases} x' = ax + by + c \\ y' = dx + ey + f \end{cases} $$ En este caso, $x$ e $y$ son las coordenadas originales, $x'$ e $y'$ son las coordenadas transformadas, y $a, b, c, d, e, f$ son los coeficientes de la transformación.
En términos simples, a cada punto $(x, y)$ le corresponde una única imagen $(x', y')$, y a cada $(x', y')$ le corresponde una única preimagen $(x, y)$.
Esta correspondencia biunívoca se cumple únicamente cuando el sistema tiene solución única, es decir, cuando el determinante es distinto de cero.
$$ \Delta = \begin{vmatrix} a & b \\ d & e \end{vmatrix} = ae - bd \neq 0 $$
¿Por qué el sistema debe ser lineal? Las transformaciones lineales garantizan continuidad (sin saltos ni rupturas) y biyección (cada punto se transforma de manera única y reversible). Un determinante distinto de cero asegura que la transformación sea invertible y esté bien definida en todo el plano o espacio.
Ejemplo
Consideremos el siguiente sistema:
$$ \begin{cases} x' = 2x - 3y + 5 \\ y' = x + 4y - 2 \end{cases} $$
Se trata de una transformación afín, ya que las expresiones lineales están acompañadas de términos constantes (5 y -2).
Podemos reescribirlo de forma equivalente:
$$ \begin{cases} 2x - 3y = x' - 5 \\ x + 4y = y' + 2 \end{cases} $$
La matriz de coeficientes es:
$$\begin{pmatrix} 2 & -3 \\ 1 & 4 \end{pmatrix}$$
Calculemos ahora el determinante para verificar si el sistema tiene solución única:
$$ \Delta = \begin{vmatrix} 2 & -3 \\ 1 & 4 \end{vmatrix} = 2 \cdot 4 - (-3) \cdot 1 = 8 + 3 = 11 \ne 0 $$
Como el determinante es distinto de cero, la transformación es invertible y biyectiva, lo que confirma que se trata de una transformación geométrica válida.
Esto significa que cada punto tiene una imagen y una preimagen bien definidas.
Ejemplo. Apliquemos la transformación al punto $A(1, 2)$: $$ \begin{cases} x' = 2 \cdot 1 - 3 \cdot 2 + 5 = 2 - 6 + 5 = 1 \\ y' = 1 + 4 \cdot 2 - 2 = 1 + 8 - 2 = 7 \end{cases} $$ Por lo tanto, $A(1, 2) \mapsto A'(1, 7)$ 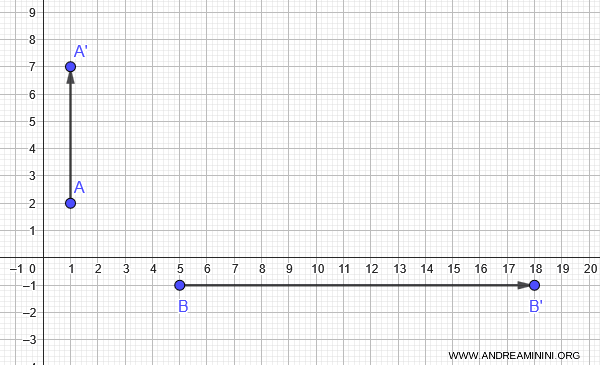
Ahora consideremos $B(5, -1)$: $$ \begin{cases} x' = 2 \cdot 5 - 3 \cdot (-1) + 5 = 10 + 3 + 5 = 18 \\ y' = 5 + 4 \cdot (-1) - 2 = 5 - 4 - 2 = -1 \end{cases} $$ Así que $B(5, -1) \mapsto B'(18, -1)$
Para determinar la transformación inversa, es decir, para hallar $x$ e $y$ a partir de $x'$ e $y'$, podemos aplicar la regla de Cramer o el método de la matriz inversa.
Reescribimos el sistema:
$$ \begin{cases} 2x - 3y = x' - 5 \\ x + 4y = y' + 2 \end{cases} $$
Utilizaremos la regla de Cramer, sabiendo que $ \Delta = 11 $.
Reemplazamos la primera columna por los términos independientes para obtener $ \Delta_x $:
$$ \Delta_x = \begin{vmatrix} x' - 5 & -3 \\ y' + 2 & 4 \end{vmatrix} $$
$$ \Delta_x = 4(x' - 5) + 3(y' + 2) = 4x' - 20 + 3y' + 6 = 4x' + 3y' - 14 $$
Por tanto: $$ x = \frac{ \Delta_x }{ \Delta } = \frac{4x' + 3y' - 14}{11} $$
Ahora calculamos $ \Delta_y $ reemplazando la segunda columna:
$$ \Delta_y = \begin{vmatrix} 2 & x' - 5 \\ 1 & y' + 2 \end{vmatrix} $$
$$ \Delta_y = 2(y' + 2) - (x' - 5) = 2y' + 4 - x' + 5 = -x' + 2y' + 9 $$
Entonces: $$ y = \frac{ \Delta_y }{ \Delta } = \frac{-x' + 2y' + 9}{11} $$
La transformación inversa queda así:
$$ \begin{cases} x = \dfrac{4x' + 3y' - 14}{11} \\ y = \dfrac{-x' + 2y' + 9}{11} \end{cases} $$
Esto demuestra que la transformación es reversible: la biyección está garantizada.
Desde el punto de vista geométrico, significa que a cada punto del plano le corresponde una única imagen, y a cada imagen una única preimagen.
Nota. También es posible deducir las ecuaciones inversas utilizando la matriz inversa de los coeficientes. Partimos nuevamente del sistema: $$ \begin{cases} 2x - 3y = x' - 5 \\ x + 4y = y' + 2 \end{cases} $$
Expresamos el sistema en forma matricial:
$$ A \cdot \vec{x} = \vec{b} $$
Donde $A = \begin{pmatrix} 2 & -3 \\ 1 & 4 \end{pmatrix}$ es la matriz de coeficientes, $\vec{x} = \begin{pmatrix} x \\ y \end{pmatrix}$ es el vector incógnita, y $\vec{b} = \begin{pmatrix} x' - 5 \\ y' + 2 \end{pmatrix}$ es el vector de términos independientes.
$$ \begin{pmatrix} 2 & -3 \\ 1 & 4 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x' - 5 \\ y' + 2 \end{pmatrix} $$
Despejamos $\vec{x}$ de la siguiente manera:
$$ \vec{x} = A^{-1} \cdot \vec{b} $$
La matriz inversa $A^{-1}$ se calcula así: $$ A^{-1} = \frac{1}{\det(A)} \begin{pmatrix} e & -b \\ -d & a \end{pmatrix} = \frac{1}{11} \begin{pmatrix} 4 & 3 \\ -1 & 2 \end{pmatrix} $$
Sustituyendo en la ecuación matricial: $$ \vec{x} = \frac{1}{11} \begin{pmatrix} 4 & 3 \\ -1 & 2 \end{pmatrix} \begin{pmatrix} x' - 5 \\ y' + 2 \end{pmatrix} $$
Calculamos cada componente:
$$ x = \frac{1}{11} \left[ 4(x' - 5) + 3(y' + 2) \right] = \frac{4x' + 3y' - 14}{11} $$
$$ y = \frac{1}{11} \left[ -1(x' - 5) + 2(y' + 2) \right] = \frac{-x' + 2y' + 9}{11} $$
Por tanto, la transformación inversa es: $$ \begin{cases} x = \dfrac{4x' + 3y' - 14}{11} \\ y = \dfrac{-x' + 2y' + 9}{11} \end{cases} $$
El resultado coincide con el obtenido por la regla de Cramer.
Cómo Aplicar una Transformación Geométrica a una Función
Cuando se trabaja con una función - por ejemplo, una parábola como \( y = x^2 \) - y se desea observar cómo se modifica tras una transformación geométrica, es necesario trasladar sus puntos siguiendo un procedimiento concreto.
- Calcula la inversa de la transformación \( t \), es decir, expresa \( x \) e \( y \) en función de las nuevas variables \( x' \) e \( y' \).
- Sustituye esas expresiones en la ecuación original.
- Reescribe la ecuación en función de las nuevas coordenadas \( x' \) e \( y' \).
Ejemplo
Partimos de la función:
$$ y = x^2 $$
Y aplicamos la transformación geométrica:
$$ t: \begin{cases} x' = x + 1 \\ y' = y - 2 \end{cases} $$
Primero obtenemos la transformación inversa, es decir, expresamos \( x \) e \( y \) en función de \( x' \) e \( y' \):
$$ \begin{cases} x' = x + 1 \Rightarrow x = x' - 1 \\ y' = y - 2 \Rightarrow y = y' + 2 \end{cases} $$
Así, la transformación inversa \( t^{-1} \) es:
$$ t^{-1} : \begin{cases} x = x' - 1 \\ y = y' + 2 \end{cases} $$
Sustituimos \( x = x' - 1 \) y \( y = y' + 2 \) en la ecuación original:
$$ y = x^2 $$
$$ y' + 2 = (x' - 1)^2 $$
$$ y' + 2 = x'^2 - 2x' + 1 $$
$$ y' = x'^2 - 2x' + 1 - 2 $$
$$ y' = x'^2 - 2x' - 1 $$
Por tanto, tras la transformación, la parábola \( y = x^2 \) se convierte en \( y' = x'^2 - 2x' - 1 \).
Esta transformación desplaza la gráfica una unidad hacia la derecha (porque \( x' = x + 1 \)) y dos unidades hacia abajo (ya que \( y' = y - 2 \)).
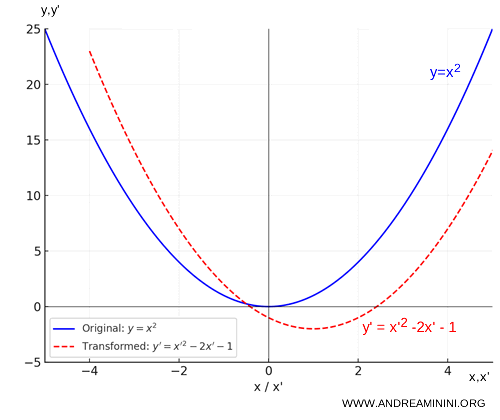
La parábola cambia de posición, pero su forma general permanece inalterada.
Observaciones
Algunas observaciones y apuntes complementarios:
- Las transformaciones geométricas pueden expresarse mediante ecuaciones, matrices o funciones. Por ejemplo, una traslación se representa sumando un vector constante a cada punto, mientras que una rotación puede expresarse mediante una matriz de rotación. Y así sucesivamente.
Y así sucesivamente.