Transformaciones proyectivas

Las transformaciones proyectivas son modificaciones topológicas que se generan al proyectar todos los puntos de una figura en el espacio desde un centro de proyección P.

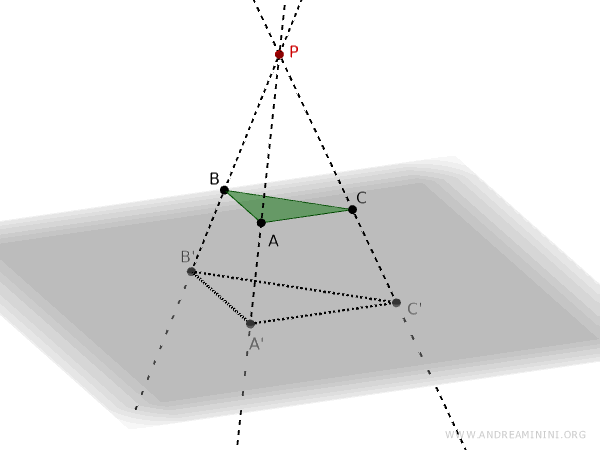
De forma más intuitiva, una transformación proyectiva puede imaginarse como la sombra que proyecta un objeto.

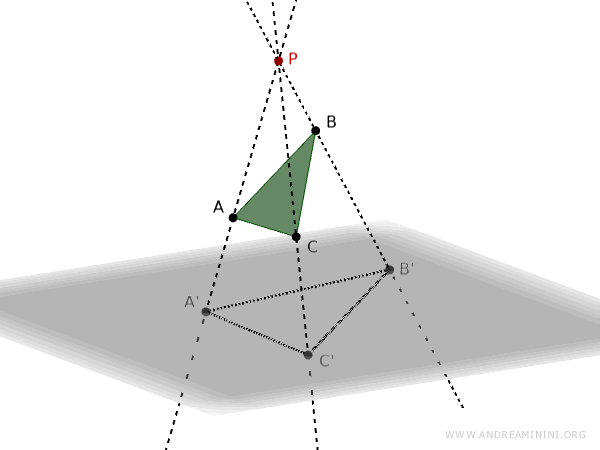
Tomemos como ejemplo un punto de proyección P, un triángulo ABC y un plano de proyección.

Se traza una recta que pasa por los puntos P y A, denominada rayo proyectante, y se determina el punto de intersección A' sobre el plano.

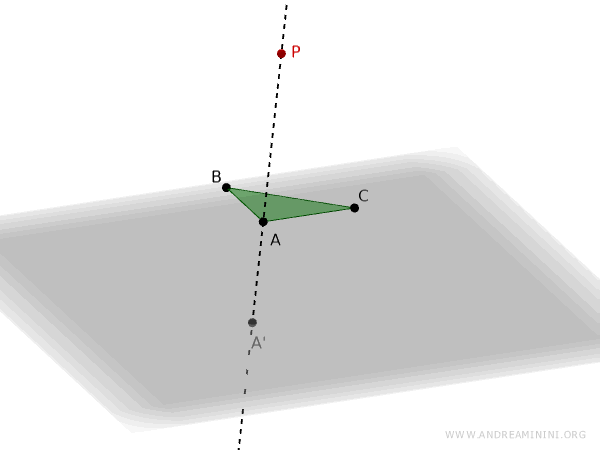
Se repite el mismo procedimiento con el punto B:

Al trazar una recta que une P con B, obtenemos el punto de intersección B' sobre el plano de proyección.

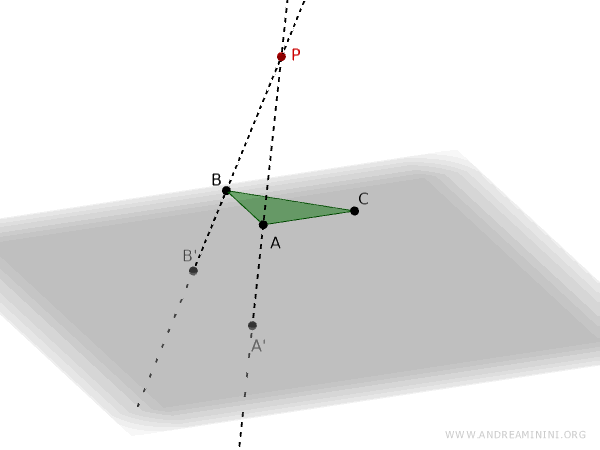
Por último, se traza una recta que une P con C, lo que nos permite determinar el punto C' en el plano.

Este procedimiento da lugar a la proyección del triángulo ABC sobre el plano q, tomando como centro de proyección el punto P.

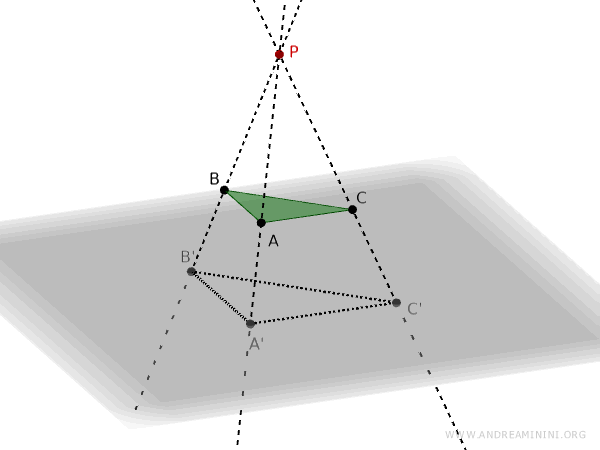
Al unir los puntos A', B' y C' en el plano, se obtiene la imagen proyectada del triángulo ABC.

El resultado final depende, naturalmente, de la forma del objeto (o del sólido), de la posición del punto de proyección P y de las características del plano (su distancia, inclinación, etc.).

A continuación se muestra otro ejemplo de proyección.

Sin embargo, ya es posible identificar ciertos invariantes. Por ejemplo: la proyección de un segmento sigue siendo un segmento; la proyección de una figura convexa conserva la convexidad; la proyección de un triángulo sigue siendo un triángulo. Estos son solo algunos de los invariantes que se pueden observar en el ejemplo analizado.

Y así sucesivamente.