Transformación geométrica identidad

La identidad es una transformación geométrica en la que cada punto del plano (o del espacio) se transforma en sí mismo, es decir, nada se desplaza ni se altera.

Es el tipo más elemental de transformación geométrica que existe.

Dicho de otro modo, es como decir: "Quiero transformar esta figura", pero sin realizar ninguna modificación. La figura permanece exactamente igual, sin traslaciones, rotaciones ni cambios de escala.

$$ \forall \ P \ \ ,\ \ P = f(P) $$

En términos matemáticos, equivale a multiplicar una figura por 1. Cualquier valor multiplicado por 1 permanece inalterado. $$ \forall \ x \ \ ,\ \ x = f(x \cdot 1) $$ En geometría, eso es precisamente lo que se entiende por identidad: una transformación que no modifica nada.

Un ejemplo práctico

Consideremos una figura geométrica, por ejemplo, un cuadrado.

Aplicamos ahora una rotación de 360° (una vuelta completa) a la figura.

El resultado es que todos los puntos permanecen en sus posiciones originales.

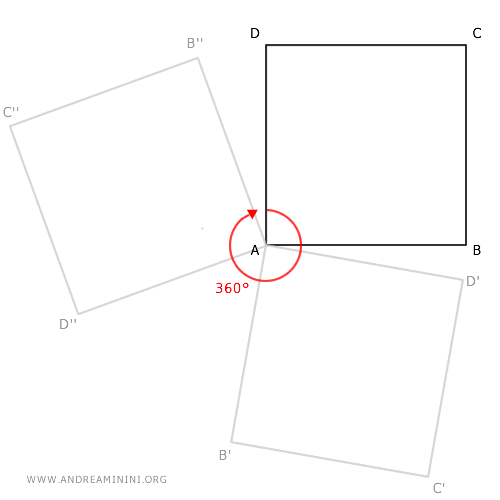
Tras la rotación completa, el punto B vuelve a ocupar exactamente las mismas coordenadas. Lo mismo sucede con los demás puntos.

$$ B = f(B)  $$

$$ C = f(C)  $$

$$ D = f(D)  $$

Este es un ejemplo clásico de una transformación identidad.

Otros ejemplos pueden ser dos vueltas completas (720°) o cualquier múltiplo de una rotación de 360°. También lo es una rotación de 0°. En todos estos casos, los puntos permanecen exactamente en el mismo lugar.

Y así sucesivamente.