Simetría axial

La simetría axial (también conocida como reflexión) es una transformación isométrica en la que cada punto de una figura se refleja con respecto a una recta, llamada eje de simetría, de manera que queda situado a la misma distancia pero en el lado opuesto.

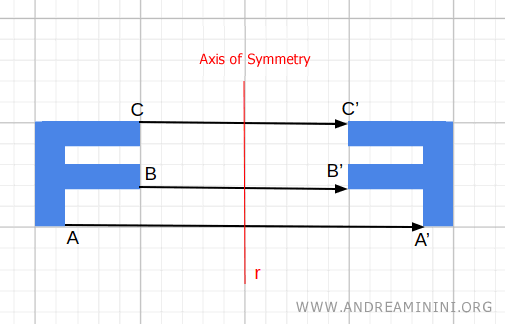
En términos generales, la simetría axial divide el plano en dos regiones mediante una recta r, denominada eje de simetría.

Para cada punto A ubicado en uno de los lados de la recta, existe un punto simétrico A' en el lado contrario.

El segmento que une A con A' es siempre perpendicular a la recta r y su punto medio se encuentra exactamente sobre el eje de simetría.

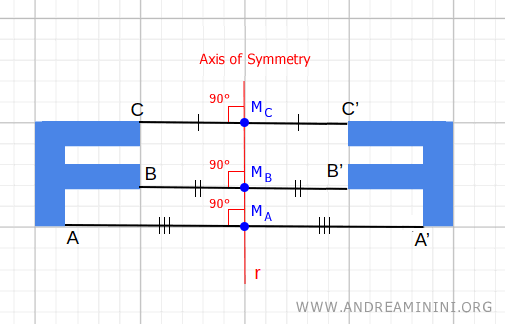
De ahí el nombre “axial”: la recta r actúa como eje del segmento que conecta los puntos A y A'.

• r es perpendicular al segmento AA'
• r pasa por el punto medio del segmento AA'

Nota: La simetría axial es una isometría porque refleja la figura de un semiplano al otro sin modificar su forma, tamaño ni las distancias entre puntos. Las figuras reflejadas son completamente congruentes.

Un ejemplo práctico

Por ejemplo, una figura ubicada en el semiplano izquierdo se refleja en el semiplano derecho, manteniéndose siempre perpendicular y equidistante respecto al eje de simetría r.

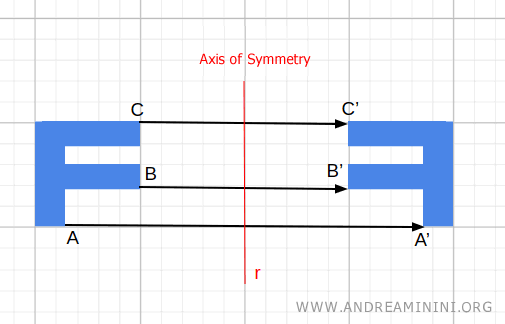
El punto C se refleja en el punto C', que se sitúa en el semiplano derecho.

Ambos puntos, C y C', se encuentran a 5 unidades del eje de simetría.

El segmento CC' tiene su punto medio sobre la recta r.

Definición formal de simetría axial

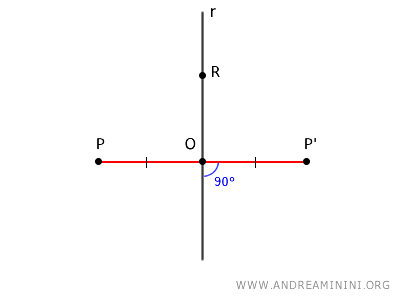
La recta r se denomina eje de simetría.

Por tanto, los segmentos OP y OP' son congruentes:

$$ \overline{OP} \cong \overline{OP'} $$

Todos los puntos R sobre la recta r permanecen invariantes, ya que su posición no cambia al aplicar la transformación.

Dicho de otro modo, todos los puntos de la recta r son puntos fijos de la simetría.

Tipos de simetría axial

Existen dos tipos principales de simetría axial:

• Reflexión
  Simetría axial dentro de un plano, es decir, una transformación en el espacio bidimensional.
• Volteo
  Simetría axial en el espacio tridimensional.

Simetrías axiales notables en geometría analítica

Algunas simetrías axiales son especialmente relevantes porque están definidas respecto a los ejes cartesianos, las bisectrices o rectas paralelas a los ejes del plano.

• Simetría respecto al eje x
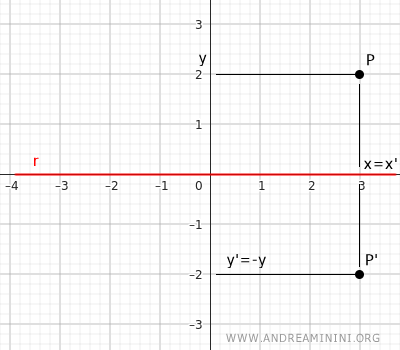
  En este caso, el eje de simetría es el eje x. Para calcular las coordenadas del punto simétrico P'(x';y') de un punto P(x;y), se aplican las siguientes fórmulas: $$ \begin{cases} x' = x \\ \\ y' = -y \end{cases} $$  Los puntos simétricos respecto al eje x comparten la misma coordenada x y tienen coordenadas y opuestas.

  Ejemplo: La componente x permanece inalterada, mientras que la y cambia de signo: y' = -y.
  

• Simetría respecto al eje y
  En este caso, el eje de simetría es el eje y del plano cartesiano. Las coordenadas del punto simétrico se obtienen con: $$ \begin{cases} x' = -x \\ \\ y' = y \end{cases} $$ Es decir, las coordenadas x se invierten y las y permanecen iguales.

  Ejemplo: La componente y no varía, pero la componente x cambia de signo.
  

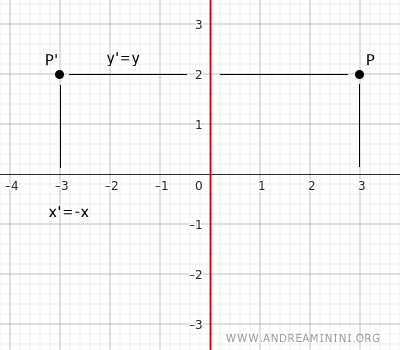
• Simetría respecto a una recta paralela al eje x
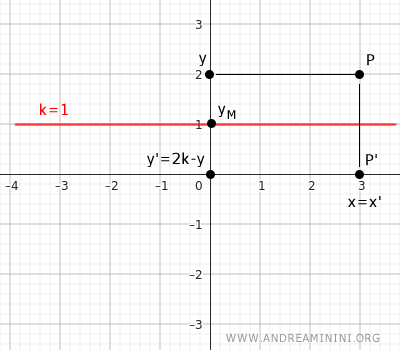
  Sea y=k una recta paralela al eje x. Las fórmulas de la transformación son: $$ \begin{cases} x' = x \\ \\ y' = 2k-y \end{cases} $$

  Demostración: La coordenada x se conserva, mientras que la coordenada y cambia. El punto medio y_M del segmento se calcula como: $$ k = \frac{y+y'}{2} $$ De donde se obtiene: $$ y' = 2k - y $$ Veamos un ejemplo práctico:
  

• Simetría respecto a una recta paralela al eje y
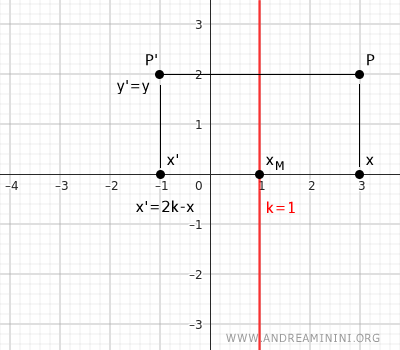
  Si el eje de simetría es una recta x=k paralela al eje y, las fórmulas correspondientes son: $$ \begin{cases} x' = 2k-x \\ \\ y' = y \end{cases} $$

  Demostración: La componente y se mantiene constante y la componente x se modifica. El punto medio M cumple: $$ k = \frac{x+x'}{2} $$ De ahí, se deduce: $$ x' = 2k - x $$ Observa este ejemplo:
  

• Simetría respecto a la bisectriz de los cuadrantes
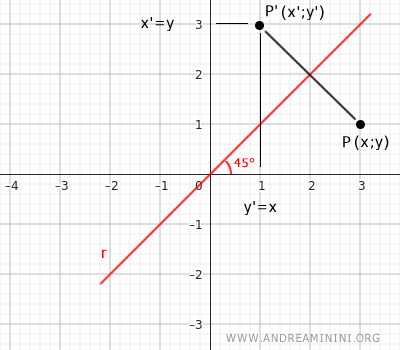
  La bisectriz de los cuadrantes puede actuar como eje de simetría. Si se trata de la bisectriz de los cuadrantes I y III, las fórmulas son: $$ \begin{cases} x' = y \\ \\ y' = x \end{cases} $$ Si es la bisectriz de los cuadrantes II y IV: $$ \begin{cases} x' = -y \\ \\ y' = -x \end{cases} $$

  Ejemplo: Aquí tienes una simetría respecto a la bisectriz del primer cuadrante: las coordenadas se intercambian.
  
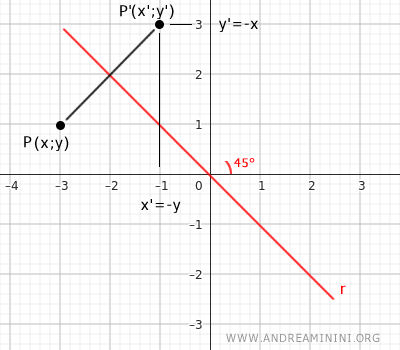
  En el siguiente caso, respecto a la bisectriz del segundo cuadrante, ambas coordenadas se invierten e intercambian de lugar.
  

• Reflexión respecto a una recta (y = mx + q)
  Para calcular la reflexión $P'(x', y')$ de un punto $P(x, y)$ respecto a una recta $r$ definida por la ecuación $ y = mx + q $, deben cumplirse dos condiciones esenciales:
  • Perpendicularidad
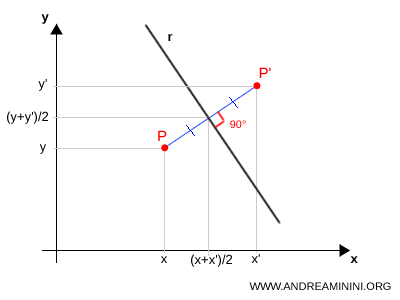    El segmento $PP'$ ha de ser perpendicular a la recta $r$. En consecuencia, la pendiente de $PP'$ es el recíproco negativo de $m$: $$ \frac{y' - y}{x' - x} = -\frac{1}{m} $$
  • Equidistancia
    El punto medio de $PP'$ debe encontrarse sobre la recta $r$. Es decir, el punto $$ M\!\left(\frac{x+x'}{2}, \; \frac{y+y'}{2}\right) $$ pertenece a $r$, lo que se traduce en la condición: $$ \frac{y+y'}{2} = m \cdot \frac{x+x'}{2} + q $$
  Al resolver este sistema en $x'$ y $y'$ se obtienen las coordenadas del punto reflejado: $$ \begin{cases} x' = \frac{(1-m^2)x + 2my - 2mq}{m^2+1} \\ \\ y' = \frac{(m^2-1)y + 2mx + 2q}{m^2+1} \end{cases} $$

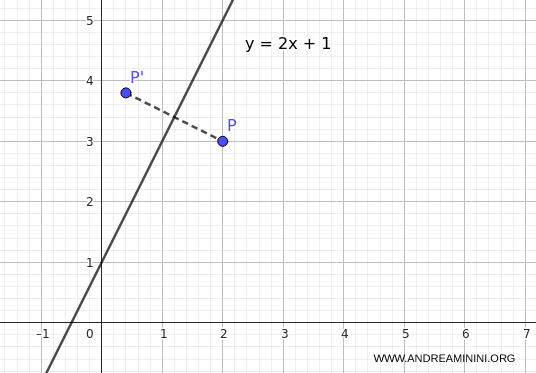
  Ejemplo. Calculemos la reflexión de $P(2,3)$ respecto a la recta $ r: \; y = 2x + 1 $. Aplicando las fórmulas de transformación: $$ \begin{cases} x' = \frac{(1-m^2)x + 2my - 2mq}{m^2+1} \\ \\ y' = \frac{(m^2-1)y + 2mx + 2q}{m^2+1} \end{cases} $$ Sustituyendo $m=2, q=1, x=2, y=3$: $$ \begin{cases} x' = \frac{(1-4)\cdot 2 + 2\cdot 2\cdot 3 - 2\cdot 2\cdot 1}{2^2+1} \\ \\ y' = \frac{(4-1)\cdot 3 + 2\cdot 2\cdot 2 + 2\cdot 1}{5} \end{cases} $$ $$ \begin{cases}
  x' = \frac{-6 + 12 - 4}{5} = \frac{2}{5} = 0.4 \\ \\ y' = \frac{9 + 8 + 2}{5} = \frac{19}{5} = 3.8 \end{cases} $$ Por lo tanto, la reflexión del punto $ P $ respecto a la recta $ r $ es $ P'(0.4,\;3.8) $.
  

• Simetría respecto de la recta (y = mx)
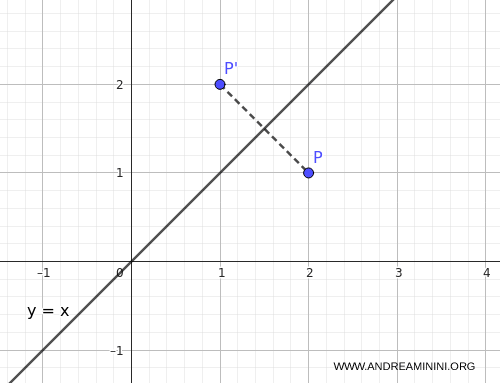
  Si el eje de simetría es la recta $ y = m x $ que pasa por el origen, las coordenadas del punto reflejado $(x',y')$ de un punto cualquiera $(x,y)$ se obtienen mediante las siguientes relaciones: $$ \begin{cases} x' = x \cos 2\alpha + y \sin 2\alpha \\[6pt] y' = x \sin 2\alpha - y \cos 2\alpha \end{cases} $$ donde $\alpha = \arctan(m)$ es el ángulo que forma la recta $y=mx$ con el eje $x$.

  Ejemplo. Determinar la simetría del punto $(2,1)$ respecto de la recta $y=x$. En este caso, la recta $y=x$ tiene pendiente $m=1$, por lo que $\alpha = \arctan(1) = \tfrac{\pi}{4}$. Al duplicar el ángulo se obtiene: $$ \cos 2\alpha = \cos \tfrac{\pi}{2} = 0, \qquad \sin 2\alpha = \sin \tfrac{\pi}{2} = 1 $$ Sustituyendo en la fórmula: $$ \begin{cases} x' = 2 \cdot 0 + 1 \cdot 1 = 1 \\[6pt] y' = 2 \cdot 1 - 1 \cdot 0 = 2 \end{cases} $$ Por lo tanto, la imagen simétrica de $(2,1)$ respecto de la recta $y=x$ es $(x',y') = (1,2)$.
  
  Demostración. Partimos de la fórmula general de la simetría respecto de la recta $ y=mx+q $: $$ \begin{cases} x' = \frac{(1-m^2)x + 2my - 2mq}{m^2+1} \\ \\ y' = \frac{(m^2-1)y + 2mx + 2q}{m^2+1} \end{cases} $$ Si la recta pasa por el origen ($q=0$), la expresión se simplifica a: $$ \begin{cases} x' = \frac{(1-m^2)x + 2my}{m^2+1} \\ \\ y' = \frac{(m^2-1)y + 2mx}{m^2+1} \end{cases} $$ Como $ m = \tan \alpha $, al sustituir obtenemos: $$ \begin{cases} x' = \frac{(1-\tan^2 \alpha)x + 2 \tan \alpha \, y}{1+\tan^2 \alpha} \\ \\ y' = \frac{(\tan^2 \alpha -1)y + 2 \tan \alpha \, x}{1+\tan^2 \alpha} \end{cases} $$ Simplificando resulta: $$ \begin{cases} x'= \frac{1-\tan^2 \alpha }{1+\tan^2 \alpha }\,x + \frac{2 \tan \alpha}{1+\tan^2 \alpha }\,y \\ \\ y'= \frac{2 \tan \alpha}{1+\tan^2 \alpha}\,x - \frac{1-\tan^2 \alpha}{1+\tan^2 \alpha}\,y \end{cases} $$ Finalmente, aplicando las identidades trigonométricas $ \cos 2 \alpha = \tfrac{1- \tan^2 \alpha}{1 + \tan^2 \alpha} $ y $ \sin 2 \alpha = \tfrac{2 \tan \alpha}{1 + \tan^2 \alpha} $, obtenemos: $$ \begin{cases} x'= x \cos 2 \alpha + y \sin 2 \alpha \\ \\ y'= x \sin 2 \alpha - y \cos 2 \alpha \end{cases} $$ con lo que queda demostrada la fórmula.

Estos son los casos más comunes de simetría axial en el plano.

También es posible calcular la reflexión respecto a una recta con inclinación arbitraria. En esos casos, sin embargo, se requiere el uso de la matriz de reflexión. Esto lo abordaremos en la próxima sección.

La matriz de reflexión

En el plano, la reflexión respecto a una recta y = mx (eje de simetría), que pasa por el origen del sistema cartesiano, puede expresarse mediante la matriz de reflexión.

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = A \cdot \begin{pmatrix} x \\ y \end{pmatrix} $$

Aquí, (x;y) representa las coordenadas originales de un punto P, mientras que (x';y') son las coordenadas del punto reflejado P'.

La matriz de reflexión viene dada por:

$$ A = \begin{pmatrix} \cos (2 \alpha) & \sin ( 2 \alpha ) \\ \sin ( 2 \alpha) & - \cos(2 \alpha) \end{pmatrix} $$

El ángulo α es el que forma la recta y = mx con el eje x positivo.

Nota: El ángulo α se puede calcular utilizando la arcotangente de la pendiente m de la recta y = mx, sabiendo que m = y/x. $$ \alpha = \arctan(m) $$ No obstante, esta fórmula no es aplicable cuando la recta r es perpendicular al eje x (90° o 270°), ya que en esos casos la pendiente tiende a infinito.

Para entender mejor su aplicación, veamos un ejemplo práctico.

Ejemplo

Consideremos el punto con coordenadas x = 2 e y = 3:

$$ P = (2;3) $$

Situamos el punto en el plano cartesiano:

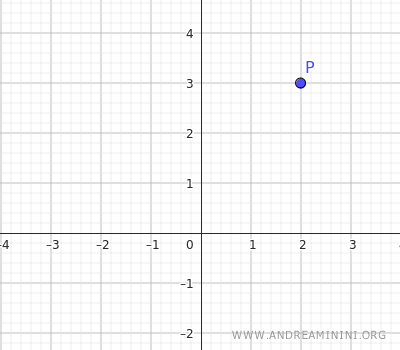
Para simplificar, tomamos como eje de simetría una recta y = mx que forma un ángulo de 90° (π/2 radianes) con el eje x positivo.

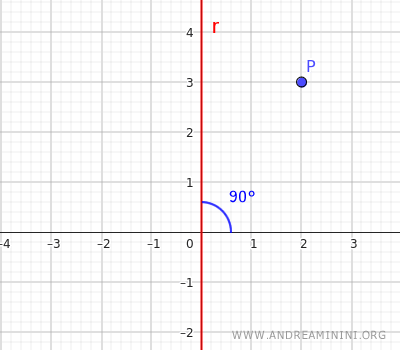
Calculamos las nuevas coordenadas mediante la matriz de reflexión:

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (2 \alpha) & \sin ( 2 \alpha ) \\ \sin ( 2 \alpha) & - \cos(2 \alpha) \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} $$

Las coordenadas del punto original son P = (2;3), es decir, x = 2 y y = 3.

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (2 \alpha) & \sin ( 2 \alpha ) \\ \sin ( 2 \alpha) & - \cos(2 \alpha) \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

En este caso, el ángulo es α = 90°, es decir, noventa grados (π/2 radianes).

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (2 \cdot 90°) & \sin (2 \cdot 90°) \\ \sin (2 \cdot 90°) & - \cos(2 \cdot 90°) \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos (180°) & \sin (180°) \\ \sin (180°) & - \cos(180°) \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

Sabemos que el seno de 180° es 0 y el coseno de 180° es -1:

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

$$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -2 \\ 3 \end{pmatrix} $$

Por lo tanto, las coordenadas del punto reflejado P' = (-2;3) son x = -2 y y = 3.

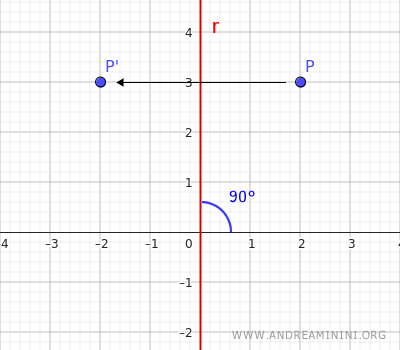
Simetría axial en el espacio con sólidos

La simetría axial en el espacio es una transformación geométrica que refleja un sólido respecto a un eje determinado.

Se trata de una isometría, por lo que conserva tanto las dimensiones como la forma del sólido original.

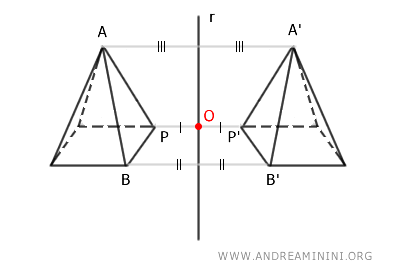
Dada una recta \( r \) en el espacio tridimensional, la simetría axial respecto a \( r \) se define de la siguiente manera:

1. Todos los puntos que pertenecen a la recta \( r \) permanecen fijos.
2. Cualquier otro punto \( P \) se transforma en un punto \( P' \) tal que:
   • El segmento \( PP' \) es perpendicular al eje \( r \).
   • Los puntos \( P \) y \( P' \) están a la misma distancia del eje \( r \). Es decir, los segmentos \( OP \cong OP' \), donde \( O \) es el punto de intersección entre el segmento \( PP' \) y la recta \( r \).

¿Cuáles son las propiedades de la simetría axial en el espacio?

Esta transformación conserva las distancias entre puntos: si dos puntos estaban separados por una distancia \( d \), esa misma distancia se mantiene tras la reflexión.

También se preservan el volumen, la forma del sólido y los ángulos entre sus caras.

En definitiva, el sólido reflejado es congruente con el original.

Simetría respecto a un plano

La simetría respecto a un plano es la versión tridimensional de la simetría axial. Mientras que en la simetría axial el eje es una recta, en este caso el elemento de simetría es un plano.

En este tipo de simetría, un punto y su imagen reflejada se encuentran a igual distancia del plano, alineados sobre una perpendicular al mismo.

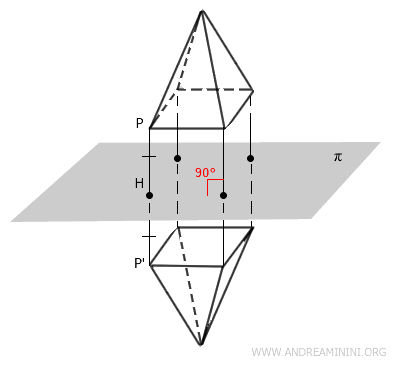
Sea una figura sólida en el espacio tridimensional y un plano de simetría \( \pi \):

1. Todo punto que se encuentre sobre el plano \( \pi \) permanece invariante.
2. Cualquier punto \( P \) que no esté sobre \( \pi \) se refleja en un punto \( P' \) tal que:
   - La recta \( PP' \) es perpendicular al plano \( \pi \).
   - Los segmentos \( PH \) y \( P'H \), donde \( H \) es la proyección ortogonal de \( P \) sobre el plano \( \pi \), son de igual longitud ( \( PH \cong P'H \) ).

Por tanto, el plano \( \pi \) actúa como plano de simetría.

Nota: En esta transformación, las figuras obtenidas por simetría respecto a un plano son imágenes especulares congruentes. Se preservan las distancias, los ángulos y las proporciones. Además, aplicar dos veces la simetría respecto a un mismo plano devuelve la figura original.

Observaciones

A continuación se presentan algunas observaciones adicionales sobre la simetría axial:

• La simetría axial es una isometría (demostración)
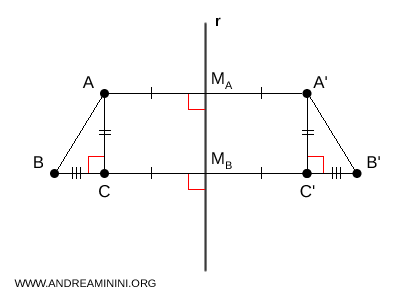
  Sea $A$ y $B$ dos puntos del plano. Al reflejarlos respecto de una recta $r$, obtenemos sus simétricos $A'$ y $B'$. Por definición, $A'$ y $B'$ se hallan a la misma distancia de $r$; además, las rectas $AA'$ y $BB'$ son perpendiculares a $r$, y los puntos $M_A$ y $M_B$, donde dichas rectas cortan a $r$, son los puntos medios de $AA'$ y $BB'$, respectivamente.
  
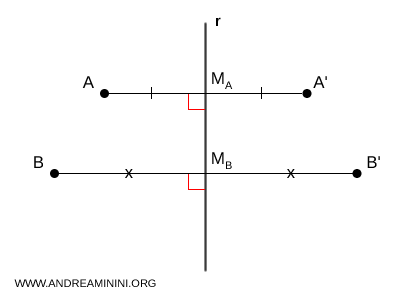
  Dado que $AA'$ y $BB'$ son perpendiculares a $r$, resulta que son paralelas: $ AA' \parallel BB' $. Por consiguiente, la distancia entre ellas es constante en todo punto. Sea $C$ la proyección ortogonal de $A$ sobre $BB'$, y $C'$ la de $A'$. Como $AA'$ y $BB'$ son paralelas, los segmentos $AC$ y $A'C'$ son perpendiculares a $BB'$, de modo que son paralelos y además congruentes: $AC \cong A'C'$.
  
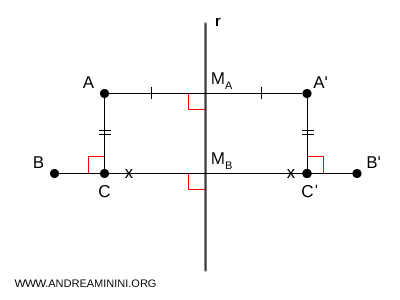
  Se deduce entonces que $AM_A$ y $CM_B$ son congruentes, ya que ambas representan la distancia de los puntos simétricos a la recta $r$, y la reflexión conserva dichas distancias. Del mismo modo, $A'M_A$ y $C'M_B$ resultan congruentes. De ello se infiere que $BC$ y $B'C'$ también son congruentes, $ BC \cong B'C' $, puesto que se obtienen como diferencias de segmentos congruentes ( $ BC = BM_B - CM_B $ y $ B'C' = B'M_B - C'M_B $ ).
  Finalmente, esto implica que $ AB \cong A'B' $, ya que los triángulos rectángulos $ ABC $ y $ A'B'C' $ son congruentes $ ABC \cong A'B'C' $. Comparten catetos congruentes ( $ BC \cong B'C' $ y $ AC \cong A'C' $ ), por lo cual sus hipotenusas también deben serlo $ AB \cong A'B' $. Así, queda demostrado que la simetría axial conserva la distancia entre puntos.
  
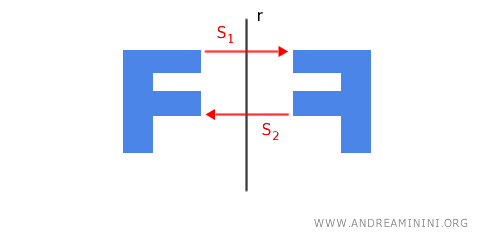
• La composición de dos simetrías axiales respecto al mismo eje equivale a la identidad
  Si se aplican dos simetrías axiales consecutivas S₁ y S₂ (o, en general, un número par de ellas) respecto al mismo eje r, la figura permanece inalterada. Es decir, se obtiene una transformación identidad, ya que todos los puntos regresan a su posición original. Por ello, una doble simetría axial con el mismo eje constituye una transformación involutiva.
  
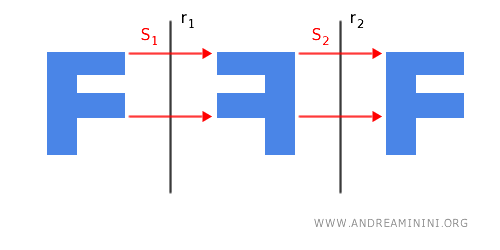
• La composición de dos simetrías axiales con ejes paralelos equivale a una traslación
  Cuando se aplican dos simetrías axiales S₁ y S₂ respecto a dos ejes paralelos r₁ y r₂, el resultado final es equivalente a una traslación de la figura original. La dirección y la magnitud del desplazamiento dependen de la distancia y orientación entre los ejes.
  

  Nota. El vector de traslación $\vec{v}$ tiene una magnitud igual al doble de la distancia ($d$) entre los dos ejes de simetría $r_1$ y $r_2$, y resulta perpendicular a ambos: $$ | \vec{v} | = 2d $$ Esto se deduce directamente de la figura.
  
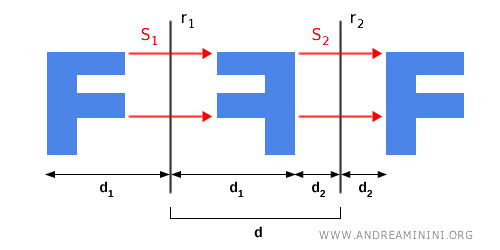
  Si sumamos los desplazamientos individuales obtenemos: $$ | \vec{v} | = 2d_1 + 2d_2 = 2(d_1 + d_2) $$ Como $d_1 + d_2 = d$, la distancia entre los dos ejes de simetría, llegamos finalmente a: $$ | \vec{v} | = 2(d_1 + d_2) = 2d $$

• La composición de dos simetrías axiales con ejes no paralelos equivale a una rotación
  Si las simetrías axiales S₁ y S₂ se realizan respecto a dos ejes no paralelos r₁ y r₂, el efecto global equivale a una rotación de la figura original. El centro de rotación se encuentra en el punto de intersección O de los ejes, y el ángulo de giro es el doble del ángulo formado entre ellos: 2α + 2β.
  
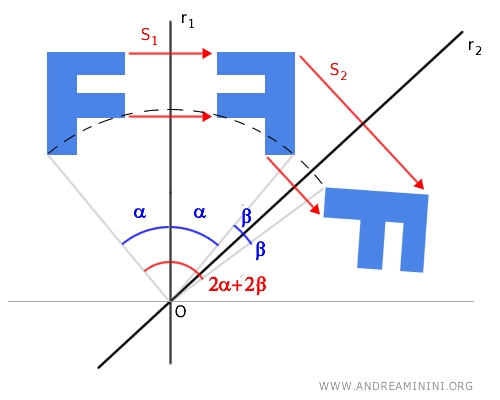
  Como el eje de simetría r₂ actúa como bisectriz del ángulo 2β = β₁ + β₂, con β₁ ≅ β₂, se deduce que los ángulos α + β₁ y α + β₂ también son congruentes. Denotamos este valor común como γ, por lo que γ ≅ α + β₁ ≅ α + β₂. Este ángulo γ coincide con el formado por los ejes r₁ y r₂. Por tanto, el ángulo de rotación puede calcularse simplemente como el doble del ángulo γ.
  

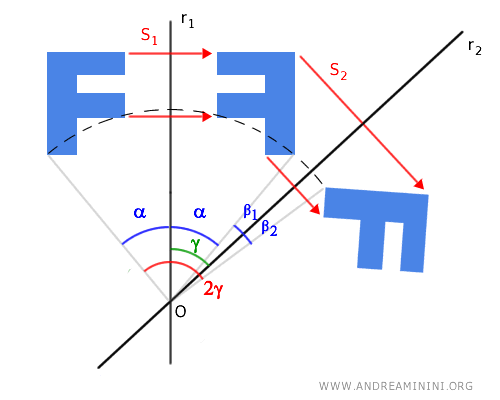
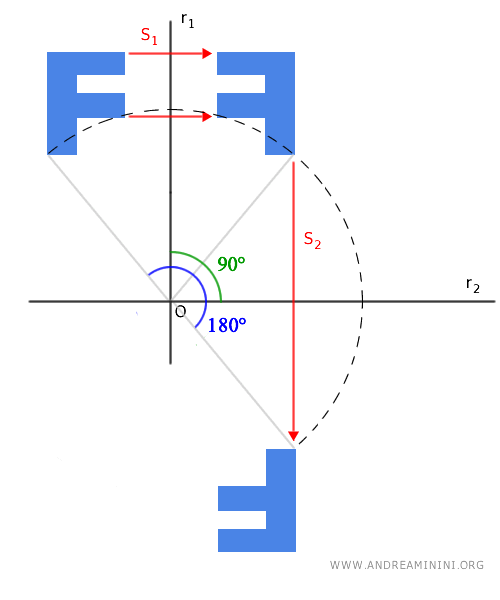
  Nota: Si los ejes de simetría r₁ y r₂ son perpendiculares y forman un ángulo recto (90°), entonces la composición equivale a una rotación de 180° (media vuelta).
  

• Toda isometría puede descomponerse en simetrías axiales
  Este resultado se fundamenta en propiedades fundamentales ya establecidas. En particular:
  • Las rotaciones, las identidades y las traslaciones pueden expresarse como composiciones de dos simetrías axiales bien elegidas. 
  • Las simetrías centrales son equivalentes a una rotación de 180 grados en torno a un punto P.
    
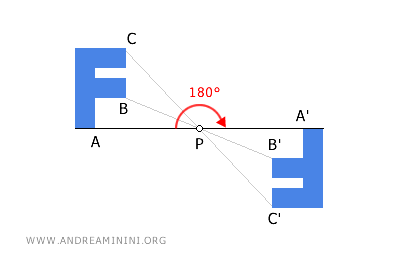
    Dado que cualquier rotación puede representarse mediante simetrías axiales, también es posible obtener la simetría central como composición de simetrías axiales.
  En consecuencia, toda isometría del plano puede construirse mediante una combinación adecuada de simetrías axiales.
• Figuras invariantes en la simetría axial
  En una simetría axial, el eje de simetría $(r)$ es una figura invariante porque no se modifica. De manera más precisa, se trata de una figura puntualmente invariante, ya que cada uno de sus puntos conserva exactamente las mismas coordenadas tras la transformación.
  
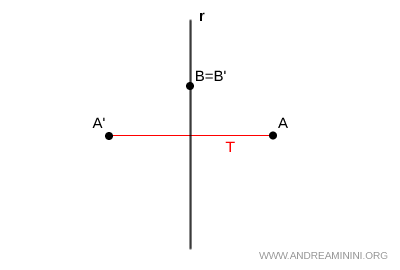
  Asimismo, cualquier recta perpendicular al eje de simetría también resulta invariante. En este caso, sin embargo, hablamos de invariancia global: la recta en su conjunto permanece idéntica, aunque los puntos que la componen se trasladan a posiciones diferentes bajo la simetría.
  

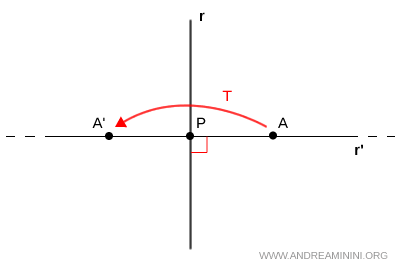
  Nota. La recta $r'$ se conserva tras la transformación, aunque cada punto se desplace a un lugar distinto. Por ejemplo, el punto $A$ se transforma en $A'$.

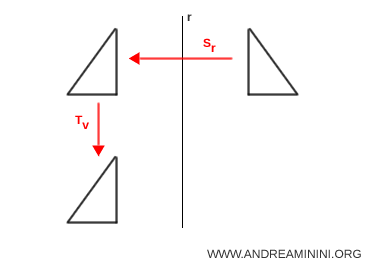
• Reflexión deslizante
  Una reflexión deslizante es la composición de una reflexión con una traslación, en la que el vector de traslación es paralelo al eje de reflexión.
  

Y así sucesivamente.