Transformaciones involutivas en geometría
Una transformación involutiva en geometría (o involución) es aquella transformación que, al aplicarse dos veces consecutivas, restituye el objeto a su estado original, comportándose efectivamente como una transformación identidad.
En otras palabras, se trata de una transformación \( T \) que, al actuarse dos veces sobre una figura geométrica (como una figura plana, un cuerpo sólido, etc.), la devuelve exactamente a su posición inicial.
Desde el punto de vista formal, una transformación involutiva se define como una función que, aplicada dos veces a cualquier punto \( x \), devuelve ese mismo punto:
$$ T(T(x)) = x $$
Las transformaciones involutivas están presentes en distintas ramas de la geometría - como la euclídea, la proyectiva o la algebraica - y presentan propiedades notables desde el punto de vista tanto geométrico como algebraico.
A continuación, se presentan algunos ejemplos típicos de transformaciones geométricas involutivas:
- Reflexión (simetría axial)
La reflexión de una figura respecto a una recta (en el plano) o respecto a un plano (en el espacio tridimensional) constituye un ejemplo clásico de transformación involutiva. Si se aplica dos veces una misma reflexión, cada punto de la figura vuelve exactamente a su posición original.

- Simetría central
La simetría respecto a un punto (también llamada simetría central) es otro caso característico de transformación involutiva. Al aplicarla dos veces sobre un mismo punto, se obtiene de nuevo el punto de partida.

Transformaciones involutivas en geometría analítica
Una transformación \( t \) se denomina involutiva cuando coincide con su propia inversa: \( t = t^{-1} \).
En otras palabras, aplicar la transformación dos veces consecutivas equivale a efectuar la transformación identidad, que no altera ningún punto del plano.
$$t \circ t = i $$
Aquí, \( i \) representa la transformación identidad.
Esta propiedad implica que la transformación se revierte a sí misma: \( t \circ t = i \Leftrightarrow t = t^{-1} \).
Ejemplo
Consideremos la transformación \( t \) definida por el siguiente sistema de ecuaciones:
$$ t: \begin{cases} x' = -x \\ \\ y' = -y \end{cases} $$
Dicha transformación asocia a cada punto \( P(x, y) \) su simétrico respecto al origen, es decir, \( P'(-x, -y) \).
Al aplicar nuevamente la transformación, se obtiene:
- \( P(x, y) \mapsto P'(-x, -y) \)
- \( P'(-x, -y) \mapsto P''(x, y) = P \)
Por lo tanto, \( t \circ t = i \): la transformación \( t \) es involutiva, ya que restituye cada punto a su posición original.
Por ejemplo, al aplicar \( t \) al punto \( P(1, 2) \), se obtiene:
- \( P(1, 2) \mapsto P'(-1, -2) \)
- \( P'(-1, -2) \mapsto P''(1, 2) \)
El punto final \( P'' \) coincide exactamente con el punto inicial \( P(1, 2) \).
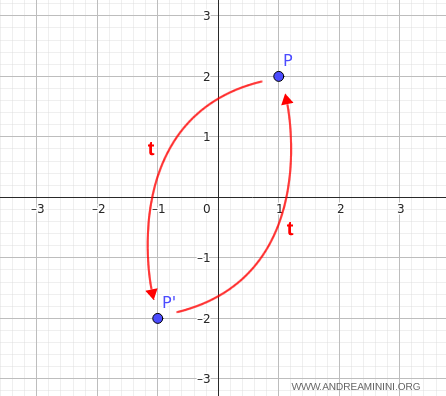
En resumen, aplicar esta transformación dos veces equivale a no haberla aplicado en absoluto.
Y así sucesivamente.