Líneas de simetría

Las líneas de simetría son líneas imaginarias que dividen una figura geométrica en dos partes iguales, como reflejadas en un espejo.

La cantidad y disposición de estas líneas varía según la forma de la figura.

Algunas figuras geométricas presentan una o varias líneas de simetría. A continuación se muestran algunos ejemplos representativos:

• Triángulo isósceles
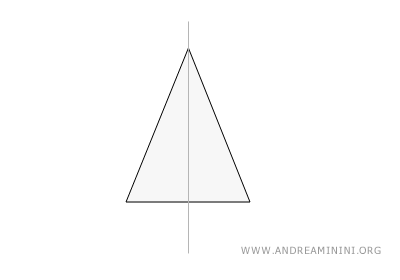
  Este triángulo tiene dos lados iguales y una única línea de simetría que va desde el vértice opuesto a la base, dividiéndolo en dos mitades idénticas. Por ello, posee solo una línea de simetría.
  
• Triángulo equilátero
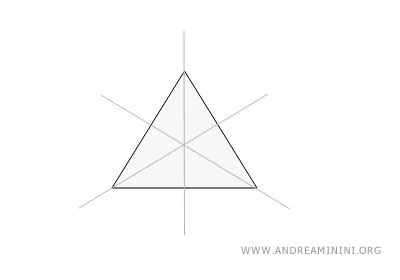
  En esta figura, todos los lados y ángulos son congruentes. Cuenta con tres líneas de simetría, cada una trazada desde un vértice hasta el punto medio del lado opuesto, dividiendo el triángulo en dos partes iguales.
  
• Triángulo escaleno
  Como no tiene lados ni ángulos iguales, este triángulo no posee ninguna línea de simetría.
• Cuadrado
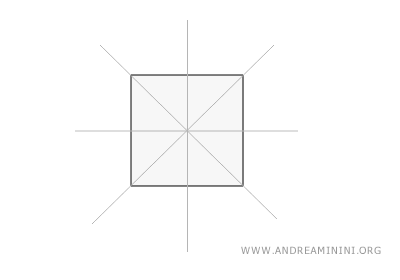
  El cuadrado presenta cuatro lados iguales y ángulos rectos. Tiene cuatro líneas de simetría: dos diagonales que unen vértices opuestos y dos líneas que pasan por los puntos medios de lados enfrentados.
  
• Rectángulo
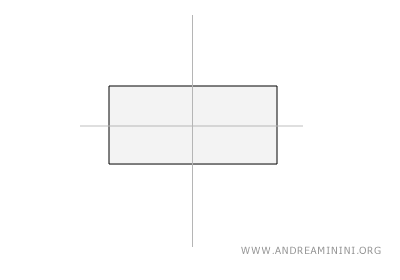
  Un rectángulo tiene dos líneas de simetría, ambas trazadas entre los puntos medios de lados opuestos.
  
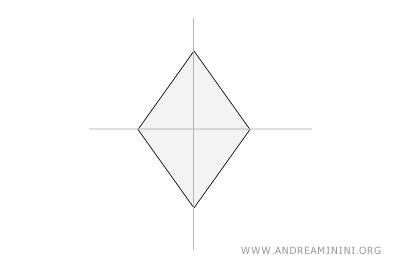
• Rombo
  Esta figura tiene cuatro lados iguales, aunque no necesariamente ángulos rectos. Posee dos líneas de simetría que conectan pares de vértices opuestos.
  
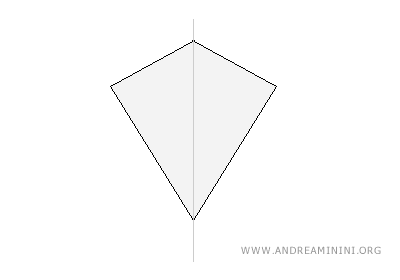
• Cometa
  El cometa (o papalote) presenta una sola línea de simetría: su diagonal más larga. Esta línea divide la figura en dos mitades simétricas y parte por la mitad el ángulo formado entre los lados iguales.
  
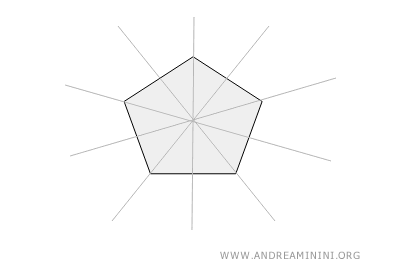
• Pentágono regular
  Con cinco lados y ángulos iguales, el pentágono regular tiene cinco líneas de simetría. Cada una atraviesa un vértice y el punto medio del lado opuesto, dividiendo la figura en dos partes simétricas.
  
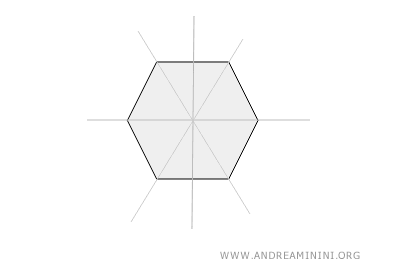
• Hexágono regular
  Un hexágono regular, con seis lados y ángulos iguales, posee seis líneas de simetría. Cada línea pasa por un vértice y el centro del lado opuesto, dividiendo la figura en mitades iguales.
  
• Círculo
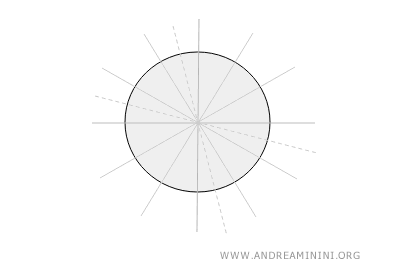
  El círculo es completamente simétrico, con infinitas líneas de simetría. Cualquier diámetro puede considerarse una línea de simetría.
  

Notas

Algunas observaciones adicionales sobre las líneas de simetría:

• Una línea se considera línea de simetría si la simetría axial respecto a dicha línea genera una figura invariante.

  Aquí, una "figura unificada" se refiere a una figura que coincide exactamente con su imagen tras una transformación geométrica, en este caso, una simetría axial.

Y así sucesivamente.