Homotecia

La homotecia es una transformación geométrica que traslada los puntos de una figura con respecto a un punto fijo O, modificando sus distancias de manera proporcional según un factor k, pero conservando inalterada la forma de la figura.
an example of direct homothety
El punto O se denomina centro de homotecia, y el número k recibe el nombre de razón de homotecia.

Homotecia directa e inversa
Un ejemplo práctico
Ecuaciones de la homotecia
Homotecia en el espacio tridimensional
Observaciones clave

Homotecia directa e inversa

Dicho con otras palabras, una homotecia puede ampliar o reducir una figura, manteniendo la alineación de los puntos (colinealidad) y las proporciones entre ellos.

Por ejemplo, tomemos una figura ABC y elijamos el punto O como centro de homotecia, asignando un valor k a la razón de homotecia.

the center of homothety

Si consideramos el vector $ \overrightarrow{OA} $ y lo multiplicamos por el factor k, obtenemos un nuevo vector $ \overrightarrow{OA'} $ con el mismo origen y dirección que el inicial, pero de longitud distinta.

$$ \overrightarrow{OA'} = k \times \overrightarrow{OA} $$

Esto nos permite determinar un nuevo punto A' sobre la misma recta que une O con A.

an example of direct homothety

Así, si A es un punto de la figura original y A' su correspondiente en la figura homotética, los puntos O, A y A' están alineados, y el segmento OA' mide k veces lo que mide el segmento OA.

Nota: Utilizo vectores (como $ \overrightarrow{OA} $) en lugar de segmentos (como $ \overline{OA} $) porque en una homotecia es esencial tener en cuenta la dirección de la transformación. Esto se debe a que la razón k puede ser negativa (k<0), lo que indica una “homotecia inversa”.

Si repetimos este procedimiento con los demás puntos B y C de la figura original, obtendremos una nueva figura A'B'C', semejante a la inicial.

La figura A'B'C' mantiene la misma forma que la figura ABC, pero cambia de tamaño.

En este caso, la figura resultante es una ampliación.

an example of direct homothety

Dependiendo del valor del factor k, se pueden observar distintos efectos:

Si |k| > 1, la homotecia produce una ampliación.
Si |k| < 1, produce una reducción.
Si k = 1, la homotecia equivale a una transformación identidad, es decir, la figura no se modifica.
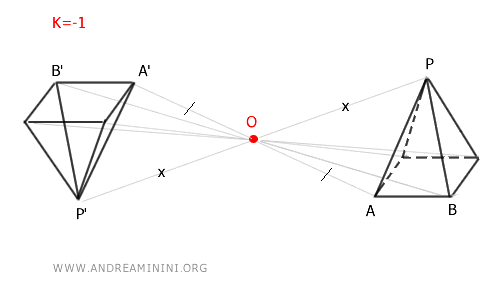
Si k = -1, la homotecia equivale a una simetría central.

Es importante tener presente que la razón de homotecia también puede ser negativa (k<0).

El signo de k determina el tipo de homotecia: directa o inversa.

Homotecia directa
Cuando k > 0, hablamos de homotecia directa, ya que los puntos correspondientes permanecen en el mismo cuadrante.
Homotecia inversa
Cuando k < 0, se trata de una homotecia inversa, que no solo amplía o reduce, sino que además genera una simetría respecto al centro O.

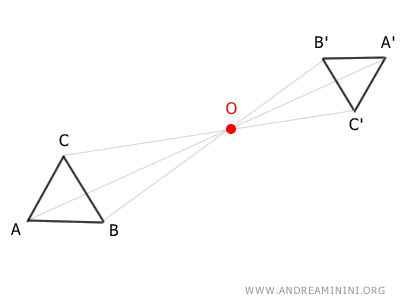
¿Para qué se utiliza? La homotecia permite ampliar o reducir figuras geométricas manteniendo su forma y proporciones. Es especialmente útil para estudiar las relaciones entre figuras semejantes.

Un ejemplo práctico

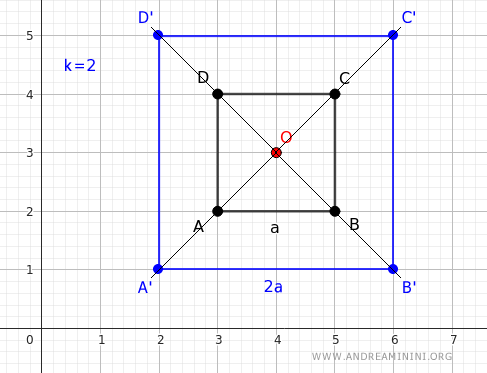
Supongamos un cuadrado de lado a cuyo centro coincide con el centro de homotecia O.

example

Si aplicamos una homotecia con razón k=2, obtenemos un cuadrado con lado 2a.

El resultado es una ampliación.

example of enlargement

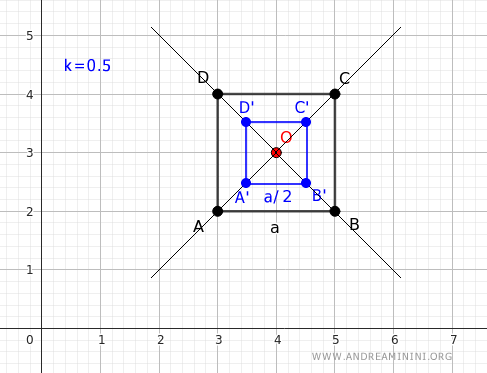
Si aplicamos una homotecia con razón k = 0.5, el cuadrado resultante tendrá lado a/2.

En este caso, se trata de una reducción.

an example of reduction

Como es evidente, el resultado también depende del centro de homotecia elegido, aunque la razón k sea la misma.

Por ejemplo, si tomamos el mismo cuadrado pero con centro en O(2,3):

an example of a square

Aplicando una homotecia con k=2, el nuevo cuadrado tendrá lado 2a.

an example of enlargement

El resultado es completamente distinto al del caso anterior.

Ecuaciones de la homotecia

Estas ecuaciones permiten describir la homotecia en coordenadas cartesianas cuando el centro O se encuentra en el origen del plano, es decir, en O(0,0).

$$ \begin{cases} x' = k \cdot x \\ \\ y' = k \cdot y \end{cases} $$

Aquí, k es la razón de homotecia, (x, y) son las coordenadas de un punto en la figura original, y (x', y') las de su imagen en la figura homotética.

Por lo tanto, las ecuaciones de la homotecia inversa son:

$$ \begin{cases} x = \dfrac{1}{k} \cdot x' \\ \\ y = \dfrac{1}{k} \cdot y' \end{cases} $$

Si el centro O no está en el origen, sino en un punto cualquiera O(x₀, y₀), las ecuaciones cambian ligeramente:

$$ \begin{cases} x' = x_0 + k \cdot (x - x_0) \\ \\ y' = y_0 + k \cdot (y - y_0) \end{cases} $$

Estas expresiones indican cómo se transforma cada punto de la figura original respecto al centro O(x₀, y₀).

Ejemplo: En este caso, la razón es k=2 y el centro de homotecia se encuentra en las coordenadas O(2,3), por lo tanto x₀=2 e y₀=3.
an example of enlargement
El punto A se encuentra en (x, y) = (3, 2). Aplicamos las ecuaciones para calcular su imagen A': $$ \begin{cases} x' = x_0 + k \cdot (x - x_0) \\ \\ y' = y_0 + k \cdot (y - y_0) \end{cases} $$ Sustituimos k=2: $$ \begin{cases} x' = x_0 + 2 \cdot (x - 2) \\ \\ y' = y_0 + 2 \cdot (y - 3) \end{cases} $$ Sustituyendo x₀=2 e y₀=3: $$ \begin{cases} x' = 2 + 2 \cdot (x - 2) \\ \\ y' = 3 + 2 \cdot (y - 3) \end{cases} $$ Usamos las coordenadas de A (x=3, y=2): $$ \begin{cases} x' = 2 + 2 \cdot (1) \\ \\ y' = 3 + 2 \cdot (-1) \end{cases} $$ $$ \begin{cases} x' = 4 \\ \\ y' = 1 \end{cases} $$ Por tanto, la imagen A' tiene coordenadas x'=4 e y'=1. $$ \begin{cases} x' = 4 \\ \\ y' = 1 \end{cases} $$ Aplicando el mismo procedimiento, podemos obtener las imágenes de los puntos B', C' y D'.

Homotecia en el espacio tridimensional

La homotecia en el espacio tridimensional es una transformación geométrica que modifica el tamaño de las figuras - ya sea ampliándolas o reduciéndolas - preservando sus proporciones con respecto a un punto fijo llamado centro de homotecia. Esta transformación mantiene la razón entre las distancias, de modo que la figura resultante es siempre semejante a la original.

Se trata de una generalización del concepto de homotecia en el plano, aplicada ahora a los tres ejes del espacio, afectando a todos los puntos que lo componen.

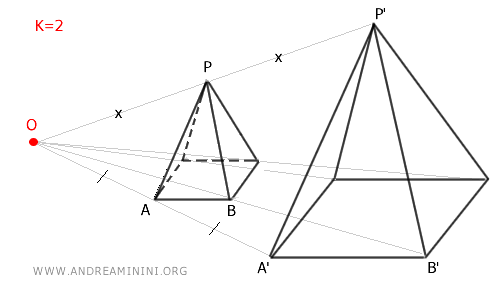
example

Sea $ O $ un punto fijo en el espacio y $ k \neq 0 $ un número real denominado razón de homotecia.

Una homotecia de centro $ O $ y razón $ k $ transforma cada punto $ P(x, y, z) $ en un nuevo punto $ P'(x', y', z') $, según la fórmula:

\[ P' = O + k (P - O) \]

En coordenadas, si $ O(x_0, y_0, z_0) $ y $ P(x, y, z) $, entonces el punto transformado $ P'(x', y', z') $ se obtiene mediante:

\[ x' = x_0 + k (x - x_0) \]

\[ y' = y_0 + k (y - y_0) \]

\[ z' = z_0 + k (z - z_0) \]

En términos sencillos, cada punto $ P $ se desplaza a lo largo de la recta que une $ O $ y $ P $, multiplicando su distancia al centro $ O $ por el factor $ k $.

Homotecia directa e inversa

En el espacio, la homotecia puede clasificarse como directa o inversa, dependiendo del signo del valor de $ k $.

Homotecia directa
Cuando $ k > 0 $, la transformación es directa: los puntos se alejan o se acercan radialmente al centro $ O $, sin modificar la orientación de la figura. Si $ k > 1 $, se produce una ampliación; si $ 0 < k < 1 $, una reducción. Por ejemplo, con $ k = 2 $, el sólido resultante tiene el doble de tamaño. En el caso $ k = 1 $, la transformación no altera la figura original.
Homotecia inversa
Cuando $ k < 0 $, se trata de una homotecia inversa: los puntos se reflejan con respecto al centro $ O $, situándose en el lado opuesto de la recta $ OP $, invirtiendo así la orientación del objeto. En particular, si $ k = -1 $, se obtiene una simetría central respecto de $ O $, que conserva la forma y el tamaño de la figura, pero con orientación opuesta.

Ejemplo 1

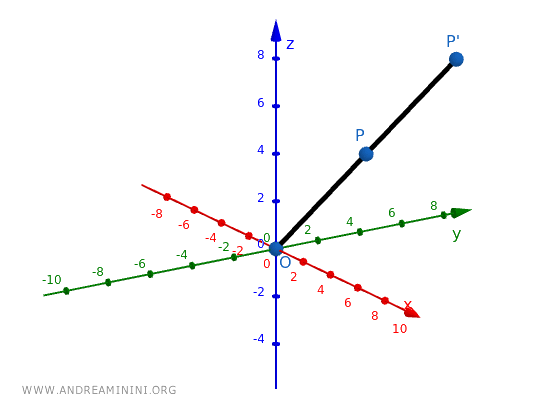
Una homotecia directa con $ k = 2 $, aplicada a un cubo centrado en $ O $, duplica sus dimensiones sin alterar ni su forma ni su orientación.

Consideramos el punto $ P(2, 3, 4) $ y aplicamos una homotecia de centro $ O(0, 0, 0) $ con $ k = 2 $:

\[ x' = 0 + 2(2 - 0) = 4 \]

\[ y' = 0 + 2(3 - 0) = 6 \]

\[ z' = 0 + 2(4 - 0) = 8 \]

El punto transformado es $ P'(4, 6, 8) $, que se encuentra sobre la misma recta que une $ O $ con $ P $, pero al doble de distancia.

example of direct homothety

Ejemplo 2

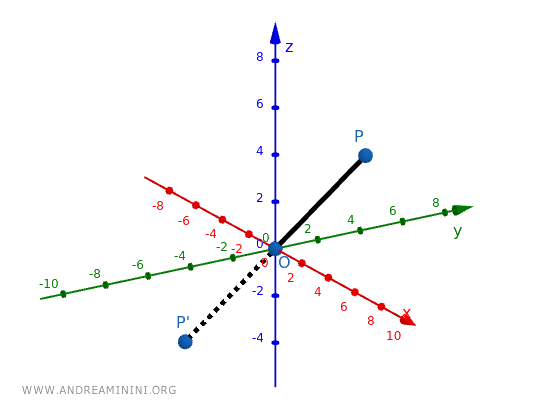
En una homotecia inversa, la figura resultante se refleja respecto al centro $ O $, invirtiendo su orientación espacial. Si aplicamos una homotecia con $ k = -1 $ a un cubo, este queda invertido respecto de $ O $.

Partimos nuevamente del punto $ P(2, 3, 4) $ y aplicamos la transformación con $ k = -1 $:

\[ x' = 0 + (-1)(2 - 0) = -2 \]

\[ y' = 0 + (-1)(3 - 0) = -3 \]

\[ z' = 0 + (-1)(4 - 0) = -4 \]

El nuevo punto es $ P'(-2, -3, -4) $, que corresponde al reflejo de $ P $ respecto al punto $ O $.

En resumen, la homotecia directa conserva la orientación de la figura, mientras que la inversa la invierte.

inverse homothety

Propiedades fundamentales de la homotecia en el espacio

Entre las principales propiedades de la homotecia en el espacio tridimensional, destacan las siguientes:

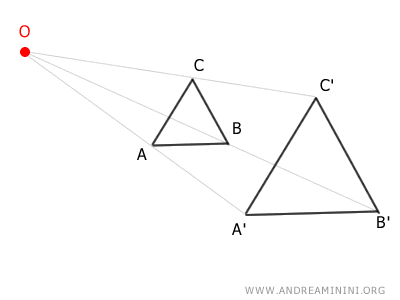
Semejanza: Las figuras homotéticas son siempre semejantes a las originales, es decir, mantienen las mismas proporciones entre sus partes.
Colinealidad: Si tres puntos eran colineales antes de la transformación, seguirán siéndolo después.
Paralelismo: Los planos paralelos permanecen paralelos tras la homotecia.
Escalado de áreas y volúmenes:
- Si una figura tiene área $ A $, tras aplicar una homotecia con razón $ k $, su nueva área será $ A' = k^2 A $.
- Si su volumen es $ V $, el volumen transformado será $ V' = k^3 V $.

Observaciones clave

A continuación, se recogen algunas observaciones esenciales sobre la homotecia:

La homotecia no es una isometría
Dado que modifica las distancias absolutas entre los puntos (excepto cuando $ k = 1 $), no se considera una transformación isométrica. Sin embargo, al igual que las isometrías, conserva propiedades invariantes como la amplitud de los ángulos, la colinealidad y las proporciones relativas entre segmentos.

Propiedades esenciales de una homotecia:
- Una homotecia transforma siempre un segmento en otro de longitud proporcional al original.
- Preserva íntegramente la medida de los ángulos.
- El centro de la homotecia es el único punto que permanece fijo bajo la transformación.
- Toda recta que pasa por el centro se mantiene invariante como conjunto.
Proporcionalidad de distancias
Las distancias en la figura transformada son proporcionales a las distancias correspondientes en la figura original. Es decir, las relaciones entre longitudes se mantienen, aunque las medidas absolutas cambien.

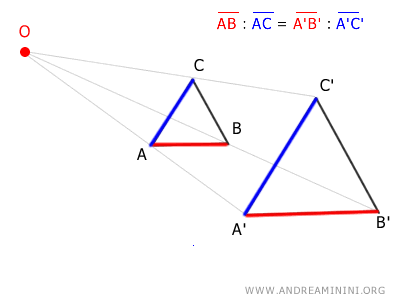
Por ejemplo, el segmento AB guarda la misma proporción con AC que su imagen A'B' con A'C': $$ \overline{AB}:\overline{AC} = \overline{A'B'}: \overline{A'C'} $$
Conservación de los ángulos
Los ángulos de la figura original y los de la figura transformada son congruentes, es decir, conservan exactamente la misma medida.
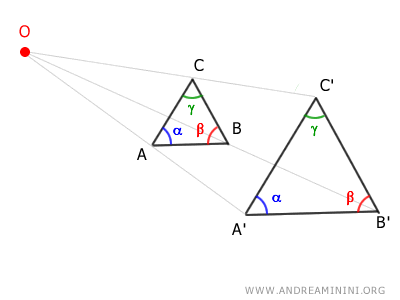
Invariancia del centro
El centro de homotecia, $ O $, permanece fijo durante toda la transformación y constituye el único punto invariante de la figura.
Cuando $ k = -1 $, la homotecia equivale a una simetría central
En este caso particular, los vectores de transformación conservan origen y dirección, pero con sentido opuesto. El efecto final coincide exactamente con el de una simetría central respecto al mismo centro $ O $.

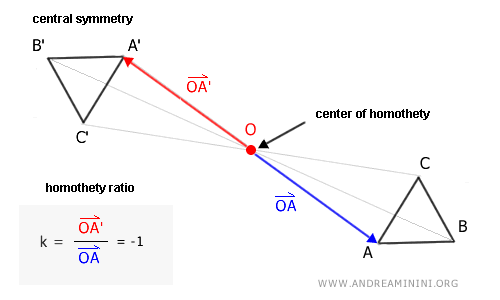
Nota: En este caso, los lados de la figura original y los de la figura transformada son congruentes: $$ \overline{AB} \cong \overline{A'B'} \\ \overline{AC} \cong \overline{A'C'} \\ \overline{BC} \cong \overline{B'C'} $$
La composición de dos homotecias con el mismo centro es, a su vez, una homotecia con ese mismo centro
Cuando dos homotecias $ T_1 $ y $ T_2 $ tienen el mismo centro $ O $, su composición vuelve a ser una homotecia centrada en $ O $, cuyo factor de escala es el producto de los dos coeficientes: $ k = k_1 \cdot k_2 $.
En efecto, si $$ T_1 : \begin{cases} x' = k_1 x \\ \\
y' = k_1 y \end{cases} \quad\text{y}\quad T_2 : \begin{cases} x' = k_2 x \\ \\ y' = k_2 y \end{cases} $$ entonces su composición $ T_1 \circ T_2 $ se obtiene como: $$ T_1 \circ T_2 : \begin{cases} x' = k_1 (k_2 x) = (k_1 k_2)x \\ \\ y' = k_1 (k_2 y) = (k_1 k_2)y \end{cases} $$ De modo que $$ T_1 \circ T_2 = H(O, k_1 k_2) $$ es decir, el resultado es una homotecia con centro en $ O $ y razón de escala $ k = k_1 k_2 $.
Nota. Todas las homotecias que comparten un mismo centro forman un grupo respecto a la operación de composición, ya que cumplen las propiedades fundamentales de un grupo:
- Cierre: la composición de dos homotecias sigue siendo una homotecia con el mismo centro.
- Asociatividad: la composición de transformaciones es asociativa por definición.
- Elemento neutro: existe una homotecia identidad ($ k = 1 $) que deja invariados todos los puntos.
- Elemento inverso: toda homotecia con razón $ k $ tiene una homotecia inversa con razón $ k^{-1} = \frac{1}{k} $.

Y así sucesivamente.