Simetría central

La simetría central es una transformación geométrica que asocia a cada punto A de una figura otro punto A' con respecto a un punto fijo P, denominado centro de simetría. Esta transformación se define de modo que P sea el punto medio del segmento que une A con A'.

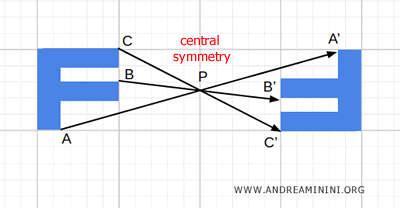
La simetría central es una isometría, ya que conserva inalteradas las distancias entre los puntos de la figura.

El centro de simetría $ P $ es el punto fijo de la transformación.

Esta transformación puede aplicarse tanto en el plano como en el espacio euclídeo tridimensional.

En el plano, la simetría central puede interpretarse como una rotación de 180° alrededor del centro de simetría. En el espacio tridimensional, actúa como una isometría inversa.

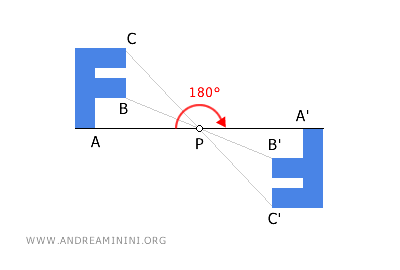
Un ejemplo práctico

La simetría central es una transformación geométrica definida con respecto a un punto fijo, denominado centro de simetría.

Dicho punto, que denotamos con P, actúa como referencia para toda la transformación.

Imaginemos, por ejemplo, una figura trazada en el plano y seleccionamos un punto fijo P como centro de simetría.

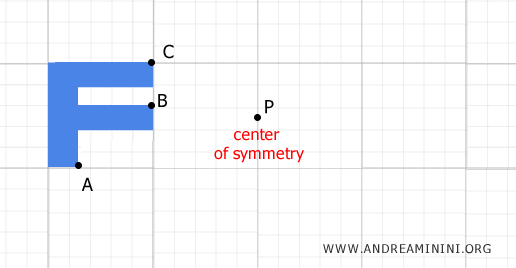
Consideramos ahora los puntos A, B y C de la figura.

Luego, trazamos semirrectas desde cada uno de estos puntos (A, B y C) que pasen por el centro de simetría P.

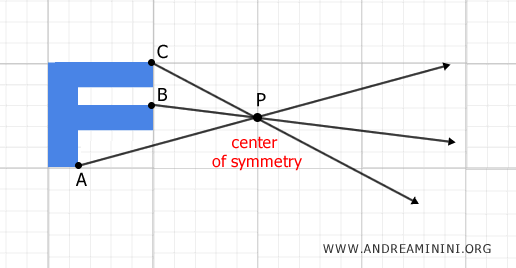
De este modo, cada punto de la figura se transforma en su simétrico, de manera que P queda ubicado exactamente en el punto medio del segmento que los une.

Tomemos, por ejemplo, el punto A. El punto A' se encuentra sobre la misma recta que pasa por P y A, a igual distancia de P que A, pero en sentido opuesto.

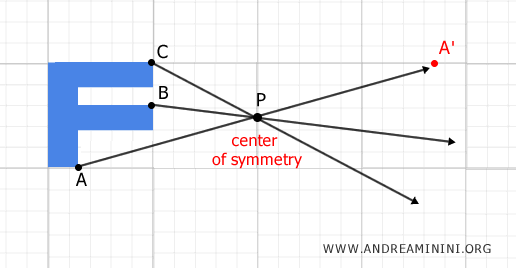
Los puntos A y A' se denominan puntos simétricos con respecto al punto P.

El centro de simetría P es el punto medio del segmento AA'. Es decir, P divide al segmento AA' en dos partes congruentes.

$$ \overline{AP} \cong \overline {A'P} $$

Al repetir este proceso para todos los puntos de la figura, se obtiene una imagen rotada 180° con respecto al punto P.

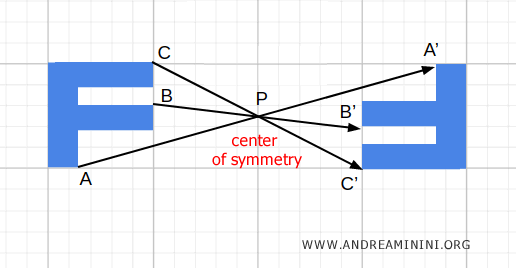
Nota: Otra forma de visualizar la simetría central en el plano es pensarla como una rotación de 180° en torno al centro de simetría P. La figura resultante es una imagen especular congruente a la original, ya que se conservan todas las distancias.

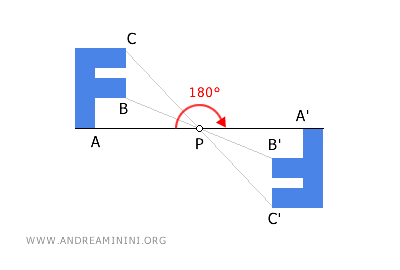
Las figuras obtenidas mediante simetría central siempre son congruentes, ya que mantienen la misma forma y dimensiones, aunque su orientación espacial se invierta.

Dado que preserva las distancias, la simetría central se clasifica como una isometría.

Las ecuaciones

En el plano, la simetría central de un punto P(x;y) con respecto a otro punto C(x₀;y₀), considerado como centro de simetría, se determina mediante las siguientes fórmulas:

$$ \begin{cases} x' = 2x_0 - x \\ \\ y' = 2y_0 - y \end{cases} $$

Nota: Si el centro de simetría coincide con el origen del sistema de coordenadas cartesianas O(0;0), la simetría central se obtiene simplemente invirtiendo el signo de las coordenadas de cada punto. En este caso, x₀=0 e y₀=0, por lo tanto: $$ \begin{cases} x' = - x \\ \\ y' = - y \end{cases} $$

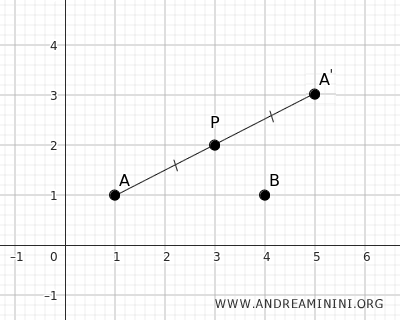
Consideremos ahora como centro de simetría el punto P con coordenadas P(x₀;y₀)=(3;2).

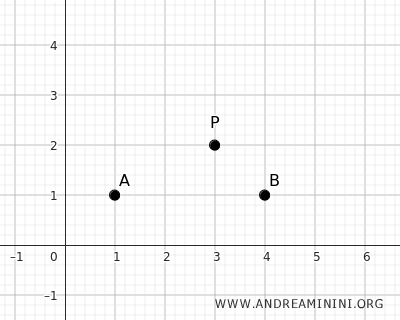
Añadimos dos puntos en el plano: A(1;1) y B(4;1).

Utilizamos las ecuaciones para calcular el punto simétrico A'

El punto A tiene coordenadas x=1 e y=1, mientras que el centro de simetría tiene coordenadas x₀=3 e y₀=2.

$$ \begin{cases} x' = 2x_0 - x \\ \\ y' = 2y_0 - y \end{cases} $$

$$ \begin{cases} x' = 6 - 1 \\ \\ y' = 4 - 1 \end{cases} $$

$$ \begin{cases} x' = 5 \\ \\ y' = 3 \end{cases} $$

Por tanto, el punto simétrico A' tiene coordenadas x'=5 e y'=3.

El punto P es el punto medio del segmento AA'.

Ahora calculemos el punto simétrico B'

El punto B se encuentra en x=4 e y=1, y el centro de simetría sigue siendo P(3;2).

$$ \begin{cases} x' = 6 - 4 \\ \\ y' = 4 - 1 \end{cases} $$

$$ \begin{cases} x' = 2 \\ \\ y' = 3 \end{cases} $$

Así, el punto B' tiene coordenadas x'=2 e y'=3.

El punto P es también el punto medio del segmento BB'.

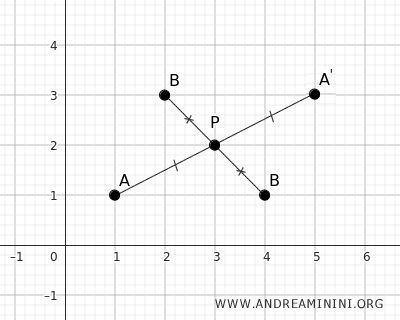
Obsérvese que ambas simetrías pueden interpretarse como rotaciones de 180° de los puntos A y B alrededor del punto P.

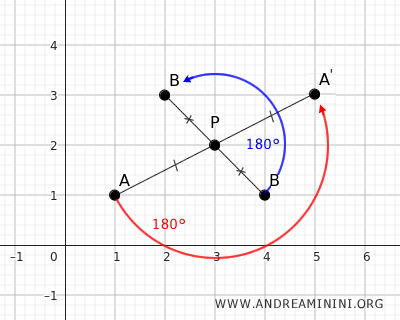
Tras la transformación, la distancia entre los puntos A' y B' permanece inalterada.

Demostración: La simetría central es una transformación geométrica que asocia a cada punto P(x;y) del plano otro punto P'(x';y'), simétrico respecto a un punto M(x_M;y_M) considerado como centro de simetría. Si unimos los puntos P y P' mediante un segmento, el punto M es su punto medio. Por tanto, las coordenadas de M se expresan así: $$ \begin{cases} x_M = \frac{x+x'}{2} \\ \\ y_M = \frac{y+y'}{2} \end{cases} $$ A partir de estas fórmulas se pueden despejar las coordenadas del punto simétrico P': $$ \begin{cases} x' = 2x_M - x \\ \\ y' = 2y_M - y \end{cases} $$ En el caso particular en que el centro de simetría es el origen M(0;0), basta con aplicar: $$ \begin{cases} x' = - x \\ \\ y' = - y \end{cases} $$

Simetría central en el espacio

La simetría central respecto a un punto \( O \) en el espacio es una transformación geométrica que:

• mantiene inalterado el punto \( O \)
• asocia a cada punto \( P \), distinto de \( O \), otro punto \( P' \) tal que \( O \) es el punto medio del segmento \( PP' \), es decir, \( OP \cong OP' \)

A continuación se muestra un ejemplo práctico:

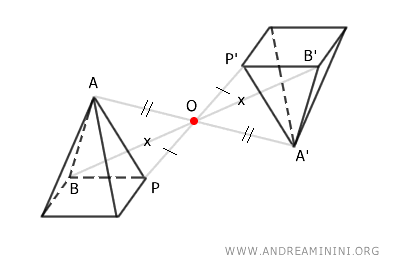
En esta transformación, el punto \( O \) es el único punto fijo; es decir, permanece inalterado.

Dos sólidos relacionados por simetría central respecto a \( O \) son en general congruentes inversos.

Nota: Dos sólidos son congruentes inversos cuando tienen la misma forma y tamaño, pero son imágenes especulares uno del otro. Es decir, no pueden superponerse mediante movimientos rígidos en el espacio sin inversión de orientación.

Funciones con simetría respecto del origen

Una función $f(x)$ presenta simetría respecto del origen si, y solo si, es una función impar, es decir, si cumple que $f(-x) = -f(x)$.

No todas las funciones poseen esta propiedad: la simetría respecto del origen es una característica particular que solo algunas funciones exhiben.

De hecho, la mayoría de las funciones reales no son simétricas ni respecto del eje y (funciones pares), ni respecto del origen (funciones impares).

Nota. Una función es impar si verifica la condición $f(-x) = -f(x)$, y par si se cumple que $f(-x) = f(x)$.

Ejemplo

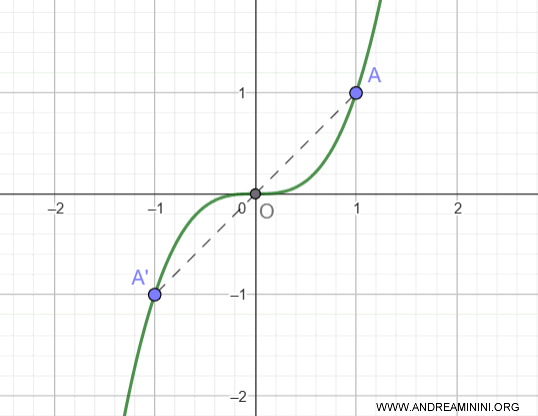
La función $f(x) = x^3$ es impar, ya que:

$$ f(-x) = (-x)^3 = -x^3 = -f(x) $$

Su gráfica es simétrica respecto del origen.

Ejemplo 2

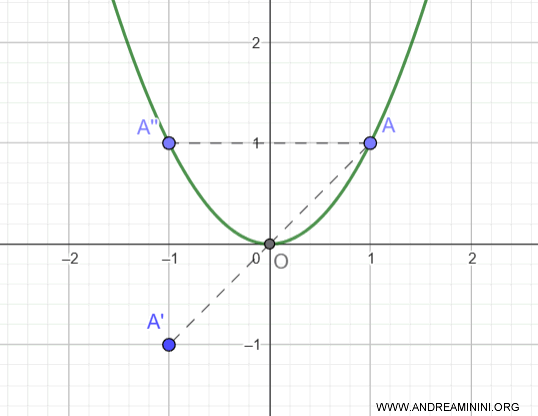
La función $f(x) = x^2$ no es impar.

$$ f(-x) = (-x)^2 = x^2 \ne -f(x) = -x^2 $$

Sin embargo, sí es una función par, ya que es simétrica respecto del eje y:

$$ f(-x) = (-x)^2 = x^2 = f(x) $$

Por lo tanto, no presenta simetría respecto del origen.

Ejemplo 3

La función $f(x) = x + 1$ no es ni par ni impar.

$$ f(-x) = -x + 1 $$

Esta expresión no coincide ni con $f(x) = x + 1$ ni con $-f(x) = -x - 1$, lo cual indica que la función no es simétrica ni respecto del eje y ni respecto del origen.

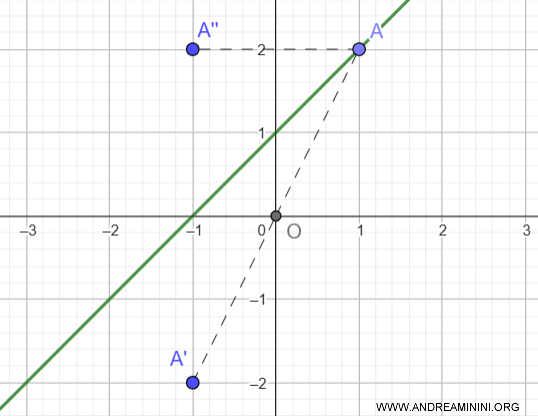
Por tanto, $f(x) = x + 1$ no es par ni impar.

Demostración

Decir que una función es simétrica respecto del origen (0, 0) significa que, si un punto $(x, y)$ pertenece a su gráfica, entonces el punto opuesto $(-x, -y)$ también debe formar parte de ella.

$$ \begin{cases} x' = -x \\ \\ y' = -y \end{cases} $$

Es decir, cualquier punto $(x, f(x))$ de la gráfica, al reflejarse en el origen, se convierte en $(-x, -f(x))$.

Si aplicamos esta simetría a la función $y = f(x)$, obtenemos:

$$ y = -f(-x) $$

Pero como también sabemos que $y = f(x)$, se deduce que:

$$ f(x) = -f(-x) $$

Para que la función permanezca invariante bajo esta simetría, debe cumplirse que $f(x) = -f(-x)$.

Si multiplicamos ambos miembros de la ecuación por $-1$, obtenemos:

$$ -f(x) = f(-x) $$

Lo cual equivale a:

$$ f(-x) = -f(x) $$

Esta es, precisamente, la definición de una función impar.

Observaciones clave

A continuación se presentan algunas observaciones fundamentales sobre la simetría central:

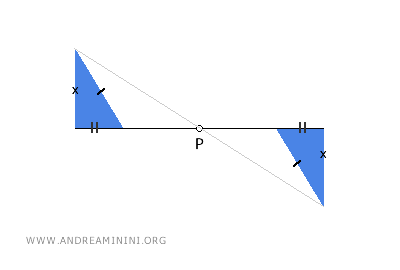
• La figura obtenida mediante simetría central es congruente con la figura original
  La simetría central es una isometría, lo que implica que conserva las distancias entre los puntos de la figura. Como consecuencia, las figuras resultantes tienen lados y ángulos congruentes, por lo que son congruentes entre sí. En este tipo de transformación, la distancia relativa entre puntos permanece invariable.
  
• Invariantes de la simetría central
  La posición del centro de simetría P dentro del plano es un invariante característico de esta transformación. También lo es la dirección de las rectas, así como las distancias relativas entre los puntos de la figura.
• La composición de dos simetrías centrales con el mismo centro equivale a la identidad
  Si se aplican consecutivamente dos simetrías centrales con el mismo centro P, la figura recupera su forma y posición original, como si no hubiese sido transformada. Esta propiedad convierte a la simetría central en una transformación involutiva.
  
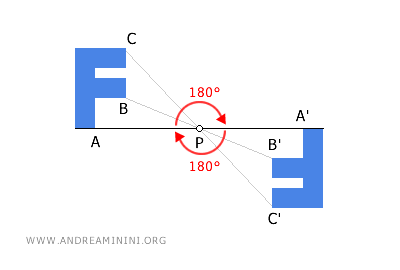
  En general, la composición de un número par de simetrías centrales con un mismo centro siempre da lugar a la transformación identidad.
• La simetría central no es una operación cerrada
  En términos generales, la composición de dos o más simetrías centrales no necesariamente produce otra simetría central. Por tanto, no constituye una operación cerrada. Por ejemplo, la composición de simetrías centrales con centros distintos, como P y P', puede dar lugar a una traslación de la figura. En tal caso, la transformación resultante ya no es una simetría central.
  
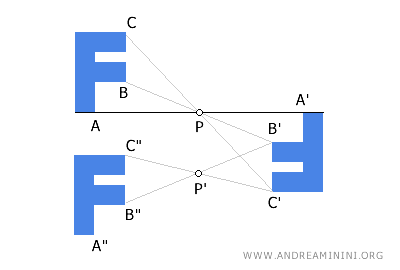
• El centro de simetría es un punto fijo y único
  En una simetría central, el centro de simetría es el único punto que permanece inalterado tras la transformación. Se transforma en sí mismo, lo que lo convierte en un punto fijo (o punto invariante). Esto significa que su posición no cambia, y que además no existe ningún otro punto con esta propiedad.
  
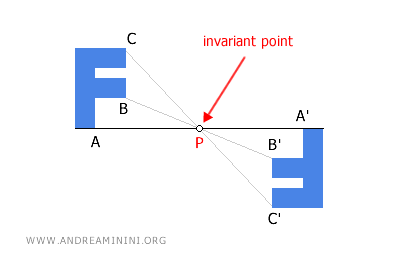
• En la simetría central, las rectas conservan su paralelismo
  Toda recta que se refleja respecto a un centro de simetría tiene por imagen una recta paralela. Por ello, el paralelismo entre rectas es un invariante de esta transformación.
  
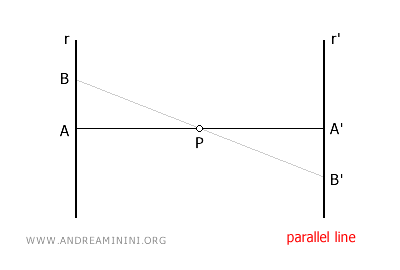
• Toda recta que pasa por el origen es una recta invariante
  En la simetría central, cualquier recta que atraviesa el centro de simetría se transforma en sí misma. A este tipo de recta se la denomina globalmente invariante: la recta en su conjunto permanece inalterada, aunque sus puntos individuales (salvo el propio centro) no queden fijos, sino que se trasladan a nuevas posiciones.
  
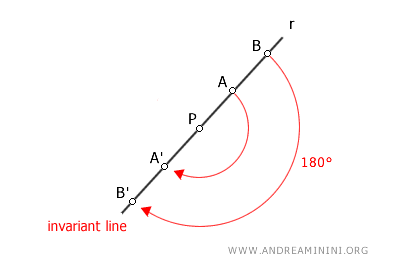
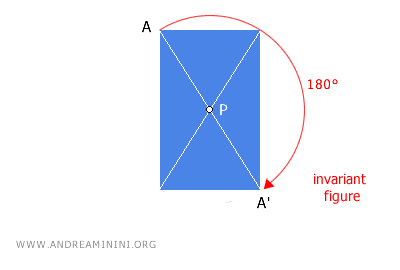
• Centro de simetría de una figura
  Un punto del plano se considera centro de simetría de una figura si, al aplicarle una simetría central con ese punto como centro, la figura resultante coincide exactamente con la original. Es decir, es un punto tal que la figura permanece invariante bajo dicha transformación. Ejemplos típicos de figuras con centro de simetría son el rectángulo, el cuadrado, el rombo, el círculo, entre otros.
  
• La simetría central es una transformación involutiva
  La simetría central, denotada por $ T $, es una transformación involutiva, lo que significa que su inversa $ T^{-1} $ coincide con la propia transformación: $$ T^{-1} = T $$ Por lo tanto: $$ T^{-1} \circ T = T \circ T^{-1} = \text{id} $$ Es decir, aplicar la transformación dos veces equivale a la transformación identidad: todo punto regresa a su posición original. $$ T \circ T = \text{id} $$
• La composición de dos simetrías centrales con centros distintos equivale a una traslación
  Al componer dos simetrías centrales $S_{M_1}$ y $S_{M_2}$, con centros en $M_1$ y $M_2$ respectivamente, se obtiene una transformación equivalente a una traslación cuyo vector tiene una magnitud exactamente igual al doble de la longitud del segmento $ \overline{M_1M_2} $: $$ S_{M_1} \circ S_{M_2} \leftrightarrow \vec{v} = 2\,\overrightarrow{M_1 M_2} $$ 

  Ejemplo. Partimos de un punto $A$, lo reflejamos respecto a $M_1$ y obtenemos el punto $B$. A continuación, reflejamos $B$ respecto a $M_2$, obteniendo así el punto $C$.
  
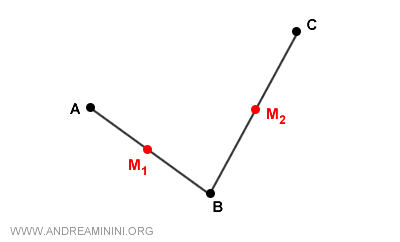
  En realidad, el desplazamiento de $A$ a $B$ y luego de $B$ a $C$ produce exactamente el mismo resultado que trasladar directamente $A$ hasta $C$. Esta traslación está representada por el vector $  \vec{v} = 2\,\overrightarrow{M_1 M_2} $, cuya longitud es el doble de la del segmento que une los puntos medios $M_1$ y $M_2$, y cuya dirección coincide con la de dicho segmento.
  
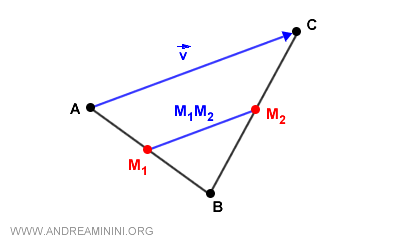
  Demostración. El vector $ \vec{v} = 2\,\overrightarrow{M_1 M_2} $ tiene una magnitud igual al doble de la longitud de $\overline{M_1 M_2}$ porque los puntos $A$, $B$ y $C$ forman un triángulo $ABC$ en el que $M_1$ y $M_2$ son los puntos medios de los lados $AB$ y $BC$, respectivamente. De acuerdo con el teorema del segmento medio, el segmento $\overline{M_1 M_2}$, que une los puntos medios de dos lados ($AB$ y $BC$), es paralelo y mide exactamente la mitad del lado restante ($AC$) del triángulo. Esto confirma que el vector de traslación $\vec{v}$ es siempre el doble de largo que $\overline{M_1 M_2}$ y mantiene la misma dirección.

Y así sucesivamente.