Reflexión deslizante
Una reflexión deslizante es una transformación geométrica del plano que combina una reflexión respecto de una recta $r$ con una traslación $T_{\vec{v}}$ definida por un vector $\vec{v}$ paralelo a dicha recta. $$ G = T_{\vec{v}} \circ S_r $$
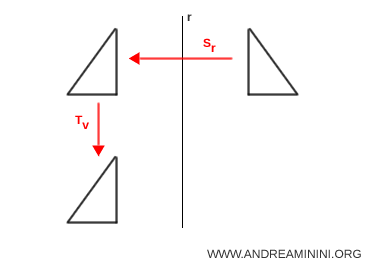
La reflexión deslizante es una isometría, lo que significa que conserva las distancias entre los puntos.
No obstante, no puede reducirse a ninguna de las transformaciones elementales por separado.
No es una reflexión pura, porque ninguna recta permanece fija punto por punto: todos los puntos del plano resultan desplazados.
Tampoco es una simple traslación, ya que la reflexión invierte necesariamente la orientación de la figura.
Nota. Existen dos casos particulares: si el vector de traslación es nulo ($\vec{v}=0$), la reflexión deslizante se reduce a una reflexión. Si se omite la reflexión, lo que queda es simplemente una traslación.
Un ejemplo ilustrativo
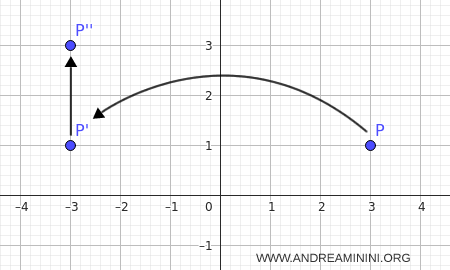
Consideremos el plano cartesiano, una reflexión y una traslación:
- La reflexión es respecto de la recta $r: x=0$, es decir, el eje $y$.
- La traslación está definida por el vector $\vec{v} = (0,2)$, paralelo a $r$.
Tomemos el punto $P(3,1)$.
Al reflejarlo respecto de $r$, obtenemos $P'(-3,1)$.
Aplicando después la traslación $\vec{v}$, resulta $P''=(-3,1+2) = (-3,3)$.
Así, bajo la reflexión deslizante, el punto $P$ se transforma en $P''$.
Geométricamente, una reflexión deslizante puede interpretarse como un “deslizamiento reflejado”: primero se refleja la figura respecto de una recta y, a continuación, se la desplaza a lo largo de dicha recta.
Observaciones adicionales
Algunas consideraciones sobre las reflexiones deslizantes:
- Ausencia de puntos fijos
A diferencia de una reflexión, en la que los puntos del eje permanecen invariantes, una reflexión deslizante no deja ningún punto fijo. Todos los puntos del plano se desplazan. El único elemento que se conserva globalmente es el eje de reflexión, que se mapea sobre sí mismo, aunque ninguno de sus puntos permanezca inalterado.
Y así sucesivamente.